微积分在神经网络中的本质
calculus
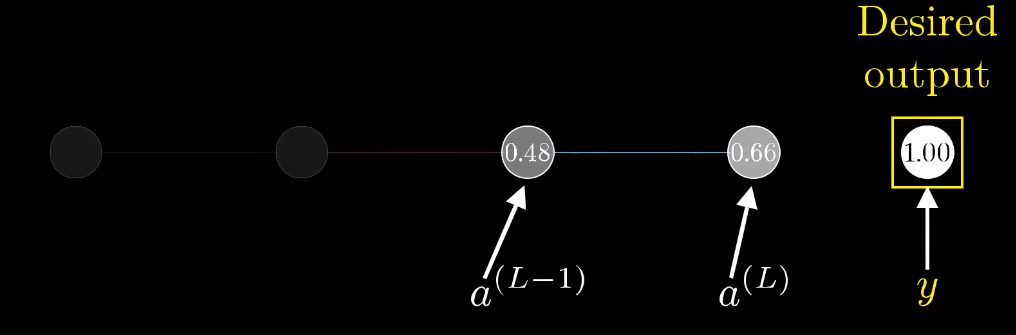
在一个神经网络中我们通常将每一层的输出结果表示为: a [ l ] a^{[l]} a[l]
[ 1 ] [1] [1]
对应的计算记录为为:
a
[
l
]
:
第
l
层
a
[
j
]
:
第
j
个神经元
a^{[l]}:\textcolor{red}{第l层}\\ a_{[j]}:\textcolor{green}{第j个神经元}\\
a[l]:第l层a[j]:第j个神经元
代价函数为:

其中y为实际值,
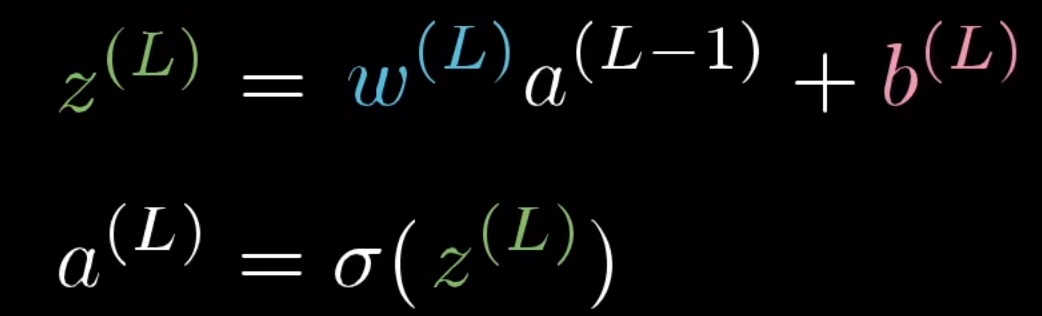
而对于 d C 0 d w {d{C_0}\over dw} dwdC0是求斜率,或者具体的解释是 w \textcolor{green}{w} w的数值变动对 C 0 \textcolor{red}{C_0} C0的影响:
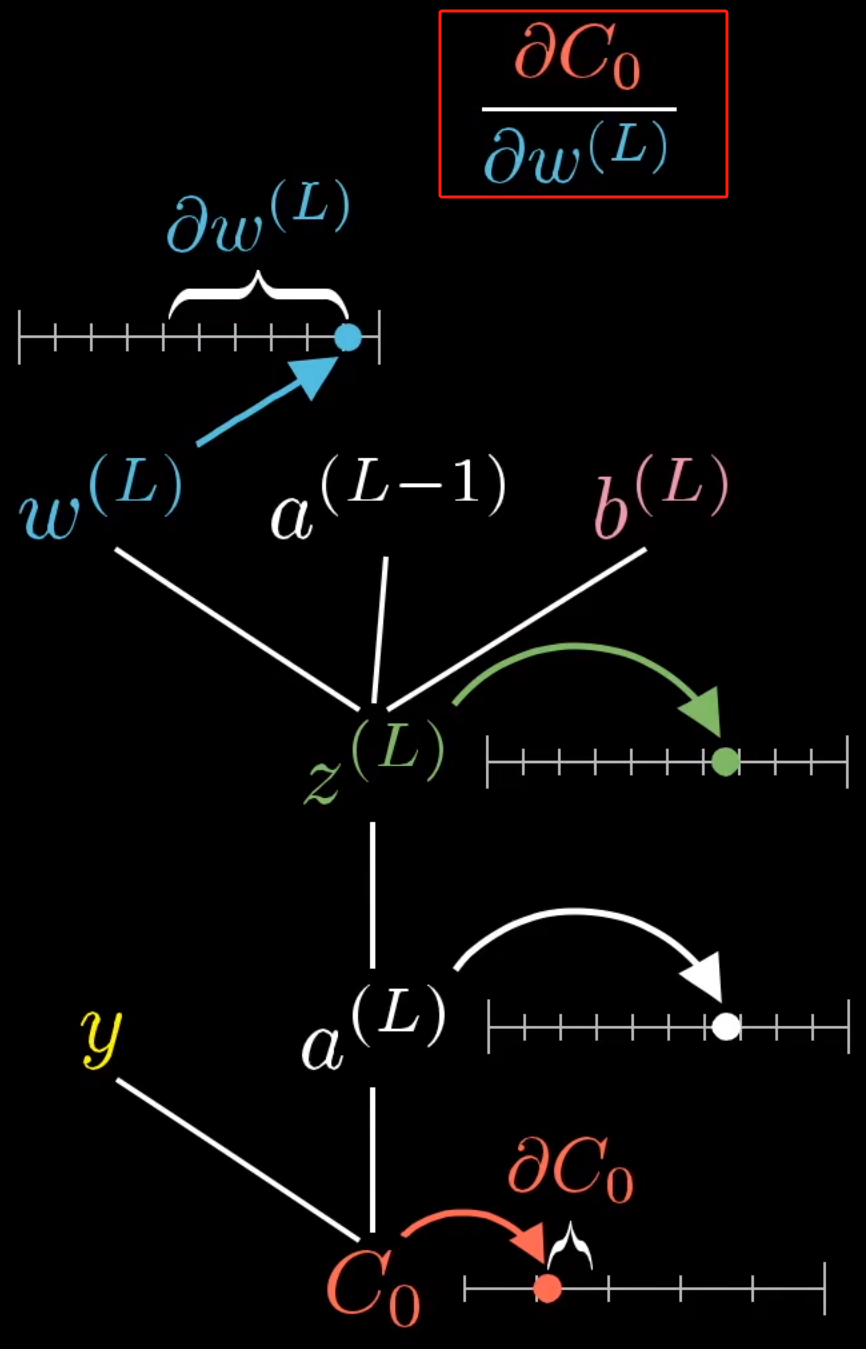
根据链式法则:
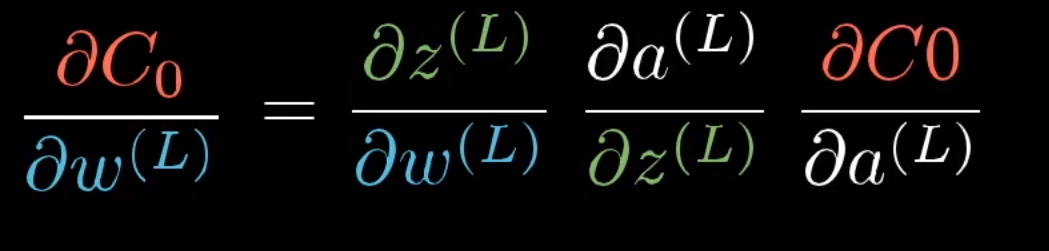
具体计算过程:
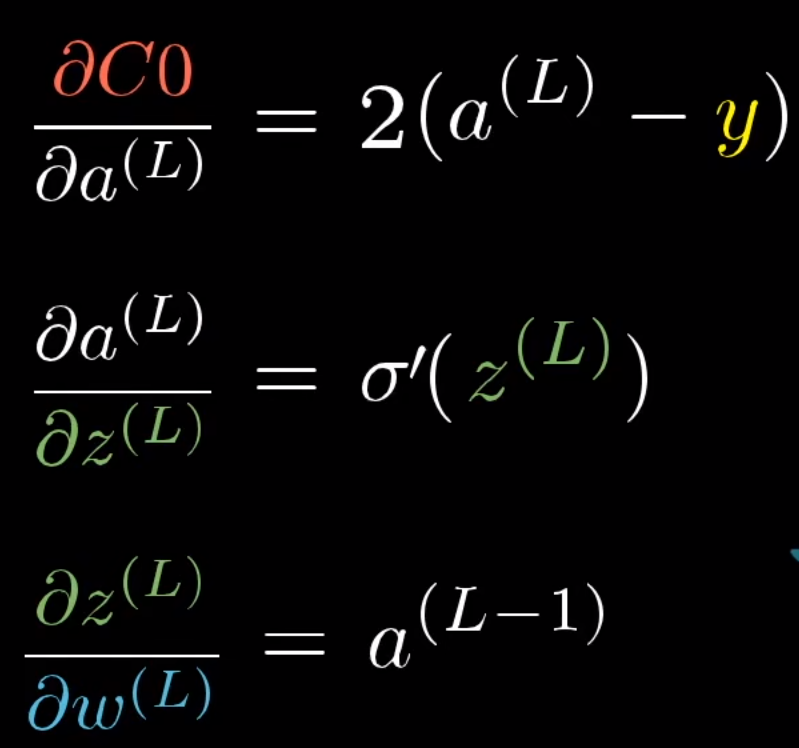
所以 w \textcolor{green}{w} w的数值变动对 C 0 \textcolor{red}{C_0} C0的影响与:真实值与计算值的偏差、激活函数 σ \sigma σ,上一层的输出值有关
如果理解了上述的内容,其他的代价函数 ∇ C \nabla C ∇C就只是换偏导对象即可:
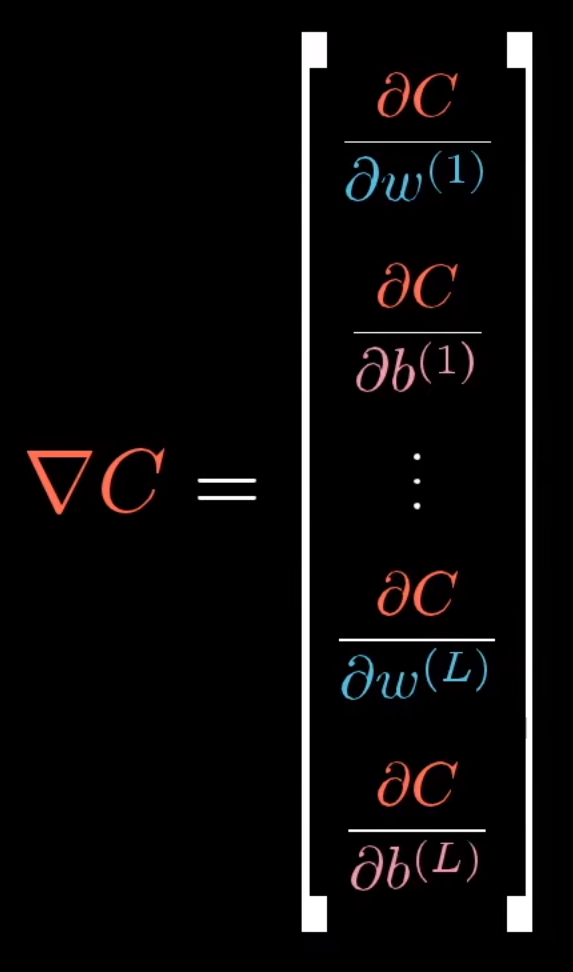
比如,如果要计算 d C 0 d b {d{C_0}\over db} dbdC0,只需要替换一项即可:
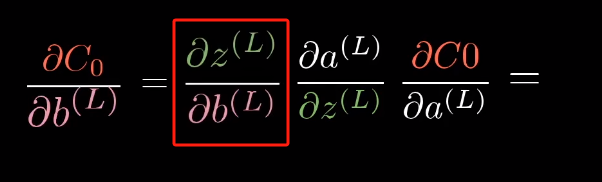
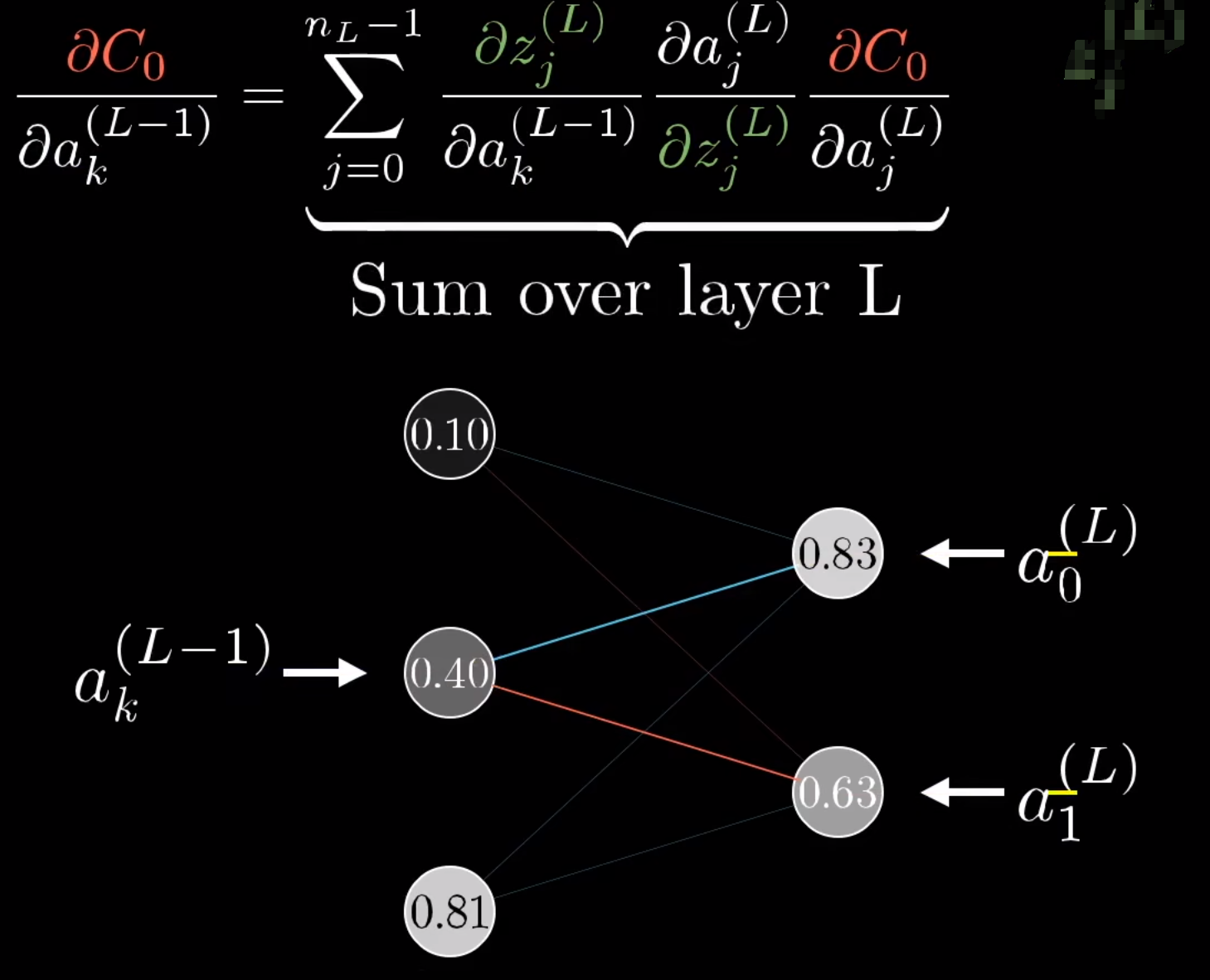
同理,应用在BP中可以计算 w j k L ; 一条线的权值的影响 w^{L}_{jk}\textcolor{red}{;一条线的权值的影响} wjkL;一条线的权值的影响(其中jk分别代表 L − 1 L-1 L−1和 L L L层中的不同点):
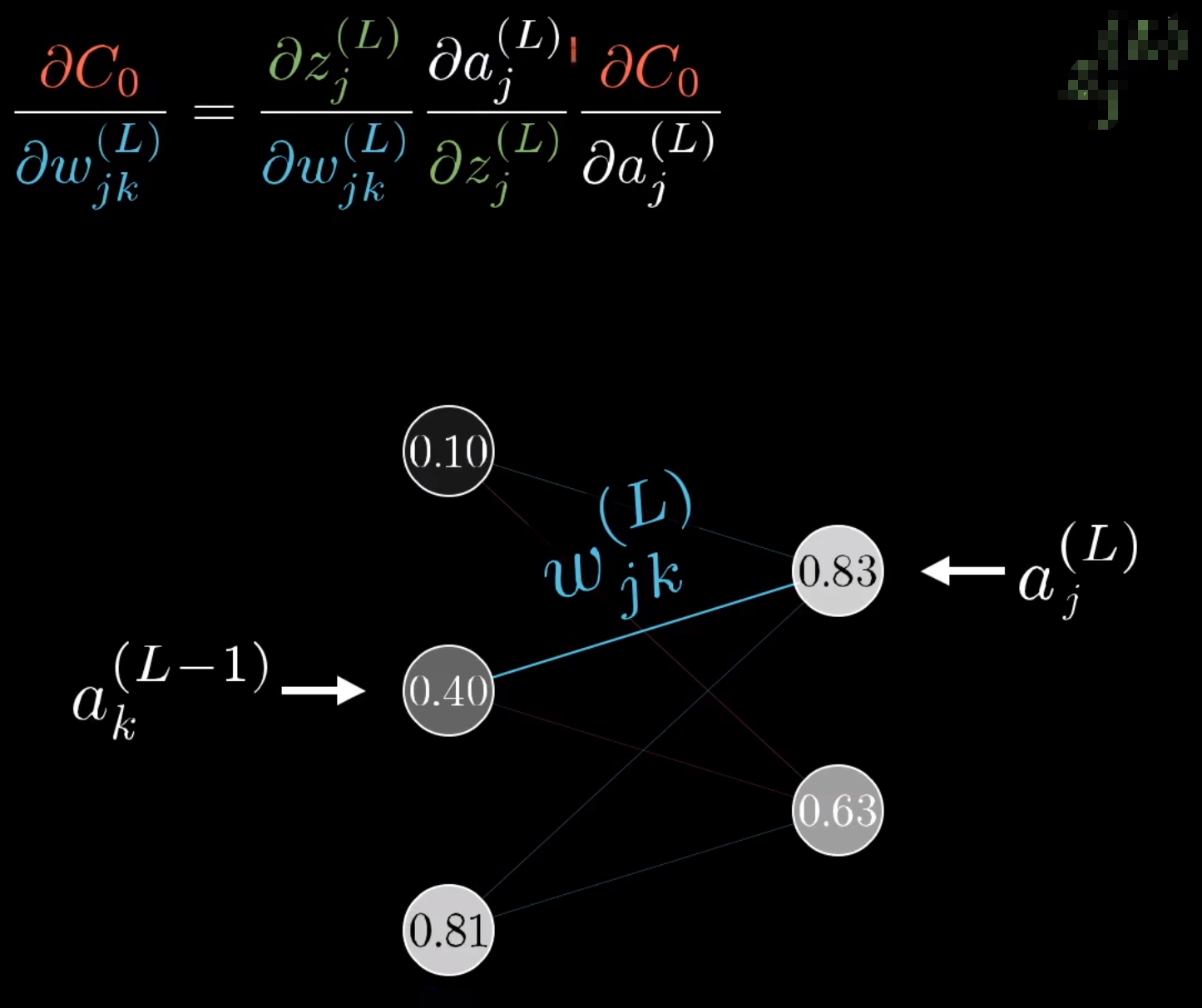
也可以计算 a k L − 1 ; 前一层的输出值的影响 a^{L-1}_{k}\textcolor{red}{;前一层的输出值的影响} akL−1;前一层的输出值的影响: