算法设计与分析复习--贪心（一）

上一篇

算法设计与分析复习–动态规划

贪心的性质

贪心和动态规划都要求问题具有最优子结构；
可用贪心方法时，动态规划可能不适用
可用动态规划方法时，贪心方法可能不适用

活动安排问题

AcWing 908. 最大不相交区间数量

产生最优解的排序是按照结束时间从小到大排序，看不重合区间的数量

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<int, int> PII;//使用pair存储一个时间段
const int N = 100010;

int n;
vector<PII> a;

bool cmp(PII x, PII y)
{
    return x.second < y.second;//结束时间小的排前面
}

int main()
{
    scanf("%d", &n);
    
    for (int i = 0; i < n; i ++)
    {
        int l, r;
        scanf("%d%d", &l, &r);
        a.push_back({l, r});
    }
    
    sort(a.begin(), a.end(), cmp);// 按结束时间进行先后排序
    
    int res = 1, ed = a[0].second;
    for (auto i : a)
    {
        if (i.first > ed){//不重合就加上，更新ed
            res ++;
            ed = i.second;
        }
    }
    printf("%d", res);
    return 0;
}

贪心背包问题

与一般的背包问题不一样，开始给出的是整个物品的重量和价值，但是可以只放这个物品的一部分=>贪心背包

按单价排序是贪心背包的解决方法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

typedef pair<double, double> PII;//存在小数情况都要改成double类型
const int N = 1010;

int n, c;
double w[N], v[N];
vector<PII> ob;

bool cmp(PII x, PII y)
{
    return (x.second / x.first) > (y.second / y.first); 
}

int main()
{
    scanf("%d%d", &n, &c);
    
    for (int i = 0; i < n; i ++) scanf("%lf", &w[i]); // 读取为double类型
    for (int i = 0; i < n; i ++) scanf("%lf", &v[i]); // 读取为double类型
    for (int i = 0; i < n; i ++) ob.push_back({w[i], v[i]});
    
    sort(ob.begin(), ob.end(), cmp);
    
    double bv = 0, cw = 0;
    for (auto i : ob)
    {
        cw += i.first;
        if (cw > c){
            bv += (c - (cw - i.first)) * (i.second / i.first); // 把之前加上的i.first要先减掉
            break;
        }
        bv += i.second;
    }
    
    printf("%.2lf", bv); // 输出精度为两位小数
    return 0;
}

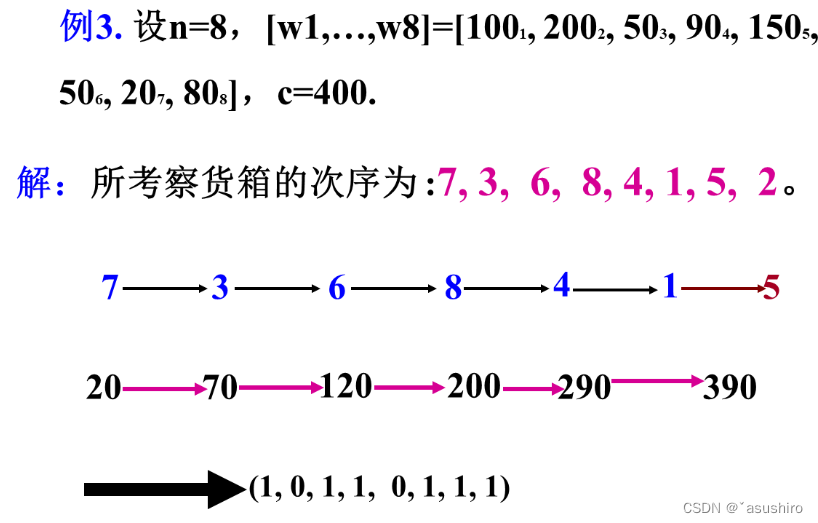
最优装载

贪心选择策略：重量最轻者优先装载

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;
typedef pair<int, int> PII;

const int N = 100010;

int n, c, x[N], cc;
vector<PII> ob;

int main()
{
    scanf("%d%d", &n, &c);
    for (int i = 0; i < n; i ++)
    {
        int w;
        scanf("%d", &w);
        ob.push_back({w, i});
    }
    
    sort(ob.begin(), ob.end());
    
    int res = 0;
    for (auto i : ob)
    {
        cc += i.first;
        if (cc <= c){
            res ++;
            x[i.second] = 1;
        }
        else{
            x[i.second] = 0;   
        }
    }
    
    printf("%d\n", res);
    for(int i = 0; i < n; i ++) printf("%d ", x[i]);
    return 0;
}

下一篇

算法设计与分析复习–贪心（二）