图像处理01 小波变换
一.为什么需要离散小波变换
连续小波分解,通过改变分析窗口大小,在时域上移动窗口和基信号相乘,最后在全时域上整合。通过离散化连续小波分解可以得到伪离散小波分解, 这种离散化带有大量冗余信息且计算成本较高。
小波变换的公式如下:
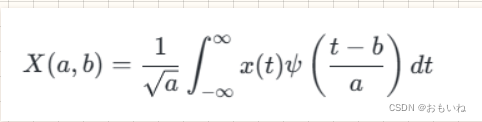
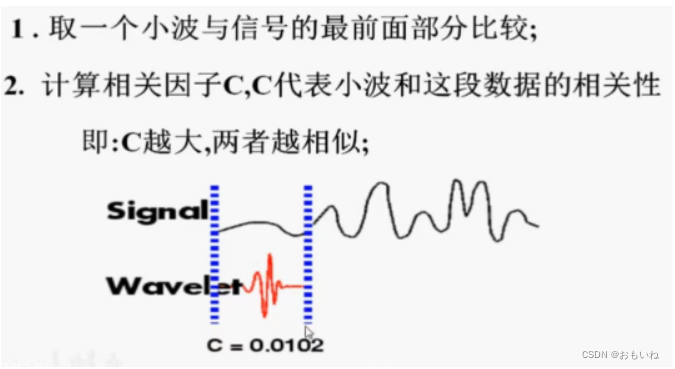
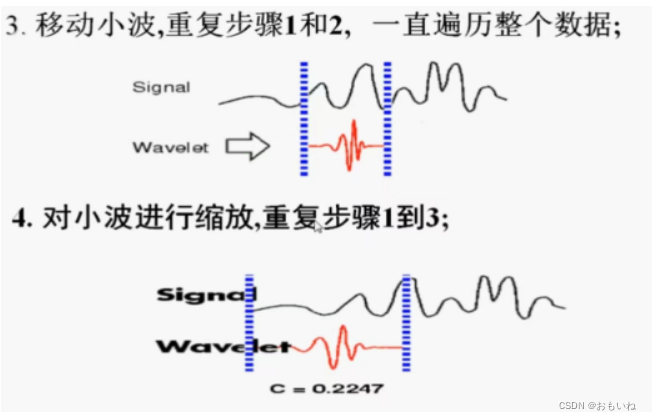
通过下面步骤即可得到不同尺度下的小波变换。
二.离散小波变换
我们将小波的尺度和平移参数以2的指数幂的形式进行变换,我们可以得到一串不同的小波。这些子小波的尺度参数以2的j次方的形式增长。当使用这一系列的子小波,对一个连续函数进行离散分析时,我们所获得的是一组小波分析的系数,这个分析过程称为**小波系列分解**。
而高尺度小波代表着低频信息,小尺度的小波代表着高频信息。
因此如下图所示,不同尺度的小波来实现频率上的覆盖。
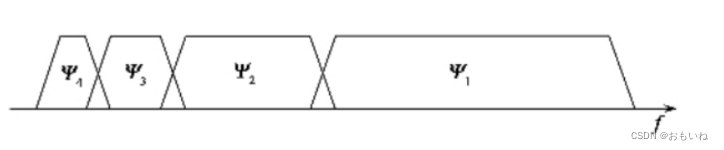
因此我们可以理解,为什么离散小波变换可以等效为通过一个高通和低通滤波器。
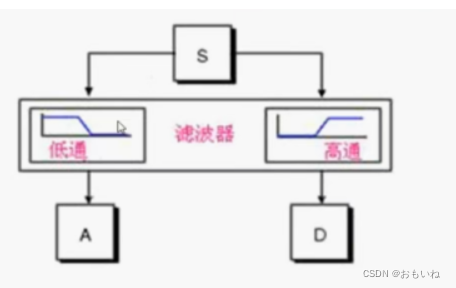
更直观的可以用下面的图片来表示。
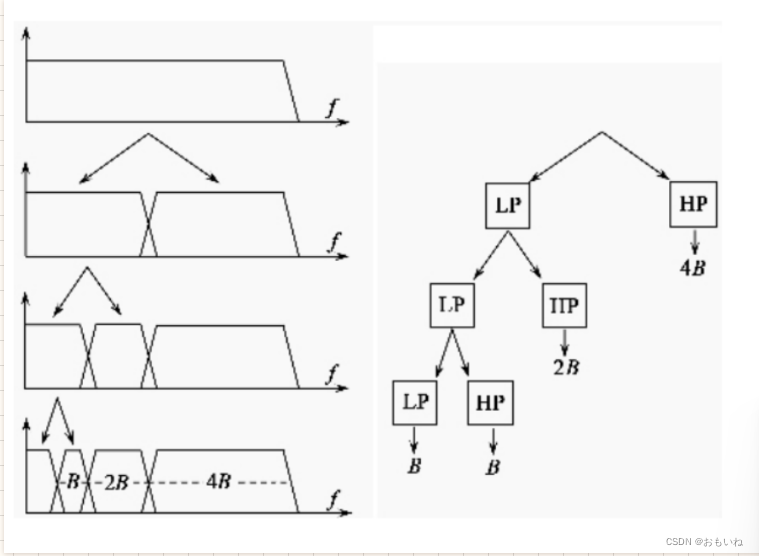
三.直观意义
当我们懂了上面的内容,再来看看小波变换的过程,是否能有了以下体会。
小波分解的多尺度可以类比为我们使用不同的“放大镜”去观察一个物体。想象一下你手里有一张非常复杂的画,画面上有大的物体,如山脉、树木,但也有非常细小的细节,如叶子上的纹理或昆虫的触角。
粗尺度(低分辨率) :当你使用低倍的放大镜(或者站得很远)去看这幅画时,你可以看到大的物体,如山脉和树木,但可能看不到细小的纹理或昆虫。在小波分解中,这就像我们查看信号的低频部分,捕获其主要的、宽泛的特征。
细尺度(高分辨率) :现在,如果你换一个高倍的放大镜(或者走近一些)去看同一幅画,你可能会失去对整体的感知,但可以清晰地看到叶子上的纹理或昆虫的触角等细节。在小波分解中,这就像我们查看信号的高频部分,捕获其细节和快速的变化。
小波分解的美妙之处在于,它同时提供了多个尺度的视角,让我们既可以看到信号的整体特征,又可以看到其细节。这就像我们可以同时拥有多个不同倍率的放大镜,让我们在需要的时候选择合适的一个来观察画面。
四.小波变换实现分解和重构。
如图a是带有噪声的信号,经过4层小波变换得到的变换后的先后如下。
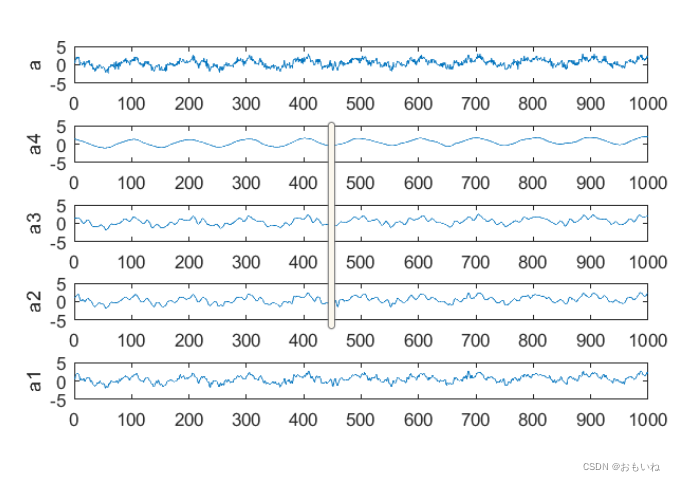
代码如下所示:
%% 1.生成仿真信号
Fs = 1000; % 采样频率
t = 0:1/Fs:1-1/Fs; % 时间向量
% 创建一个合成信号:包含不同频率的正弦波、趋势和噪声
signal = cos(2*pi*10*t) + 0.5*sin(2*pi*50*t) + t + 0.5*randn(size(t));
figure('color','white')
subplot(3,2,1)
%% 2.绘制DWT分解图
subplot(6,1,1);
plot(signal)
ylabel(['a']);
[C,L] = wavedec(signal,4,waveletType);
for i=1:4
a = wrcoef('a',C,L,waveletType,5-i);
subplot(6,1,i+1);
plot(a);
ylabel(['a',num2str(5-i)]);
end
