当前位置： 首页 > article >正文

数据结构之链表练习与习题详细解析

article 2024/12/25 9:35:09

个人主页：点我进入主页

专栏分类：C语言初阶      C语言程序设计————KTV       C语言小游戏     C语言进阶

C语言刷题       数据结构初阶

欢迎大家点赞，评论，收藏。

一起努力，一起奔赴大厂。

目录

1.前言

2.习题解析

2.1习题一

2.2习题二

2.3习题三

2.4习题四

2.5习题五

3.总结

1.前言

        在上次的文章中我们对一些练习的题目进行解析 ，链表是对于数据结构的基础，对我们的后面的内容非常重要，这次我们对于牛客网和力扣的部分题目进行练习 ，这次的题目相对于上次的习题有一些强度，我们可以先自己练习练习让后再看后面的解析

习题一：链表的回文结构

习题二：输入两个链表，找出它们的第一个公共结点

习题三：给定一个链表，判断链表中是否有环

习题四：给定一个链表，返回链表开始入环的第一个节点。 如果链表无环，则返回 NULL

习题五:给定一个链表，每个节点包含一个额外增加的随机指针，该指针可以指向链表中的任何节点或空节点。要求返回这个链表的深度拷贝

2.习题解析

2.1习题一

        对于一个链表，请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法，判断其是否为回文结构。给定一个链表的头指针A，请返回一个bool值，代表其是否为回文结构。保证链表长度小于等于900。

测试样例：

1->2->2->1

返回 true

class PalindromeList {
  public:
    bool chkPalindrome(ListNode* head) {
        // write code here
        struct ListNode* phead = (ListNode*)malloc(sizeof(ListNode));
        struct ListNode* s = phead, *s1 = head;
        struct ListNode *tail;
        phead->next = NULL;
        struct ListNode* slow = head;
        struct ListNode* fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        while (slow) { 
            tail=slow->next;
            slow->next = s->next;
            s->next = slow;
            slow = tail;
        }
        s = s->next;
        while (s&&s1) {
            if (s->val != s1->val)
                return false;
            s = s->next;
            s1 = s1->next;
        }
        return true;
    }
};

        在这里我们可以用到快慢指针，我们可以对几种情况进行判断，空链表，单个节点，奇数个节点的链表，偶数个节点的链表这几种情况，我们可以创建一个头节点进行解题，我们先看奇数个几点的链表和偶数个节点的链表，例如5个或6个节点

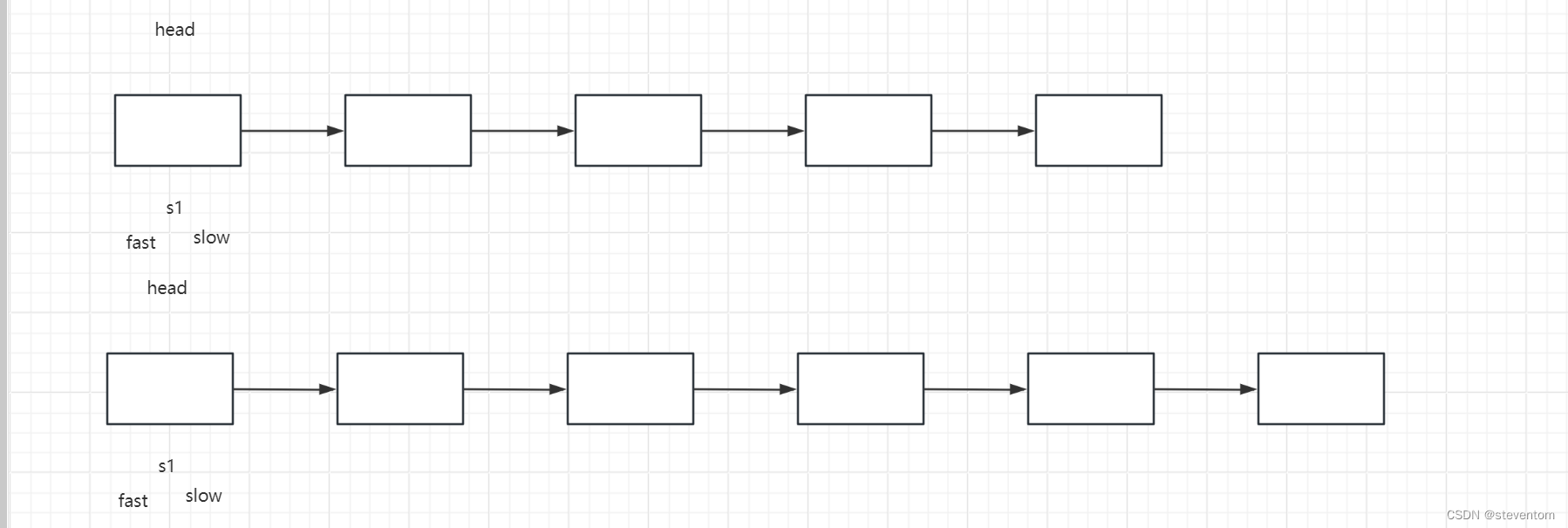
我们让慢指针每次走一次，快指针每次走两次

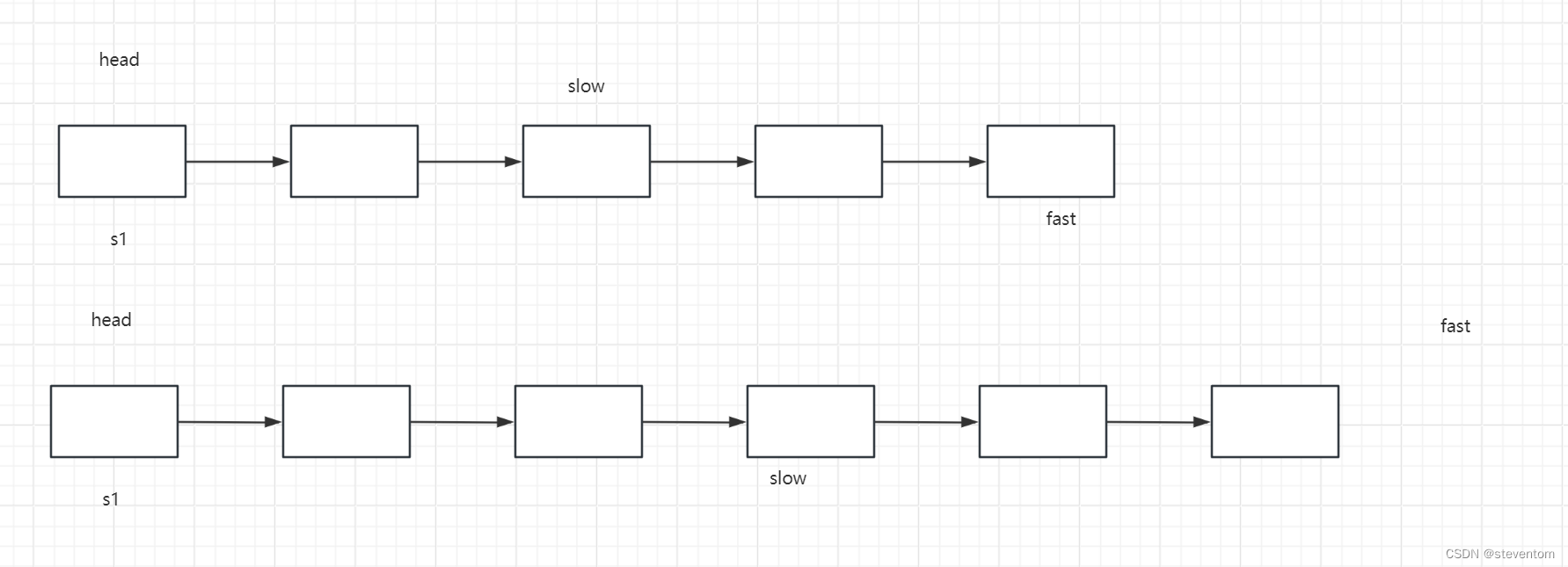
当慢指针在中间的位置时当有奇数个节点时fast->next为NULL，偶数个节点时fast为NULL ，因此我们想要找到中间节点可以利用while循环来找到中间节点，找到中间节点后我们需要对数据进行比对来判断是不是回文结构如果是回文结构数据就是逆置的，因此我们可以想到对链表进行逆置，我们知道头插会将数据逆置，因此我们可以利用头插将数据进行逆置，我们创建一个头节点用于链表的逆置，逆置完成后我们进行数据的比对，当有一个节点时

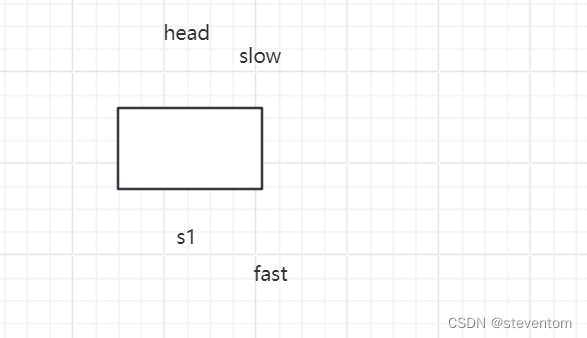
我们看到当找中间节点时由于fast->next为NULL，会直接停止，空链表和这个相同，这俩不用格外考虑。

2.2习题二

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

图示两个链表在节点 c1 开始相交：

题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：

评测系统 的输入如下（你设计的程序 不适用 此输入）：

  • intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
  • listA - 第一个链表
  • listB - 第二个链表
  • skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
  • skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数

评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

 

示例 1：

输入：intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3
输出：Intersected at '8'
解释：相交节点的值为 8 （注意，如果两个链表相交则不能为 0）。
从各自的表头开始算起，链表 A 为 [4,1,8,4,5]，链表 B 为 [5,6,1,8,4,5]。
在 A 中，相交节点前有 2 个节点；在 B 中，相交节点前有 3 个节点。
— 请注意相交节点的值不为 1，因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说，它们在内存中指向两个不同的位置，而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点，B 中第四个节点) 在内存中指向相同的位置。
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode*list1=headA,*list2=headB;
    int counta=0,countb=0;
    while(list1)
    {
        counta++;
        list1=list1->next;
    }
    while(list2)
    {
        countb++;
        list2=list2->next;
    }
    int def=abs(counta-countb);
    struct listNode*longList=headA,*slowList=headB;
    if(counta<countb)
    {
        longList=headB;
        slowList=headA;
    }
    list1=longList;
    list2=slowList;
    while(def--)
    {
        list1=list1->next;
    }
    while(list1&&list2&&(list1!=list2))
    {
        list1=list1->next;
        list2=list2->next;
    }
    if(list1==NULL||list2==NULL)
        return NULL;
    else 
        return list1;

}

        我们可以先得到链表A的长度和链表B的长度，然后找到两个链表节点的差值，然后让长的链表先走差值个节点，然后让两个指针分别指向两个链表，我们用到一个非常好的方法，我们假设长的先指向A,短的指向B,然后比较A的节点数和B的节点数，然后进行修正，然后对长的指针和短的指针进行操作即可，让他们同时走，比较这两个指针的地址（必须是地址），当相同且不为NULL时返回。

2.3习题三

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例 1：

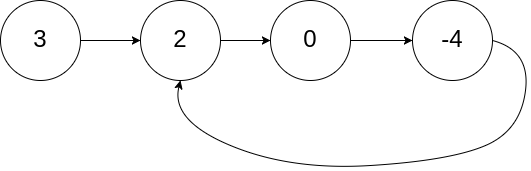
输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

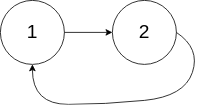
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。
bool hasCycle(struct ListNode *head) {
    struct ListNode*fast=head,*slow=head;
    if(fast==NULL||fast->next==NULL)
    {
        return false;
    }
    slow=slow->next;
    fast=fast->next->next;
    while(slow!=fast)
    {
        if(fast==NULL||fast->next==NULL)
        {
          return false;
        }
        slow=slow->next;
        fast=fast->next->next;
    }
    return true;
}

 在这里我们可以想到主要有两种情况的链表

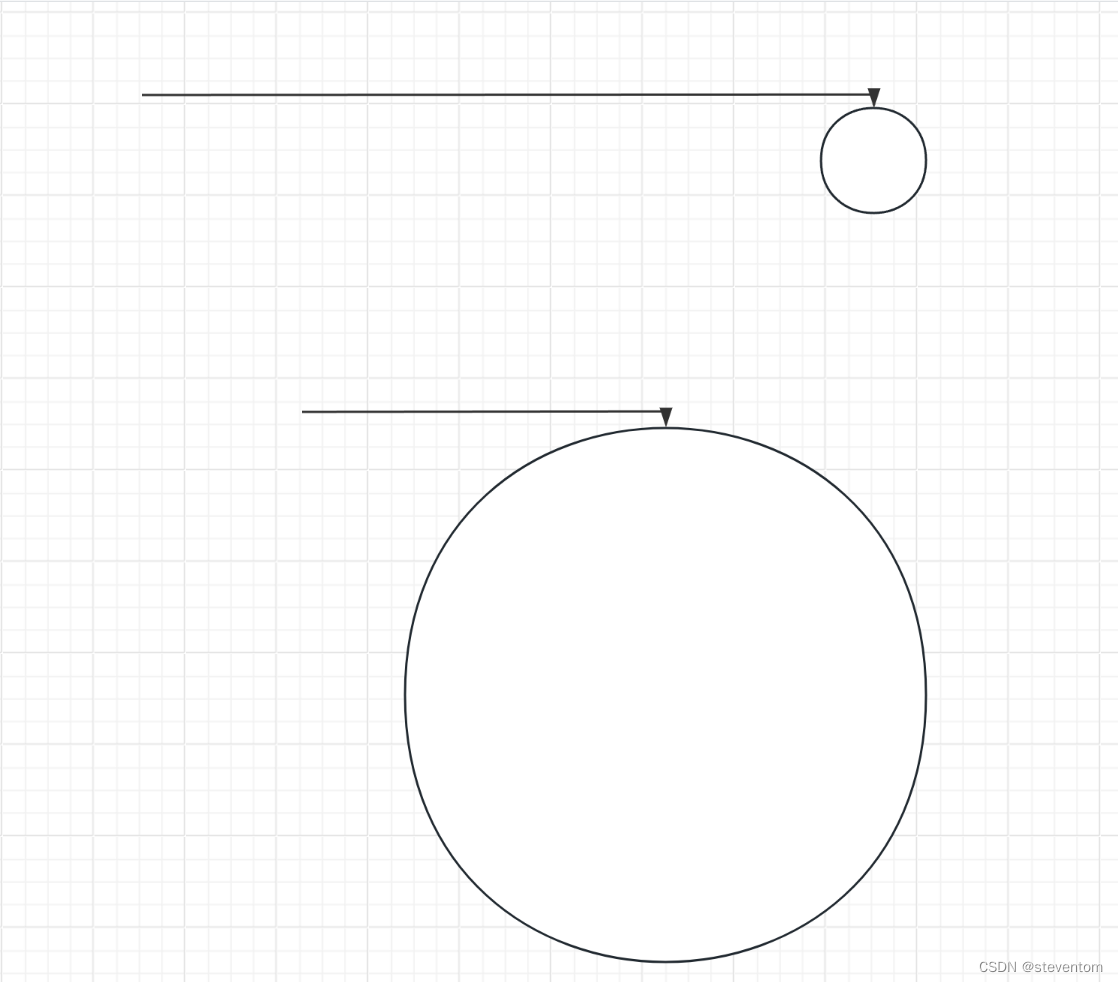
分别为环长和环短的两种，我们可以搞快慢指针进行操作，快指针每次走两次，慢指针每次走一次，

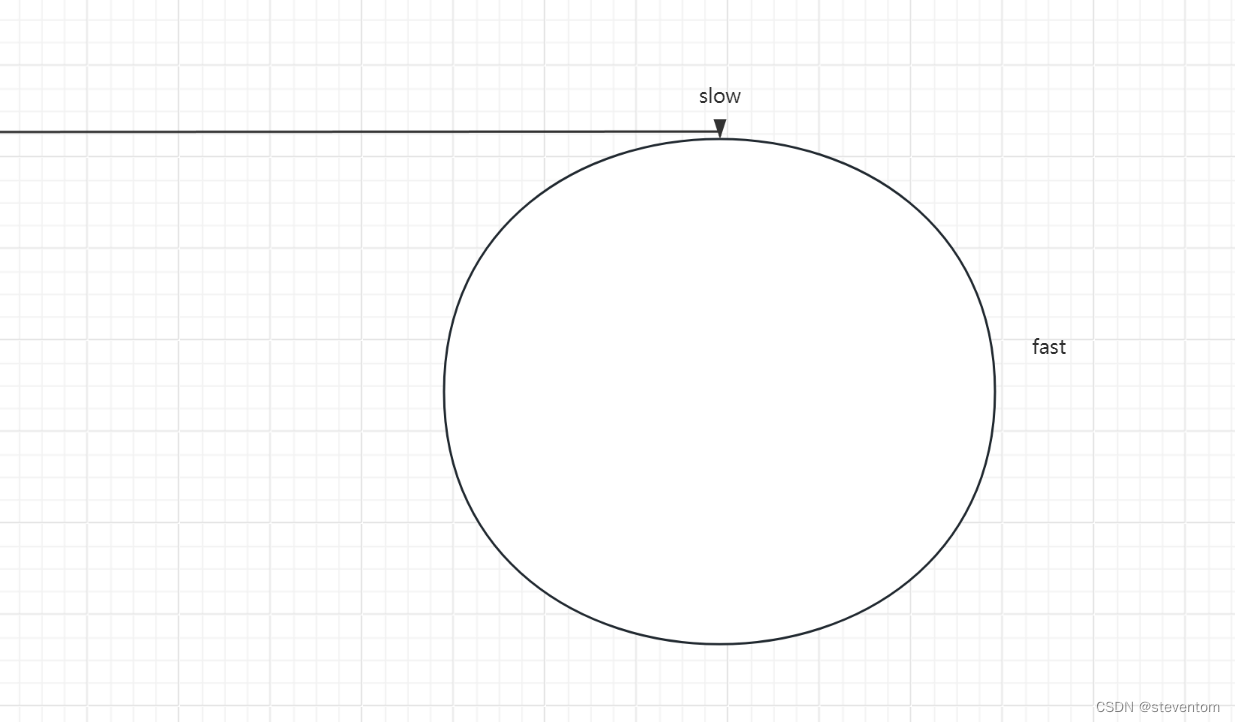
当慢指针指向环的开始时由于快指针每次走两次，满指针每次走一次，我们看快指针相对于慢指针每次走一次，那么 快指针一定会和慢指针相遇，那么我们先进行判断是不是空，然后快慢指针进行走，然后进行循环，进行判断，对于快慢指针的走法我们想到快指针走三次，慢指针走一次能不能成功，快指针每次走m次，慢指针每次走n次是否可以，我们先对于快指针走三次，慢指针走一次，慢指针走到环的开始位置，当快指针和慢指针差奇数个时第二次相遇可以，当差偶数个时此一次相遇即可，当快指针每次走m次，慢指针每次走n次时

我们设环外为L,环长为C，slow和fast的差距为x，我们可以得到公式：m(L+x)=n(L+kC+X),我们可以化简为（m-n）L=kLC+(n-m)X,L=kLC/(m-n)-X;我们根据公式可以得到需要满足m>n才有可能相遇。

2.4习题四

给定一个链表的头节点  head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

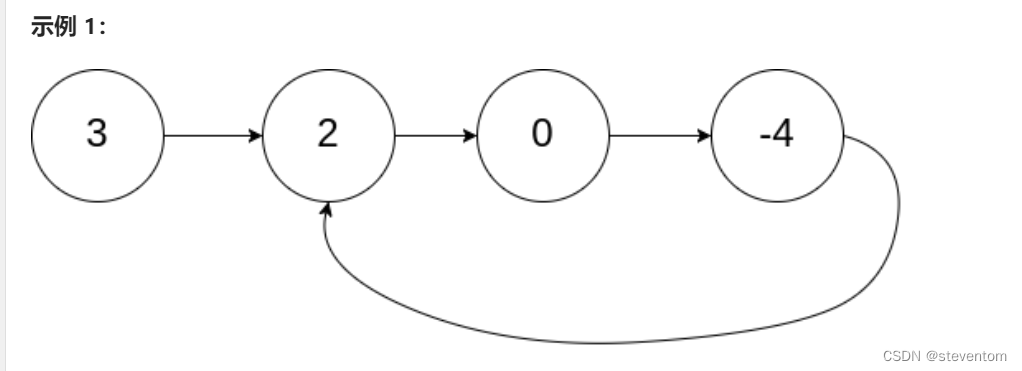
输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。
struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *slow=head;
    struct ListNode *fast=head;
    if(fast==NULL||fast->next==NULL)
        return NULL;
        slow=slow->next;
    fast=fast->next->next;
    while(slow!=fast)
    {
   if(fast==NULL||fast->next==NULL)
        return NULL;
        slow=slow->next;
        fast=fast->next->next;
    }
    slow=head;
    while(slow!=fast)
    {
        slow=slow->next;
        fast=fast->next;
    }
    return fast;
}

        根据上面一道题目我们可以来判断有没有环，我们还得到一个公式 ,L=kC/(m-n)-X;我们先看快指针走两次，慢指针走一步。2(L+x)=kC+x+L，L=(k-1)C+C-x，重点就在C-x这里C-x

我们让慢指针指向头节点， 快指针不变，然后让快慢指针每次走1次，（k-1）C是整圈，再走C-x刚好可以和慢指针在环的位置相遇。对于快指针走3次慢指针走1次，3(L+x)=L+kC+x ,L=aC+C-x，和上面相同可以相遇。

2.5习题五

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为  null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

示例 1：

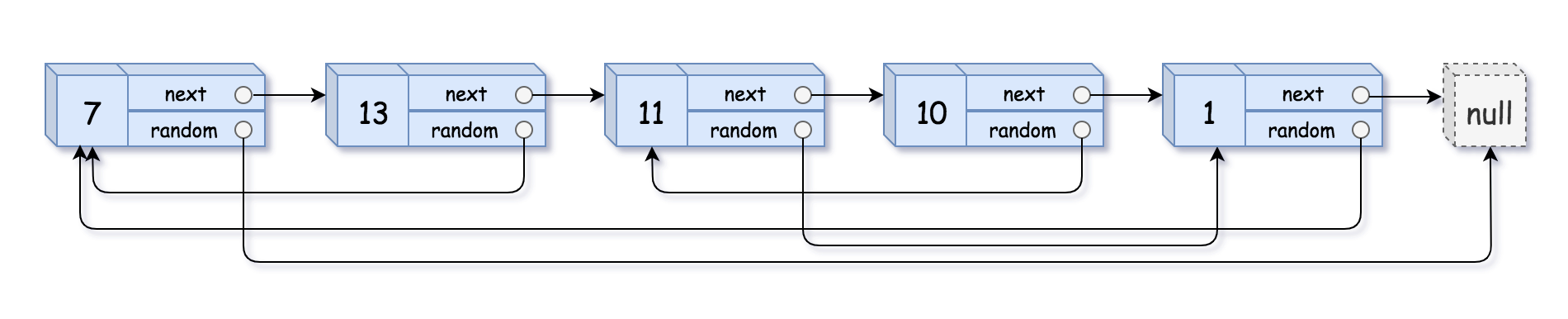
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]
struct Node* copyRandomList(struct Node* head) {
    if(head==NULL)
         return NULL;
    struct Node*p=head;
    struct Node*tail=NULL,*phead=NULL;
    while(p)
    {
        struct Node*newnode=(struct Node*)malloc(sizeof(struct Node));
        newnode->val=p->val;
        newnode->next=NULL;
        if(tail==NULL)
        {
            phead=newnode;
            tail=newnode;
        }
        else
        {
            tail->next=newnode;
            tail=tail->next;
        }
        p=p->next;
    }
    p=head;
    struct Node*cur=phead;

    struct Node *prev=phead;
    while(prev)
    {
        if(cur)
        {
            cur=cur->next;
        }
        prev->next=p->next;
        p->next=prev;
        p=p->next->next;
        prev=cur;
    }
    prev=head;
    cur=head->next;
    while(prev)
    {
        if(prev->random!=NULL)
            cur->random=prev->random->next;
        else
            cur->random=NULL;
        prev=cur->next;
        if(prev)
            cur=prev->next;
    }
    tail=phead;
    while(tail)
    {
        if(tail->next)
            tail->next=tail->next->next;
        else
            tail->next=NULL;
        tail=tail->next;
    }
    return phead;

}

我们需要将这个链表进行复制， 对于链表的数据和next指针我们很容易进行复制，但是这个随机指针我们很难，我们第一个想到的是数据进行比较但是由于链表的数据可以重复，我们就不能找到正确的数据，我们可以找到一个很妙的方法，我们先对数据进行数据和指针next的复制，

 我们将复制的链表的数据插入到原来的链表中，

 这样做是为了对数据进行定位，然后对随机指针进行复制，然后拆下链表重新形成新的链表。

3.总结

        今天的内容就结束了，非常欢迎大家来三连，也同时希望大家可以在这篇博客中学到很多东西。


http://www.kler.cn/a/135833.html

相关文章：

  • 掌握 Ansys ACP 中的参考方向：简化复杂的复合材料设计
  • sqoop的参数有哪些？
  • java 对ElasticSearch数据库操作封装工具类（对你是否适用嘞）
  • Gin-vue-admin（1）：环境配置和安装
  • MySQL数据库——复制表数据与结构
  • YoloV8改进策略：Head改进|DynamicHead，利用注意力机制统一目标检测头部|即插即用
  • HTTPS流量抓包分析中出现无法加载key
  • vscode Prettier配置
  • 苹果（Apple）公司的新产品开发流程（一）
  • 计蒜客T1654 数列分段（C语言实现）
  • 结合scss实现黑白主题切换
  • 趣学python编程 (五、常用IDE环境推荐)
  • 10 Redis的持久化
  • c++ 获取当前时间（精确至秒、毫秒和微妙）
  • 【代码随想录】算法训练计划27
  • springboot引入redisson分布式锁及原理
  • 深度学习之基于YoloV5-Pose的人体姿态检测可视化系统
  • 产品经理进阶：外包原因及类型（一）
  • Java获取Jar、War包路径，并生成可编辑修改的本地配置文件
  • 05-networkX-结构洞计算
  • Halcon Solution Guide I basics(2): Image Acquisition（图像加载）
  • 2024年csdn最新最全的Postman接口测试： postman定义公共函数
  • 锐捷OSPF认证
  • Postman启动问题：Could not open Postman
  • BLE协议栈入门学习
  • DSP2335的按键输入key工程笔记