【左程云算法全讲11】贪心算法 并查集
系列综述:
💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。
🥰来源:材料主要源于左程云算法课程进行的,每个知识点的修正和深入主要参考各平台大佬的文章,其中也可能含有少量的个人实验自证。
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
🌈【C++】秋招&实习面经汇总篇
文章目录
- 贪心算法
- 并查集
- 参考博客
😊点此到文末惊喜↩︎
贪心算法
- 需要整理堆的使用,重写cmp
auto cmp = [&](const int& a, const int &b) {
return cnt[a] < cnt[b];//此处cnt可由上文完成定义(最大堆--跟sort正好相反)
};
priority_queue<int, vector<int>, decltype(cmp)>pq{cmp};
- 分解过程
- 分解业务
- 根据业务逻辑找到不同的贪心策略
- 可以举出反例的贪心策略直接跳过,不能举出反例的要证明其有效性
- 贪心算法的解题套路
- 实现一个不依靠贪心策略的解法X,可以用最暴力的尝试
- 脑补出贪心策略A、贪心策略B、贪心策略C…
- 用解法X和对数器,用实验的方式得知哪个贪心策略正确
- 不要去纠结贪心策略的证明
- 贪心策略:通常使用堆和排序
- 示例:排序式贪心
- 题目:
- 一些项目要占用一一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。
- 给你每- -个项目开始的时间和结束的时间
- 你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。
- 返回最多的宣讲场次。
- 贪心思路:每次优先安排结束时间最早的,并且将无法安排的进行删除
- 题目:
- 示例:堆式贪心1
- 题目:
- 一块金条切成两部分,需要花费和原长度一样的铜板数量
- 比如长度为20的金条,不管怎么切,都要花费20个铜板。
- 一群人各自分到自己想要的金条部分(和为总长度),怎么分最省铜板?
- 思路1:每次尽可能的切下最大的部分
- 思路2:使用哈夫曼树,每次弹出最小的两个数合并后在压入
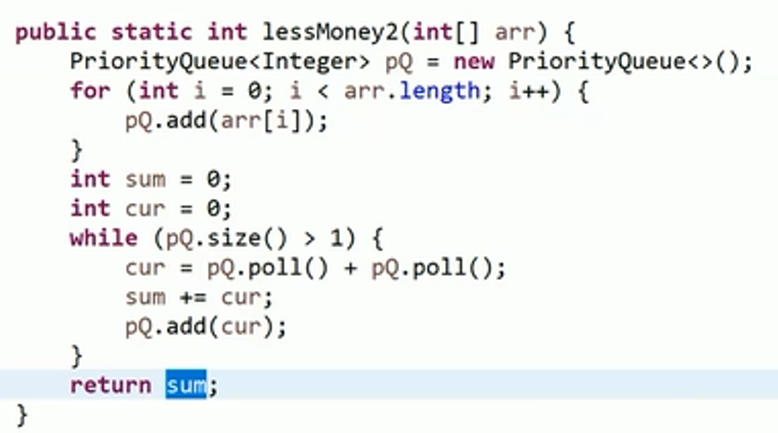
- 题目:
- 示例:堆式贪心2
- 题目:
- 输入:正数数组costs、正数数组profits、 正数K、正数M。costs[]表示i号项目的花费,profits[]表示i号项目在扣除花费之后还能挣到的钱(利润)
- K表示你只能串行的最多做k个项目,M表示你初始的资金
- 说明:每做完一个项目,马上获得的收益,可以支持你去做下一个项目。不能并行的做项目。
- 输出:你最后获得的最大钱数。
- 思路1:建立两个堆,一个以costs作为key的小根堆,一个是以profits作为key的大根堆。
struct Program { int p; int c Program(int profit, int cost) : p(profit), c(cost){} } int FindMaxProfits(vector<int> profits, vector<int> costs, int times, int surplus) { // 比较最小花费 auto cmp_min_cost = [](const Program &a, const Program &b)->bool{ return a.c < b.c; }; // 比较最大利润 auto cmp_max_profit = [](const Program &a, const Program &b)->bool{ return a.p > b.p; }; // 关于花费的小根堆 priority_queue<Program , vector<Program>, decltype(cmp_min_cost)> min_cost_pq; // 关于利润的大根堆 priority_queue<Program , vector<Program>, decltype(cmp_max_profit)> max_profit_pq; // 将所有花费压入优先队列中 for (int i = 0; i < profits.size(); ++i) { Program pg = {profits[i], costs[i]}; min_cost_pq.push(pg); } // 每次循环取出所有可支持的项目,并压入最大利润队列 for (int i = 0; i < times; ++i) { while (!min_cost_pq.empty() && min_cost_pq.top().c <= surplus){ Program pg = min_cost_pq.top(); min_cost_pq.pop(); max_profit_pq.push(pg); } // 如果最大利润队列为空,说明没有符合的项目可以继续进行 if (max_profit_pq.empty()) { return surplus; } // 获取最大利润 surplus += max_profit_pq.top().p; max_profit_pq.pop(); } } - 题目:
并查集
- 基本操作
- 并:合并两个子集为一个新的集合
- 查:通过查找一个结点的根节点,从而查找元素所属子集
- 作用:快速确定集合中的两两元素是否属于S的同一子集
- 基本并查集
- 问题:每一次Find操作的时间复杂度为O(H),H为树的高度,由于树的不断合并可能会使树严重不平衡,最坏情况每个节点都只有一个子节点,如下图3(第一个点为根节点)

#include <vector> class DisjSet { private: vector<int> parent; public: DisjSet(int max_size) : parent(vector<int>(max_size)) { // 各自为营:初始化每一个元素的根节点都为自身 for(int i = 0; i < max_size; i++) parent[i] = i; } // 查找:没找到就一直递归查看父亲结点 int find(int x) { return (parent[i] == x ? x : find(parent[i]); } // 合并:将 x1 所在的集合的根节点的父节点设置为 x2 所在集合的根节点 void to_union(int x1, int x2) { parent[find(x1)] = find(x2); } // 判断两个元素是否属于同一个集合 bool is_same(int e1, int e2) { return find(e1) == find(e2); } }; - 问题:每一次Find操作的时间复杂度为O(H),H为树的高度,由于树的不断合并可能会使树严重不平衡,最坏情况每个节点都只有一个子节点,如下图3(第一个点为根节点)
- 优化并查集
- 路径压缩:查询过程中,将沿途每个结点的父结点都设置为根结点,下次就可以减少查询路径长度
- 按秩合并:“按秩合并”。实际上就是在合并两棵树时,将高度较小的树合并到高度较大的树上。这里我们使用“秩”(rank)代替高度,秩表示高度的上界,通常情况我们令只有一个节点的树的秩为0,严格来说,rank + 1才是高度的上界;两棵秩分别为r1、r2的树合并,如果秩不相等,我们将秩小的树合并到秩大的树上,这样就能保证新树秩不大于原来的任意一棵树。如果r1与r2相等,两棵树任意合并,并令新树的秩为r1 + 1。
#include <vector> class DisjSet { private: std::vector<int> parent; std::vector<int> rank; // 秩 public: DisjSet(int max_size) : parent(std::vector<int>(max_size)), rank(std::vector<int>(max_size, 0)) { for (int i = 0; i < max_size; ++i) parent[i] = i; } int find(int x) { return x == parent[x] ? x : (parent[x] = find(parent[x])); } void to_union(int x1, int x2) { int f1 = find(x1); int f2 = find(x2); if (rank[f1] > rank[f2]) parent[f2] = f1; else { parent[f1] = f2; if (rank[f1] == rank[f2]) ++rank[f2]; } } bool is_same(int e1, int e2) { return find(e1) == find(e2); } }; - 并查集示例
- 题目
- 如果两个user,a字段一样,或者b字段一样、或者c字段一样,就认为是同一个人
- 请合并user,并返回合并后的人数
- 题目
struct User {
string a;
string b;
string c;
User(string a1, string b1, string c1) : a(a1), b(b1), c(c1){}
};
🚩点此跳转到首行↩︎
参考博客
- 知乎并查集
- 待定引用
- 待定引用
- 待定引用
