第1关：图的邻接表存储及求邻接点操作

• 任务要求
• 参考答案
• 评论2

• 任务描述
• 相关知识
• 编程要求
• 测试说明

任务描述

本关任务：要求从文件输入顶点和边数据，包括顶点信息、边、权值等，编写程序实现以下功能。 1）构造图G的邻接表和顶点集，即图的存储结构为邻接表。 2）输出图G的各顶点和邻接表。 3）输出图G中某个顶点的所有邻接顶点。

相关知识

对于图来说，邻接矩阵是不错的一种图存储结构，但是对于边数相对顶点较少的图，这种结构对存储空间浪费极大。

因此考虑另外一种存储结构方式：邻接表，即数组与链表相结合的存储结构。

在图的邻接表结构中，用一个连续存储区域来存储图中各顶点的数据，并对图中每个顶点vi建立一个单链表(称为vi的邻接表)，把顶点vi的所有相邻顶点(即后继结点)的序号链接起来。

第i个单链表中的每一个结点(也称为表结点)均含有三个域：邻接点域、链域和数据域，邻接点域用来存放与顶点vi相邻接的一个顶点的序号，链域用来指向下一个表结点，数据域info存储边的信息（如果边上没有权值，可以省略该info数据域）

另外每个顶点vi设置了表头结点，除了存储本身数据的数据域data外，还设置了一个链域firstarc，作为邻接表的表头指针，指向第一个表结点。n个顶点用一个一维数组表示。如图所示。

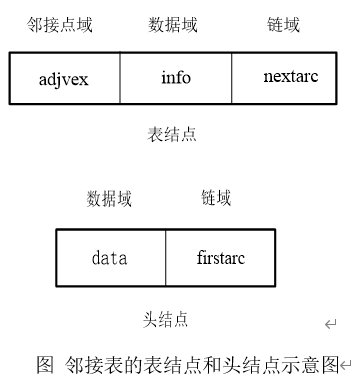
表结点的类型定义如下：

1. typedef struct
2. {
3. int adjvex; // 该弧所指向的顶点的位置
4. int info; // 网的权值
5. ArcNode *nextarc; // 指向下一条弧的指针
6. }ArcNode;

头结点的类型定义如下：

1. typedef struct
2. {
3. VertexType data; // 顶点信息
4. ArcNode *firstarc; // 第一个表结点的地址,指向第一条依附该顶点的弧的指针
5. }VNode,AdjList[MAX_VERTEX_NUM];

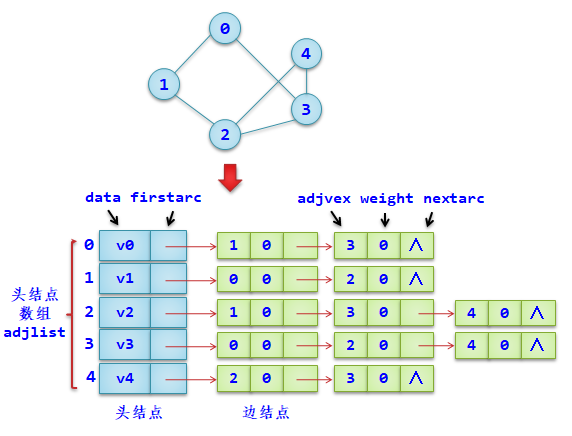
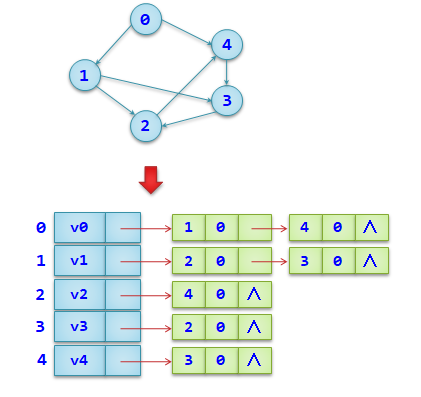
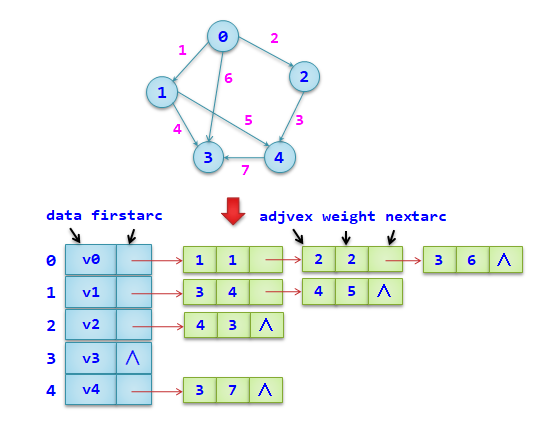
图的邻接表存储表示，类型定义如下：

1. typedef struct
2. {
3. AdjList vertices;
4. int vexnum,arcnum; // 图的当前顶点数和弧数
5. GraphKind kind; // 图的种类标志
6. }ALGraph;

邻接表具有如下性质：

1. 图的邻接表表示不是唯一的，它与表结点的链入次序有关，取决于建立邻接表的算法以及边的输入次序；
2. 无向图的邻接表中第i个边表的结点个数即为第i个顶点的度；
3. 有向图的邻接表中第i个出边表的结点个数即为第i个顶点的出度，有向图的逆邻接表中第i个入边表的结点个数即为第i个顶点的入度；
4. 无向图的边数等于邻接表中边表结点数的一半，有向图的弧数等于邻接表的出边表结点的数目，也等于逆邻接表的入边表结点的数目。

编程要求

根据提示，在右侧编辑器补充代码，要求从文件中输入顶点和边数据，包括顶点信息、边、权值等，编写函数实现图的基本运算：

• void CreateGraphF(ALGraph &G); // 采用邻接表存储结构，由文件构造没有相关信息图或网G

• void Display(ALGraph G); // 输出图的邻接表G

• int LocateVex(ALGraph G,VertexType u); //若G中存在顶点u，则返回该顶点在图中位置；否则返回-1

• int FirstAdjVex(ALGraph G,VertexType v); // 返回v的第一个邻接顶点的序号；否则返回-1

• int NextAdjVex(ALGraph G,VertexType v,VertexType w);//v是图G中某个顶点，w是v的邻接顶点，返回v的(相对于w的)下一个邻接顶点的序号

测试说明

平台会对你编写的代码进行测试：

测试输入： 3 lt.txt 徐州

输入说明： 第一行输入3，表示输入图的类型为无向网。 第二行输入文件名，该文件里保存了图的数据信息，内容如下：

第1行为图的顶点的个数n； 第2行为图的边的条数m； 第3行至第n+2行是n个顶点的数据； 第n+3行至第n+m+2行是m条边的数据； 第三行为一个顶点徐州的数据

预期输出： 无向网 8个顶点： 北京 天津 郑州 徐州 武汉 上海 株洲 南昌 9条弧(边): 北京→郑州 :695 北京→天津 :137 天津→徐州 :674 天津→北京 :137 郑州→武汉 :534 郑州→徐州 :349 郑州→北京 :695 徐州→上海 :651 徐州→郑州 :349 徐州→天津 :674 武汉→株洲 :409 武汉→郑州 :534 上海→徐州 :651 上海→南昌 :825 株洲→南昌 :367 株洲→武汉 :409 南昌→上海 :825 南昌→株洲 :367 上海 郑州 天津

#include<stdio.h> 
#include<stdlib.h> 
#include<string.h>
#include<limits.h> 
typedef char VertexType[20]; // 顶点类型为字符串 
#define MAX_VERTEX_NUM  20
typedef enum{DG,DN,UDG,UDN}GraphKind; // {有向图,有向网,无向图,无向网} 
typedef struct 
{
    int adjvex; // 该弧所指向的顶点的位置 
    int info; // 网的权值指针 
}ElemType;
typedef struct ArcNode 
{
    ElemType data;          // 除指针以外的部分都属于ElemType 
    struct ArcNode *nextarc;   // 指向下一条弧的指针 
}ArcNode;                // 表结点 
typedef struct
{
    VertexType data;         // 顶点信息 
    ArcNode *firstarc;       // 第一个表结点的地址,指向第一条依附该顶点的弧的指针 
}VNode,AdjList[MAX_VERTEX_NUM];  // 头结点 
typedef struct
{
    AdjList vertices;
    int vexnum,arcnum;       // 图的当前顶点数和弧数 
    GraphKind kind;          // 图的种类标志 
}ALGraph;

#define LNode ArcNode         // 定义单链表的结点类型是图的表结点的类型 
#define next nextarc         // 定义单链表结点的指针域是表结点指向下一条弧的指针域 
typedef ArcNode *LinkList;     // 定义指向单链表结点的指针是指向图的表结点的指针 
int LocateElem(LinkList L,ElemType e,int (*equal)(ElemType,ElemType));
LinkList Point(LinkList L,ElemType e,int(*equal)(ElemType,ElemType),LinkList &p);
int ListInsert(LinkList &L,int i,ElemType e);// 在不带头结点的单链线性表L中第i个位置之前插入元素e 

int equal(ElemType a,ElemType b);
void visit(VertexType i);
void CreateGraphF(ALGraph &G);         // 采用邻接表存储结构，由文件构造没有相关信息图或网G
void Display(ALGraph G);             // 输出图的邻接表G 
int LocateVex(ALGraph G,VertexType u);    //若G中存在顶点u，则返回该顶点在图中位置；否则返回-1
int FirstAdjVex(ALGraph G,VertexType v);  // 返回v的第一个邻接顶点的序号；否则返回-1 
int NextAdjVex(ALGraph G,VertexType v,VertexType w);//v是图G中某个顶点，w是v的邻接顶点，返回v的(相对于w的)下一个邻接顶点的序号

int main()
{
    ALGraph g;
    VertexType v1,v2;
    int k;
    CreateGraphF(g);       // 利用数据文件创建图
    Display(g);           // 输出图  
    //printf("请输入顶点的值: ");
    scanf("%s",v1);
    //printf("输出图G中顶点%s的所有邻接顶点: ",v1);
    k=FirstAdjVex(g,v1);
    while(k!=-1)
    {  
        strcpy(v2,g.vertices[k].data);
        visit(v2);
        k=NextAdjVex(g,v1,v2);
    }
    printf("\n");
    return 0;
}
int equal(ElemType a,ElemType b)
{   
    if(a.adjvex==b.adjvex)
        return 1;
    else
        return 0;
}
void visit(VertexType i)
{
    printf("%s ",i);
}

int LocateElem(LinkList L,ElemType e,int (*equal)(ElemType,ElemType))
{   // 初始条件: 不带头结点的单链表L已存在，equal()是数据元素判定函数(满足为1，否则为0) 
    // 操作结果: 返回L中第1个与e满足关系equal()的数据元素的位序。 
    //           若这样的数据元素不存在，则返回值为0 
    int i=0;
    LinkList p=L;  // L是不带头结点的单链表
    while(p)
    {
        i++;
        if(equal(p->data,e)) // 找到这样的数据元素 
            return i;
        p=p->next;
    }
    return 0;
}
LinkList Point(LinkList L,ElemType e,int(*equal)(ElemType,ElemType),LinkList &p)
{  //查找表L中满足条件的结点。如找到，返回指向该结点的指针，p指向该结点的前驱(若该结点是首元结点，则p=NULL)。
   //如表L中无满足条件的结点，则返回NULL，p无定义。函数equal()的两形参的关键字相等，返回OK；否则返回ERROR
    int i,j;
    i=LocateElem(L,e,equal);
    if(i)                  // 找到 
    {
        if(i==1)          // 是首元结点 
        {
            p=NULL;
            return L;
        }
        p=L;
        for(j=2;j<i;j++)
            p=p->next;
        return p->next;
    }
    return NULL;           // 没找到 
}
int  ListInsert(LinkList &L,int i,ElemType e)
{   // 在不带头结点的单链线性表L中第i个位置之前插入元素e 
    int j=1;
    LinkList p=L,s;
    if(i<1) // i值不合法 
        return 0;
    s=(LinkList)malloc(sizeof(struct LNode)); // 生成新结点 
    s->data=e;                         // 给s的data域赋值 
    if(i==1)                           // 插在表头 
    {
        s->next=L;
        L=s;                           // 改变L 
    }
    else
    { // 插在表的其余处 
        while(p&&j<i-1)                // 寻找第i-1个结点 
        {
            p=p->next;
            j++;
        }
        if(!p)                         // i大于表长+1 
            return 0;
        s->next=p->next;
        p->next=s;
    }
    return 1;    
}

void CreateGraphF(ALGraph &G)
{   // 采用邻接表 存储结构，由文件构造没有相关信息图或网G(用一个函数构造4种图) 
    /********** Begin **********/
    int i,j,k,w;            
	VertexType va,vb;      
	ElemType e;
	char filename[13];
	FILE *graphlist;
	scanf("%d",&G.kind);
	scanf("%s",filename);   
	graphlist=fopen(filename,"r");  
	fscanf(graphlist,"%d",&G.vexnum);
	fscanf(graphlist,"%d",&G.arcnum);
	for(i=0;i<G.vexnum;++i)        
	{
		fscanf(graphlist,"%s",G.vertices[i].data);
		G.vertices[i].firstarc=NULL;  
	}
	for(k=0;k<G.arcnum;++k)           
	{
		if(G.kind%2)                 
			fscanf(graphlist,"%s%s%d",va,vb,&w);
		else                         
			fscanf(graphlist,"%s%s",va,vb);
		i=LocateVex(G,va);          
		j=LocateVex(G,vb);          
		e.info=0;                   
		e.adjvex=j;                  
		if(G.kind%2)               
		{
			e.info = w;
		}
		ListInsert(G.vertices[i].firstarc,1,e); 
		if(G.kind>=2)  
		{
			e.adjvex=i;                  
			ListInsert(G.vertices[j].firstarc,1,e);  
		}
	}
	fclose(graphlist);           
    /********** End **********/
} 
void Display(ALGraph G)
{   // 输出图的邻接表G 
    /********** Begin **********/
    int i;
	LinkList p;
	switch(G.kind)
	{
      case DG: printf("有向图\n");break;
      case DN: printf("有向网\n");break;
      case UDG:printf("无向图\n");break;
      case UDN:printf("无向网\n");
	}
	printf("%d个顶点：\n",G.vexnum);
	for(i=0;i<G.vexnum;++i)
		printf("%s ",G.vertices[i].data);
	printf("\n%d条弧(边):\n",G.arcnum);
	for(i=0;i<G.vexnum;i++)
	{
		p=G.vertices[i].firstarc;
		while(p)
		{
			printf("%s→%s ",G.vertices[i].data,G.vertices[p->data.adjvex].data);
			if(G.kind%2)            
				printf(":%d\t",p->data.info );			
			p=p->nextarc;
		}
		printf("\n");
	}
    /********** End **********/
} 
int LocateVex(ALGraph G,VertexType u)
{   // 初始条件：图G存在，u和G中顶点有相同特征 
    // 操作结果：若G中存在顶点u，则返回该顶点在图中位置；否则返回-1 
    /********** Begin **********/
    int i;
    for(i=0;i<G.vexnum;++i)
        if(strcmp(u,G.vertices[i].data)==0) return i;
    return -1;
    /********** End **********/
}
int FirstAdjVex(ALGraph G,VertexType v)
{   // 初始条件：图G存在，v是G中某个顶点 
    // 操作结果：返回v的第一个邻接顶点的序号。若顶点在G中没有邻接顶点，则返回-1 
    /********** Begin **********/
    LinkList p;
	int v1;
	v1=LocateVex(G,v); 
	p=G.vertices[v1].firstarc;
	if(p)
		return p->data.adjvex;
	else
		return -1;
    /********** End **********/
}
int NextAdjVex(ALGraph G,VertexType v,VertexType w)
{   // 初始条件：图G存在，v是G中某个顶点，w是v的邻接顶点 
    // 操作结果：返回v的(相对于w的)下一个邻接顶点的序号。若w是v的最后一个邻接点，则返回-1 
    /********** Begin **********/
    LinkList p,p1; 
	ElemType e;
	int v1;
	v1=LocateVex(G,v);        
	e.adjvex=LocateVex(G,w); 
	p=Point(G.vertices[v1].firstarc,e,equal,p1);  
	if(!p||!p->next)          
		return -1;
	else                       
		return p->next->data.adjvex;
    /********** End **********/
}

输出说明： 第一行输出图的类型。 第二行起输出图的顶点和边的数据信息。 最后一行为徐州的邻接点。