考研数二第五讲 无穷小阶数问题的求解
无穷小阶数问题的求解
在考研复习中,关于无穷小阶数的问题是比较多的,从最基本的确定无穷小阶数问题,到无穷小之间的阶数 比较问题,都是属于比较常见的类型。此外,还有一些其他的切入点的题目,值得多多注意。

题目没有说明具体是多少阶,而是让我们自己去尽可能确定无穷小的阶数,这种问法就相对来说比较有新意。最好的解法还是麦克劳林展开式:
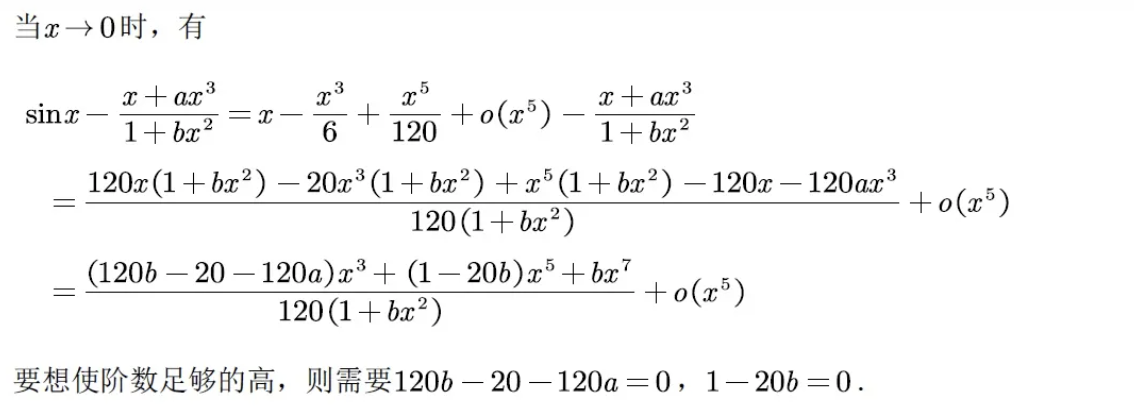
要想使阶数足够的高,就要尽可能使低阶项的系数为0,通过解方程求得结果。
关于无穷小阶数的问题,常规的做法一般都是借助麦克劳林展开式进行展开,确定第一个系数不为零的最低阶数,最终确定无穷小的阶数。除此以外,还有一种做法不常见,但也很值得学习,下题就是一个非常典型的例子。
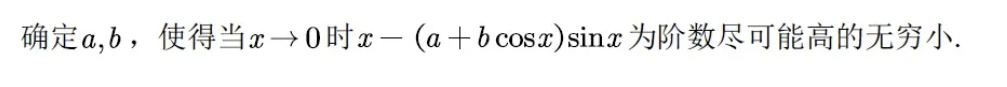

所以另y'(0)=y'''(0)=0
利用了一般函数的麦克劳林展开式,并令低阶导数尽可能等于0,确定未知参数,这样就达到题干中的无穷小阶数尽可能小的要求,也是值得借鉴的做法
一个常见函数的等价无穷小
有一个常见函数,它在考研里出现的几率极高,由它带出来的性质也比较多,今天会看到它的一个关于等价无穷小的性质,后续我们还会看到它在其他章节知识的出场。请看下题:
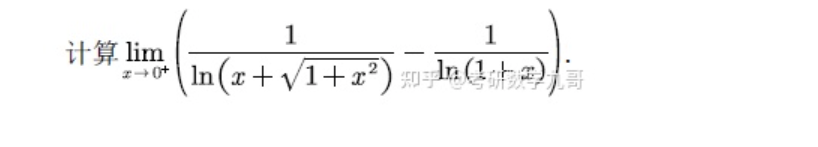
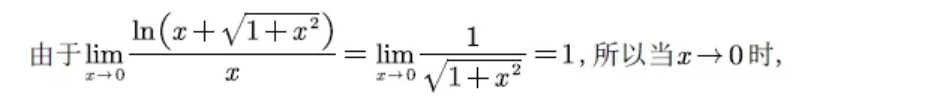
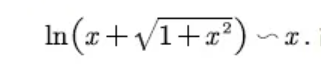
所以原题可得:
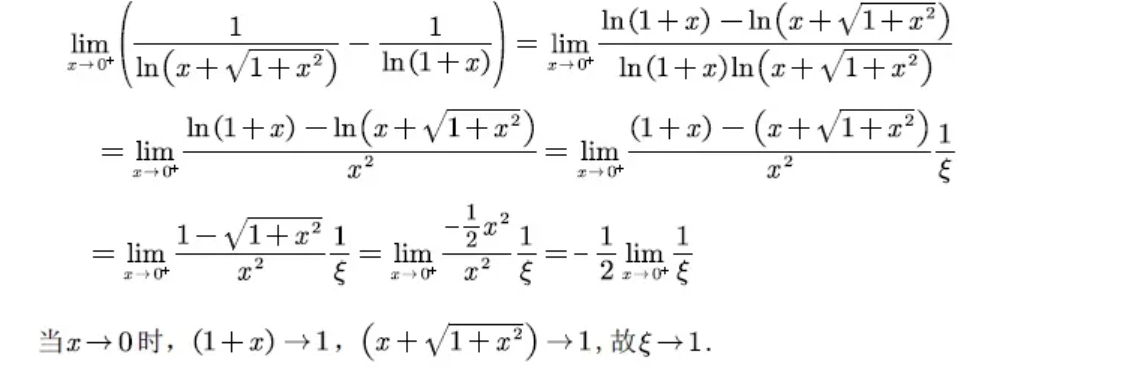
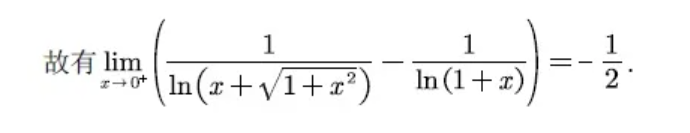
所说的这个等价无穷小,就是如下的这个: