多重背包的单调队列优化
邮专学子周末早起迎寒风细雨所作............. 周末也别想休息！！！
耐心看完，必定有收获哦🥰🐯
多重背包与其他背包相比的最大区别点就是，每个物品的数量是有限的。下面我们来看看多重背包的更新特性，可以从递推公式上琢磨琢磨.......
相关参数的解释
v代表体积，w代表价值，s代表物品数量，i代表放入背包的第i件物品，g数组存放没有放入i物品前各容量背包的原始价值，其它参数根据情况而定。
单调队列
元素值不递增的队列，谓之单调队列，还没弄懂概念的同学可以去搜索相关博客进行理解
背包更新的特性
测试代码
#include<iostream>
#include<cstdio>
using namespace std;
int dp[1005];
int main() {
int N, V;
cin >> N >> V;
for (int i = 1;i <= N;i++) {
//从背后开始遍历,避免物品重放
int v, w, s;
cin >> v >> w >> s;
for (int j = V;j >= v;j--) {
for (int k = 1;k <= s;k++) {
if (j >= k * v) {
dp[j] = max(dp[j], dp[j - k * v] + k * w);
printf("dp[%d] = %d dp[%d] = dp[%d] + %d*%d\n", j, dp[j], j, j - k * v, k, w);
}
else {
break;
}
}
}
}
cout << dp[V] << endl;
return 0;
}
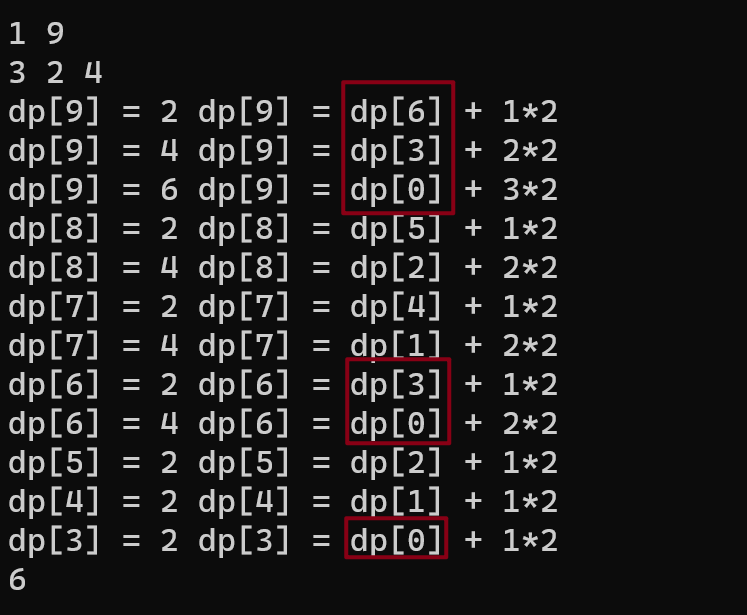
递推公式：dp[j] = max(dp[j], dp[j - k * v] + k * w)
很显然，背包dp[j]的最大值是由其自身得到，或者是从容量与其相差k*v的背包更新而来。姑且认定容量之间相差k*v的背包为一类，那么对于放入体积为v的物品，背包更新的种类就可以分为起始容量为0,1,2......v-1种，比如dp[0],dp[0+v],dp[0+2v]......dp[0+k*v]......
从此处开始，参数的含义与测试代码不同。
j表示同类背包的起始容量,k表示待更新最大值的背包容量,t表示物品相差个数。
很显然，背包只能在同类间更新，且被更新背包的容量较大,倘若能够一次性选取到dp[k-t*v]+t*w最大的背包maxBag(定义名词)，该背包的容量为k-t*v，那么背包dp[k]的最大值只需要更新一次，时间复杂度为O(1)。为了简化问题的讨论，我们姑且认为dp[k]就是从同类背包dp[k-t*v]的基础上更新而来，下面讨论如何遍历特点与选取价值最大的容量背包maxBag。
遍历特点
由于背包在同类间更新，而且较大容量背包的最大价值是由较小背包的最大价值推导而来，因此遍历背包的顺序是从小容量到大容量。然而，这种更新方式会使物品重复放入，因而需要用一个辅助数组g来存放在没有放入第i件物品之前，各个容量背包的最大价值。那么递推公式应该为:
dp[k] = max(g[k],g[k-t*v]+t*v)
如何选取maxBag
(j代表同类背包的起始容量，牢记参数含义)
给出存放规则如下：倘如g[k2] - (k2 - j)/v*w >=g[k1] - (k1 - j)/v*w ，那么
由于i物品的数量s有限，故dp[k]背包所借助的maxBag，其容量vv,必须满足如下关系式: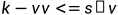 
；因此，由于maxBag的使用受到物品个数影响，故当maxBag1不能再被使用时，需要借助maxBag2，也就是说，我们需要借助一个队列来存放此类背包{maxBag1,maxBag2......maxBag(n)},倘若待更新背包的容量k满足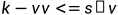：，那么maxBag1更新最大容量，否则maxBag1退出队列，借助maxBag2更新dp[k]的最大价值。
因而，我们需要借助 int q[maxn]来存放maxBag,队头的下标为hh,队尾的下标为tt,q[x]代表maxBag的背包容量，下面给出maxBag的入队规则，假如 g[k1] - (k1-j)/v*w >= g[k2] - (k2 - j)/v*w,那么容量为k1的背包必定排在容量为k2的背包前面，这是因为当我们分别讨论dp[k]借助g[k1],g[k2]更新最大价值时(依旧先前规定，不讨论dp[k]借助自身更新最大值)：
dp[k] = g[k1] + (k-k1)/v*w >= dp[k] = g[k2] + (k - k2)/v*w，该不等式很容易证明。
总而言之，倘若q[hh]代表队头背包的容量，因而 当(k-q[hh])>s*v时，hh++,当dp[k]结束更新后需要考虑将其加入队列,dp[k]的更新公式如下:
dp[k] = max(g[k], g[q[hh]] + (k - q[hh]) / v * w)
代码实现
语言:C++ 环境:VS2022
（可以用于通过AcWing困难级别的多重背包问题）
#include<iostream>
#include<cstdio>
using namespace std;
const int maxv = 20005;
const int maxn = 1005;
int dp[maxv];
int g[maxv];
int main() {
int N, V;
cin >> N >> V;
//确保容量的最大值不超过maxv
if (V >= maxv) {
return 0;
}
//依次放入N件物品
for (int i = 1;i <= N;i++) {
int v, s, w;
cin >> v >> w >> s;
//将v分类,g表示在放入i物品之前的各容量背包的价值状态
memcpy(g, dp, sizeof dp);
for (int j = 0;j < v;j++) {
//讨论容量为k的背包的更新,hh表示队头，tt表示队尾
//q[hh]存放最大净值背包的容量
int hh = 0, tt = -1;
int q[maxv] = { 0 };
for (int k = j;k <= V;k += v) {
//如果队列的长度大于物品的个数，那么需要更新队头
if (hh <= tt && (k - q[hh]) > s * v)
hh++;
//更新最大容量
if (hh <= tt)
dp[k] = max(g[k], g[q[hh]] + (k - q[hh]) / v * w);
//将dp[k]
while (hh <= tt && g[q[tt]] - (q[tt] - j) / v * w <= g[k] - (k - j) / v * w)
tt--;
q[++tt] = k;
}
}
}
cout << dp[V] << endl;
return 0;
}算法的时间复杂度
由于每当加入一个物品时，各个容量的背包只需要更新一次，因此倘若不包括队列的更新，则时间复杂度为O(NV),N代表物品个数，V代表背包最大容量。再讨论最内层的队列更新循环，由于队列最大长度不超过物品的个数s，故更新最好的情况为O(1),最坏情况为O(s),故总体时间复杂度的范围是:O(NV)~O(NVs),由于s是一个变量，而且相对于NV而言比较小，姑且认为时间复杂度为O(NV).相比如朴素算法的O(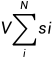
)已经提升一大截了。
结语
队列优化多重背包算法涉及将背包本身按照容量分类的思想（二进制优化是将物品个数分类），需要理解其分类思想，背包更新的特性以及如何利用单调队列更新最大价值.......
思路有点复杂，一遍看不懂不要灰心，多去看看别人的博客，多看看相关视频，多敲几遍代码自己体会，很快就会有头绪了（本人也是花了一整天时间才了解了一点点）。最后希望同学们若真的理解了，将自己的理解分享出去，这样会进一步加深对该算法的理解呢。
结束！！！