【算法】装备合成（二分）

链接：登录—专业IT笔试面试备考平台_牛客网
来源：牛客网

题目描述

牛牛有x件材料a和y件材料b，用2件材料a和3件材料b可以合成一件装备，用4件材料a和1件材料b也可以合成一件装备。牛牛想要最大化合成的装备的数量，于是牛牛找来了你帮忙。

输入描述:

输入包含t组数据
第一行一个整数t
接下来t行每行两个整数x,y

输出描述:

每组数据输出一行一个整数表示答案。

输入

5
4 8
7 6
8 10
100 4555
45465 24124

输出

2
2
3
50
13917

备注:

1<=t<=10000{1<=t<=10000}1<=t<=10000

1<=x,y<=1e9{1<=x,y<=1e9}1<=x,y<=1e9

思路

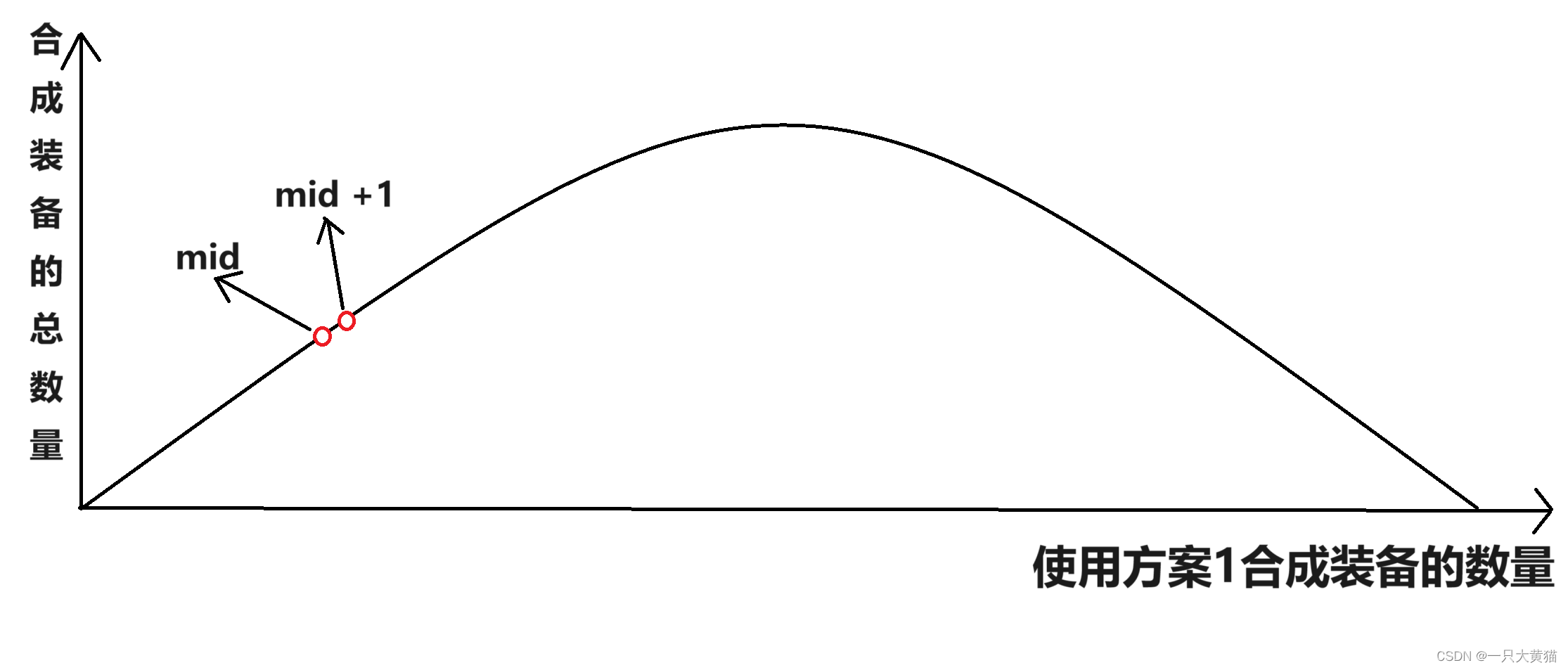
使用方案1合成装备的数量与合成装备的总数量关系如图所示。

设需要用方案一制造装备m件，消耗a材料（2*m）件，消耗材料b（3*m）件。

那么使用方案二制造装备数为min((x - 2 * m) / 4,(y - 3 * m) / 1)。

我们可以使用二分的方法来寻找m。

比较mid与mid + 1制造的装备总数，如果m = mid时制造的装备总数小于m = mid + 1时制造的装备总数，则mid在峰值的左侧，否则在峰值的右侧，找到峰值时，即为可以制造装备总数的最大值。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int x,y;

bool check(int mid)
{
    int xx1 = x - (2 * mid);
    int yy1 = y - (3 * mid);
    if(xx1 < 0) return true; 
    if(yy1 < 0) return true;
    int res1 = min(xx1 / 4, yy1 / 1);
    res1 += mid;
    
    mid ++;
    int xx2 = x - (2 * mid);
    int yy2 = y - (3 * mid);
    if(xx2 < 0) return true; 
    if(yy2 < 0) return true;
    int res2 = min(xx2 / 4, yy2 / 1);
    res2 += mid;
    
    if(res1 > res2) return true;
    else return false;
    
}

void solve()
{
    cin >> x >> y;
    int l = 0, r = 1e9;
    while(l < r)
    {
        int mid = (l + r) >> 1;
        if(check(mid)) r = mid;
        else l = mid + 1;
    }
    int xx1 = x - (2 * l);
    int yy1 = y - (3 * l);
    int res1 = min(xx1 / 4, yy1 / 1);
    cout << l + res1 << endl;
}

int32_t main()
{
    int T;
    cin >> T;
    while(T --)
        solve();
    return 0;
}