【机器学习】聚类(二):原型聚类:LVQ聚类(学习向量量化)
文章目录
- 一、实验介绍
- 1. 算法流程
- 2. 算法解释
- 3. 算法特点
- 4. 应用场景
- 5. 注意事项
- 二、实验环境
- 1. 配置虚拟环境
- 2. 库版本介绍
- 三、实验内容
- 0. 导入必要的库
- 1. LVQ类
- a. 构造函数
- b. 闵可夫斯基距离
- c. LVQ聚类过程
- e. 聚类结果可视化
- 2. 辅助函数
- 3. 主函数
- a. 命令行界面 (CLI)
- b. 数据加载
- c. 模型训练及可视化
- 4. 运行脚本的命令
- 5. 代码整合
学习向量量化(LVQ)是一种原型聚类算法,它在寻找原型向量以刻画数据集聚类结构的过程中利用了样本的类别标记。相较于一般聚类算法,LVQ通过监督信息辅助聚类,使得原型向量更好地代表各个聚类簇。
一、实验介绍
1. 算法流程

在学习过程中,LVQ算法通过样本的类别标记来引导原型向量的学习,使得原型向量更好地代表各个聚类簇。算法的性能高度依赖于初始化、学习率的设定以及停止条件的选择。
2. 算法解释
- 在初始化阶段,原型向量通过随机选取相应类别标记的样本进行初始化。
- 在学习过程中,算法通过计算距离和类别标记的一致性来引导原型向量的学习。相似类别的样本有助于更新原型向量,从而更好地代表该类别。
3. 算法特点
- LVQ算法结合了监督学习和聚类,通过使用类别标记进行引导,更好地适应样本的分布。
- 对于有监督信息的数据集,LVQ通常能够获得更具有判别性的聚类结果。
- 学习率η的选择对算法的性能有影响,需要根据具体情况进行调整。
4. 应用场景
- 适用于样本集带有类别标记的情况,尤其在需要获得判别性聚类结果的场景中。
- 在需要将样本分配到与其最相似的原型向量所代表的簇中的应用中表现良好。
5. 注意事项
- 初始原型向量的选择可能影响最终聚类结果,因此在具体应用中需要仔细选择初始原型向量。
- 学习率的选择需要谨慎,过大的学习率可能导致原型向量的不稳定更新,而过小的学习率可能使得算法收敛缓慢。
二、实验环境
1. 配置虚拟环境
conda create -n ML python==3.9
conda activate ML
conda install scikit-learn matplotlib seaborn pandas
2. 库版本介绍
| 软件包 | 本实验版本 |
|---|---|
| matplotlib | 3.5.2 |
| numpy | 1.21.5 |
| pandas | 1.4.4 |
| python | 3.9.13 |
| scikit-learn | 1.0.2 |
| seaborn | 0.11.2 |
三、实验内容
0. 导入必要的库
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import argparse
import random
1. LVQ类
__init__:初始化LVQ聚类的参数minkowski_distance函数:计算两个样本点之间的闵可夫斯基距离fit方法:执行LVQ聚类的迭代过程visualization函数:使用Seaborn和Matplotlib可视化聚类结果
a. 构造函数
class LVQ(object):
def __init__(self, features, labels, p=2, eta=0.1, max_iters=10, epsilon=1e-6, seed=0):
# 初始化LVQ类的属性
self.features = features # 样本特征
self.num_samples, self.num_features = self.features.shape
self.labels = labels # 样本标签
self.num_classes = len(np.unique(self.labels)) # 类别数
self.p = p # Minkowski距离的阶数
self.eta = eta # 学习率
self.max_iters = max_iters # 最大迭代次数
self.epsilon = epsilon # 停止条件,更新幅度小于epsilon时停止
self.seed = seed # 随机种子
self.proto = None # 原型向量
b. 闵可夫斯基距离
def minkowski_distance(self, x, y=0):
return np.linalg.norm(x - y, ord=self.p)
- 使用了NumPy的
linalg.norm函数,其中ord参数用于指定距离的阶数。
c. LVQ聚类过程
def fit(self):
random.seed(self.seed)
# 每类中随机选择一个原型向量
self.proto = np.array([random.choice(self.features[self.labels == c]) for c in range(self.num_classes)])
for i in range(self.max_iters):
index = random.randint(0, self.num_samples-1) # 随机选取一个样本
xj = self.features[index] # 样本特征
yj = self.labels[index] # 样本标签
dist = [self.minkowski_distance(d) for d in xj - self.proto] # 计算到各个原型向量的距离
min_idx = np.argmin(dist)
delta = self.eta * (xj - self.proto[min_idx])
if yj == min_idx:
# 更新原型向量
self.proto[min_idx] += delta
else:
self.proto[min_idx] -= delta
# 更新原型向量
if self.minkowski_distance(delta) < self.epsilon:
break
- 在初始化原型向量后,LVQ通过迭代过程不断调整原型向量,以适应样本的分布。
- 随机选择一个样本,计算该样本与所有原型向量的距离,并找到最近的原型向量。
- 根据样本标签和最近原型向量的类别标记更新原型向量。
e. 聚类结果可视化
def visualization(self):
current_palette = sns.color_palette()
sns.set_theme(context="talk")
clu_idx = np.zeros_like(self.labels, dtype=np.int64)
for i, x in enumerate(self.features):
dist = [self.minkowski_distance(d) for d in x - self.proto]
clu_idx[i] = np.argmin(dist)
for c in range(self.num_classes):
x = self.features[clu_idx == c]
sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8, color=current_palette[c])
sns.scatterplot(x=[self.proto[c][0]], y=[self.proto[c][1]], color=current_palette[c], marker='+', s=500)
plt.show()
2. 辅助函数
def order_type(v: str):
if v.lower() in ("-inf", "inf"):
return -np.inf if v.startswith("-") else np.inf
else:
try:
return float(v)
except ValueError:
raise argparse.ArgumentTypeError("Unsupported value encountered")
order_type函数:用于处理命令行参数中的-p(距离测量参数),将字符串转换为浮点数。
3. 主函数
a. 命令行界面 (CLI)
- 使用
argparse解析命令行参数
parser = argparse.ArgumentParser(description="LVQ Demo")
parser.add_argument("-m", "--max-iters", type=int, default=400, help="Maximum iterations")
parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")
parser.add_argument("--eta", type=float, default=0.1, help="Learning rate")
parser.add_argument("--eps", type=float, default=1e-6)
parser.add_argument("--seed", type=int, default=110, help="Random seed")
parser.add_argument("--dataset", type=str, default="./lvq.1.csv", help="Path to dataset")
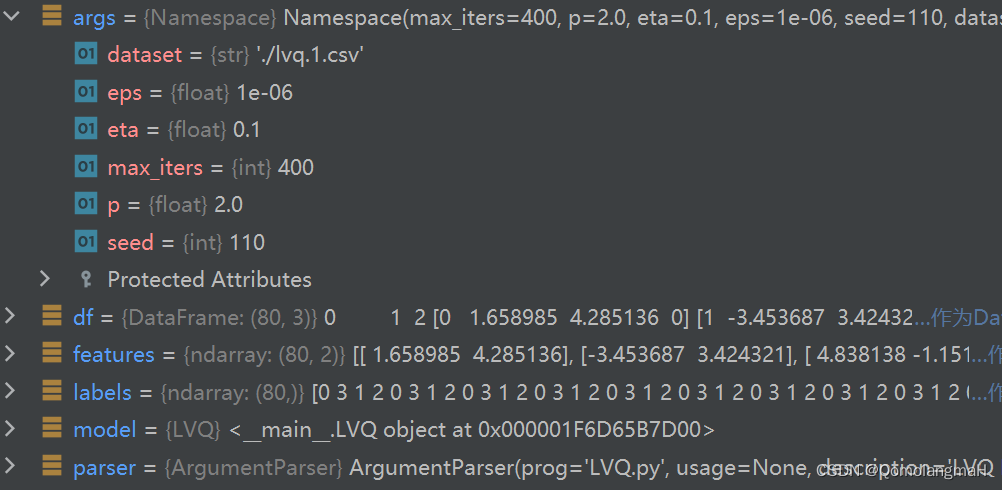
args = parser.parse_args()
b. 数据加载
- 从指定路径加载数据集。
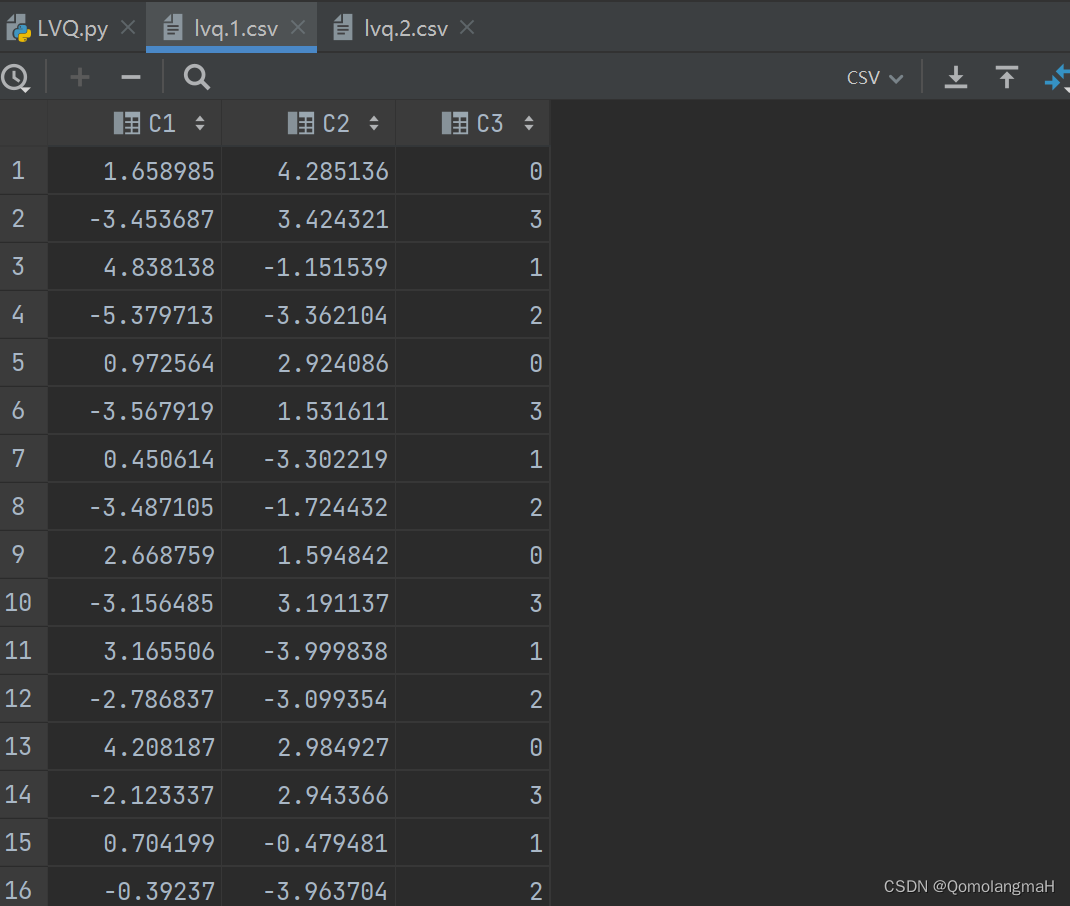
df = pd.read_csv(args.dataset, header=None)
features = df.iloc[:, [0, 1]].to_numpy()
labels = df.iloc[:, 2].to_numpy()
c. 模型训练及可视化
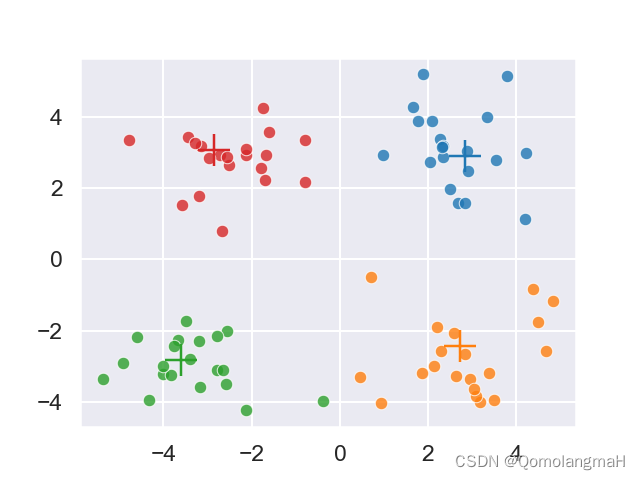
model = LVQ(features, labels, p=args.p, eta=args.eta, max_iters=args.max_iters, epsilon=args.eps, seed=args.seed)
model.fit()
model.visualization()
4. 运行脚本的命令
- 通过命令行传递参数来运行脚本,指定聚类数目、初始化模式、最大迭代次数等。
python LVQ.py -k 3 --mode random -m 100 -p 2 --seed 0 --dataset ./lvq.1.csv
5. 代码整合
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import argparse
import random
class LVQ(object):
def __init__(self, features, labels, p=2, eta=0.1, max_iters=10, epsilon=1e-6, seed=0):
self.features = features
self.num_samples, self.num_features = self.features.shape
self.labels = labels
self.num_classes = len(np.unique(self.labels))
self.p = p
self.eta = eta
self.max_iters = max_iters
self.epsilon = epsilon
self.seed = seed
self.proto = None
def minkowski_distance(self, x, y=0):
return np.linalg.norm(x - y, ord=self.p)
def fit(self):
random.seed(self.seed)
# 每类中随机选择一个原型向量
self.proto = np.array([random.choice(self.features[self.labels == c]) for c in range(self.num_classes)])
for i in range(self.max_iters):
index = random.randint(0, self.num_samples-1) # 随机选取一个样本
xj = self.features[index] # 样本特征
yj = self.labels[index] # 样本标签
dist = [self.minkowski_distance(d) for d in xj - self.proto] # 计算到各个原型向量的距离
min_idx = np.argmin(dist)
delta = self.eta * (xj - self.proto[min_idx])
if yj == min_idx:
# 更新原型向量
self.proto[min_idx] += delta
else:
self.proto[min_idx] -= delta
# 更新原型向量
if self.minkowski_distance(delta) < self.epsilon:
break
def visualization(self):
current_palette = sns.color_palette()
sns.set_theme(context="talk")
clu_idx = np.zeros_like(self.labels, dtype=np.int64)
for i, x in enumerate(self.features):
dist = [self.minkowski_distance(d) for d in x - self.proto]
clu_idx[i] = np.argmin(dist)
for c in range(self.num_classes):
x = self.features[clu_idx == c]
sns.scatterplot(x=x[:, 0], y=x[:, 1], alpha=0.8, color=current_palette[c])
sns.scatterplot(x=[self.proto[c][0]], y=[self.proto[c][1]], color=current_palette[c], marker='+', s=500)
plt.show()
def order_type(v: str):
if v.lower() in ("-inf", "inf"):
return -np.inf if v.startswith("-") else np.inf
else:
try:
return float(v)
except ValueError:
raise argparse.ArgumentTypeError("Unsupported value encountered")
if __name__ == '__main__':
parser = argparse.ArgumentParser(description="LVQ Demo")
parser.add_argument("-m", "--max-iters", type=int, default=400, help="Maximum iterations")
parser.add_argument("-p", type=order_type, default=2., help="Distance measurement")
parser.add_argument("--eta", type=float, default=0.1, help="Learning rate")
parser.add_argument("--eps", type=float, default=1e-6)
parser.add_argument("--seed", type=int, default=110, help="Random seed")
parser.add_argument("--dataset", type=str, default="./lvq.1.csv", help="Path to dataset")
args = parser.parse_args()
df = pd.read_csv(args.dataset, header=None)
features = df.iloc[:, [0, 1]].to_numpy()
labels = df.iloc[:, 2].to_numpy()
model = LVQ(features, labels, p=args.p, eta=args.eta, max_iters=args.max_iters, epsilon=args.eps, seed=args.seed)
model.fit()
model.visualization()
