事件抽取:Document-level Event Extraction via Parallel Prediction Networks
任务:给定一篇文章,从中提取出一个或多个结构化的事件
Y
=
{
y
i
}
i
=
1
k
Y=\{y_i\}_{i=1}^{k}
Y={yi}i=1k ,其中每个事件
t
t
t事件类型
y
i
t
y_{i}^{t}
yit表示是,包含一系列角色
(
r
i
1
,
r
i
2
,
.
.
.
,
r
i
n
)
(r_{i}^{1},r_{i}^{2},...,r_{i}^{n})
(ri1,ri2,...,rin),这些角色被论元
(
a
i
1
,
a
i
2
,
.
.
.
,
a
i
n
)
(a_{i}^{1},a_{i}^{2},...,a_{i}^{n})
(ai1,ai2,...,ain)填充。

2.1备选论元识别
给定有
N
S
N_S
NS个句子的文档
D
=
{
S
i
}
i
N
s
D=\{S_i\}_i^{N_s}
D={Si}iNs,首先进行编码得到上下文化的表示。
C
i
=
T
r
a
n
s
f
o
r
m
e
r
−
1
(
S
i
)
C_i=Transformer-1(S_i)
Ci=Transformer−1(Si) 给定文档的上下文感知的嵌入表示为
{
C
i
}
i
=
1
N
s
\{C_i\}_{i=1}^{N_s}
{Ci}i=1Ns。
句子级别的候选论元识别堪为序列标注任务(BIO),从给定句子中
S
i
S_i
Si得到候选论元
A
=
{
a
i
}
i
=
1
N
a
A=\{a_i\}_{i=1}^{N_a}
A={ai}i=1Na。
N
a
N_a
Na是识别出的候选论元的个数。
2.2 文档级别的编码器
第
i
i
i个句子中的论元span
[
c
i
,
j
,
.
.
.
,
c
i
,
k
]
[c_{i,j},...,c_{i,k}]
[ci,j,...,ci,k],执行最大池化,得到论元的局部嵌入
c
i
a
∈
R
d
c_{i}^{a}∈\mathbb{R}_{d}
cia∈Rd。句子的嵌入类似,第
i
i
i个句子
C
i
C_i
Ci,执行最大池化,得到句子嵌入
c
i
a
∈
R
d
c_{i}^{a}∈\mathbb{R}_{d}
cia∈Rd。其中
d
d
d是隐藏层的尺寸。
为每个句子添加sentence position嵌入表示句子顺序,如下图。送入transformer后通过多投资注意力机制,建模所有句子和候选论元的交互,得到文档感知的句子和论元表示。
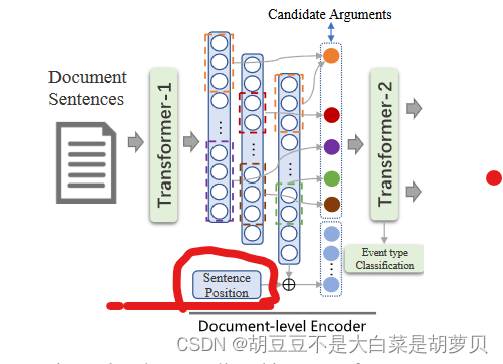
公式表示:
[
H
a
;
H
s
]
=
T
r
a
n
s
f
o
r
m
e
r
−
2
(
c
1
a
.
.
.
c
N
a
a
;
c
1
s
.
.
.
c
N
s
s
)
[H^a;H^s]=Transformer-2(c_{1}^{a}...c^{a}_{N_a};c_{1}^{s}...c_{N_s}^{s})
[Ha;Hs]=Transformer−2(c1a...cNaa;c1s...cNss)由于论元在一个文件中可能有很多提及,我们利用最大池化技术将具有相同字符级标记的多个参数嵌入合并为一个嵌入。
最终,合并后的候选论元
A
′
=
{
a
i
}
i
=
1
N
a
′
A'=\{a_i\}_{i=1}^{N_{a}'}
A′={ai}i=1Na′表示为
H
a
∈
R
N
a
′
×
d
H^a∈\mathbb{R}^{N_{a}'×d}
Ha∈RNa′×d,文档感知的句子表示
H
s
∈
R
N
s
×
d
H^s∈\mathbb{R}^{N_s×d}
Hs∈RNs×d。
在解码之前,我们通过对
H
s
H_s
Hs进行最大池化操作,堆叠一个线性分类器,对每个事件类型进行二元分类。
2.3 多粒度解码器
为了解决论元分散、多事件问题提出了多粒度解码器,包括事件解码器、角色解码器、事件to角色解码器三个部分。这三个粒度的解码器都是基于非自回归机制的,基于文档感知的H_a和H_s,平行生成所有可能的事件。
事件解码器
在解码前,解码器需要知道待生成事件的尺寸。文章使用了m个可学习的嵌入作为事件解码器的输入,表示为
Q
e
v
e
n
t
∈
R
m
×
d
Q_{event}∈\mathbb{R}^{m×d}
Qevent∈Rm×d。其中,m是超参数,表示了生成事件的数目,在实验中被设定为远大于文档中事件数目的平均值。
Event-Decoder是一个非自回归的解码器,用于平行提取所有事件。由N层相同的Transformer层堆叠而成。每一层包含两部分,多头自注意力机制建模事件间的交互,多头跨注意力机制将文档感知的表示
H
s
H_s
Hs整合到事件查询
Q
e
v
e
n
t
Q_{event}
Qevent中。
m
m
m个事件查询解码为
m
m
m 个输出嵌入:
H
e
v
e
n
t
=
E
v
e
n
t
−
D
e
c
o
d
e
r
(
Q
e
v
e
n
t
;
H
s
)
H_{event}=Event-Decoder(Q_{event};H^s)
Hevent=Event−Decoder(Qevent;Hs)其中
H
e
v
e
n
t
∈
R
m
×
d
H^{event}∈\mathbb{R}^{m×d}
Hevent∈Rm×d。
角色解码器
role decoder用于平行填充一个事件中的所有角色,建模角色间的交互。一个预测的事件类型
t
t
t 有
n
n
n 个语义角色类型
(
r
1
,
r
2
,
.
.
.
,
r
n
)
(r_1,r_2,...,r_n)
(r1,r2,...,rn),所以
Q
r
o
l
e
Q^{role}
Qrole 由
n
n
n 个可学习的嵌入组成。与事件解码器相同,自注意力机制建模角色之间的关系,跨注意力机制融合文档感知的候选论元
H
a
H^a
Ha表示的信息。
H
r
o
l
e
=
R
o
l
e
−
D
e
c
o
d
e
r
(
Q
r
o
l
e
;
H
a
)
H^{role}=Role-Decoder(Q^{role};H^a)
Hrole=Role−Decoder(Qrole;Ha)其中,
H
r
o
l
e
∈
R
n
×
d
H^{role}∈\mathbb{R}^{n×d}
Hrole∈Rn×d
事件to角色解码器
针对不同的事件查询(queries),为了生成多种形式的有相关论元的事件,设计了event-to-role的解码器。建模事件查询
H
e
v
e
n
t
H^{event}
Hevent和角色查询
H
r
o
l
e
H^{role}
Hrole间的交互。
H
e
2
r
=
E
v
e
n
t
2
R
o
l
e
−
D
e
c
o
d
e
r
(
H
r
o
l
e
;
H
e
v
e
n
t
)
H^{e2r}=Event2Role-Decoder(H^{role};H^{event})
He2r=Event2Role−Decoder(Hrole;Hevent)其中,
H
e
2
r
∈
R
m
×
n
×
d
H^{e2r}∈\mathbb{R}^{m×n×d}
He2r∈Rm×n×d。
2.4 事件预测
上一阶段得到了m个预测事件,每个事件包含n个角色嵌入。为了过滤掉虚假事件,通过FFN网络做二分类,判断每个事件预测是否为空。
p
e
v
e
n
t
=
s
o
f
t
m
a
x
(
H
e
v
e
n
t
W
e
)
p^{event}=softmax(H^{event}W_e)
pevent=softmax(HeventWe)
其中,
W
e
∈
R
d
×
2
W_e∈\mathbb{R}^{d×2}
We∈Rd×2是可学习的参数。
对于每个有预定角色的预测事件,通过用
(
N
a
′
+
1
)
(N_a '+ 1)
(Na′+1)类分类器填补候选指数或空值来解码预测的参数(除候选论元表示
H
a
H_a
Ha外,附加了一个可学习的嵌入来表示空值)
P
r
o
l
e
=
s
o
f
t
m
a
x
(
t
a
n
h
(
H
e
2
r
W
1
+
H
a
W
2
)
⋅
v
1
)
P^{role}=softmax(tanh(H^{e2r}W_1+H^aW_2)\cdot v_1)
Prole=softmax(tanh(He2rW1+HaW2)⋅v1)其中,
W
1
∈
R
d
×
d
W_1∈\mathbb{R}^{d×d}
W1∈Rd×d,
W
2
∈
R
d
×
d
W_2∈\mathbb{R}^{d×d}
W2∈Rd×d,
v
1
∈
R
d
v_1∈\mathbb{R}^{d}
v1∈Rd都是可学习参数,
P
r
o
l
e
∈
R
m
×
d
×
(
N
a
′
+
1
)
P^{role}∈\mathbb{R}^{m×d×(N_a '+ 1)}
Prole∈Rm×d×(Na′+1)
在预测网络之后,得到了
m
m
m个事件,
Y
^
=
(
Y
^
1
,
Y
^
1
,
.
.
.
,
Y
^
m
)
\hat Y=(\hat Y_1,\hat Y_1,...,\hat Y_m)
Y^=(Y^1,Y^1,...,Y^m),其中,
Y
^
i
=
(
P
i
1
,
P
i
2
,
.
.
.
,
P
i
n
)
\hat Y_i=(P^1_i,P_i^2,...,P_i^n)
Y^i=(Pi1,Pi2,...,Pin)包含
n
n
n个预测论元,其中
P
i
j
=
P
r
o
l
e
[
i
,
j
,
:
]
∈
R
N
a
′
+
1
P_i^j =P^{role}[i,j,:]∈\mathbb{R}^{N_a'+1}
Pij=Prole[i,j,:]∈RNa′+1。
2.5 匹配损失
训练过程中,如何将预测的
m
m
m个事件和一系列论元指派给真实的
k
k
k个事件,受启发于匈牙利算法提出了匹配损失,可以在预测和真实事件间产生最优二分匹配。
预测事件(
m
m
m是固定的生成事件的数量):
Y
^
=
(
Y
^
1
,
Y
^
1
,
.
.
.
,
Y
^
m
)
\hat Y=(\hat Y_1,\hat Y_1,...,\hat Y_m)
Y^=(Y^1,Y^1,...,Y^m)
真实事件(
k
k
k是文档中的真实事件数量):
Y
=
(
Y
1
,
Y
2
,
.
.
.
,
Y
k
)
Y=(Y_1,Y_2,...,Y_k)
Y=(Y1,Y2,...,Yk)
m
≥
k
m≥k
m≥k,这里
m
m
m是2.4提到的超参数,在代码中表示为num_generated_sets。第
i
i
i个预测事件表示为
Y
^
i
=
(
P
i
1
,
P
i
2
,
.
.
.
,
P
i
n
)
\hat Y_i=(P^1_i,P_i^2,...,P_i^n)
Y^i=(Pi1,Pi2,...,Pin)。第
i
i
i个真实事件表示为
Y
i
=
(
r
i
1
,
r
i
2
,
.
.
.
,
r
i
n
)
Y_i=(r_i^1,r_i^2,...,r_i^n)
Yi=(ri1,ri2,...,rin)。
σ
^
=
arg
max
σ
∈
Π
(
m
)
∑
i
m
C
m
a
t
c
h
(
Y
^
σ
(
i
)
,
Y
i
)
\hat\sigma=\mathop{\arg\max}\limits_{\sigma\in\Pi(m)}\sum_{i}^mC_{match}(\hat Y_{\sigma(i)},Y_i)
σ^=σ∈Π(m)argmaxi∑mCmatch(Y^σ(i),Yi)
