AMP State Evolution的计算:以伯努利先验为例
AMP State Evolution (SE)的计算
t
=
1
t=1
t=1时,
E
(
t
)
=
E
[
X
2
]
\mathcal E^{(t)} = \mathbb E [X^2]
E(t)=E[X2],SE的迭代式为
τ
r
(
t
)
=
σ
2
+
1
δ
E
(
t
)
E
(
t
+
1
)
=
E
∣
η
(
t
)
(
X
+
Z
)
−
X
∣
2
,
Z
∼
N
(
0
,
τ
r
(
t
)
)
\begin{aligned} \tau^{(t)}_r &= \sigma^2 + \frac{1}{\delta} \mathcal E^{(t)} \\ \mathcal E^{(t+1)} &= \mathbb E \left | \eta^{(t)} \left ( X + Z \right) - X \right |^2, \ Z \sim \mathcal N(0, \tau^{(t)}_r) \end{aligned}
τr(t)E(t+1)=σ2+δ1E(t)=E
η(t)(X+Z)−X
2, Z∼N(0,τr(t))
撰写的时候存在一定的符号乱用,之后的 τ \tau τ即指 τ r ( t ) \tau^{(t)}_r τr(t)。
注意到,
E
(
t
+
1
)
=
E
∣
η
(
t
)
(
X
+
Z
)
−
X
∣
2
\mathcal E^{(t+1)} = \mathbb E \left | \eta^{(t)} \left ( X + Z \right) - X \right |^2
E(t+1)=E
η(t)(X+Z)−X
2是关于随机变量
X
,
Z
X, Z
X,Z求期望,这里我们认为
X
,
Z
X, Z
X,Z之间相互独立,因此
E
(
t
+
1
)
=
∫
∫
p
X
,
Z
(
X
,
Z
)
∣
η
(
t
)
(
X
+
Z
)
−
X
∣
2
d
X
d
Z
\mathcal E^{(t+1)} = \int \int p_{X, Z}(X, Z) \left | \eta^{(t)} \left ( X + Z \right) - X \right |^2 dX dZ
E(t+1)=∫∫pX,Z(X,Z)
η(t)(X+Z)−X
2dXdZ
令
R
=
X
+
Z
R = X + Z
R=X+Z,不难得到
p
X
,
R
(
X
,
R
)
p_{X, R}(X, R)
pX,R(X,R)等价于
p
X
,
Z
(
X
,
Z
)
p_{X, Z}(X, Z)
pX,Z(X,Z)(因为
p
X
,
Z
(
X
=
x
0
,
Z
=
z
0
)
=
p
X
,
R
(
X
=
x
0
,
R
=
x
0
+
z
0
)
p_{X, Z}(X=x_0, Z=z_0) = p_{X, R}(X=x_0, R=x_0 + z_0)
pX,Z(X=x0,Z=z0)=pX,R(X=x0,R=x0+z0)),因此我们可以把
E
(
t
+
1
)
\mathcal E^{(t+1)}
E(t+1)写为(这里我们考虑
η
(
t
)
\eta^{(t)}
η(t)为MMSE函数)
E
(
t
+
1
)
=
∫
∫
p
X
,
R
(
X
,
R
)
∣
η
(
t
)
(
R
)
−
X
∣
2
d
X
d
R
=
∫
∫
p
R
(
R
)
p
X
∣
R
(
X
∣
R
)
∣
E
[
X
∣
R
]
−
X
∣
2
d
X
d
R
=
∫
p
R
(
R
)
v
a
r
[
X
∣
R
]
d
R
\begin{aligned} \mathcal E^{(t+1)} &= \int \int p_{X, R}(X, R) \left | \eta^{(t)} \left ( R \right) - X \right |^2 dX dR \\ &= \int \int p_R(R) p_{X|R}(X|R) \left | \mathbb E\left [ X|R \right] - X \right |^2 dX dR \\ &= \int p_R(R) \mathrm{var}[X|R] dR \end{aligned}
E(t+1)=∫∫pX,R(X,R)
η(t)(R)−X
2dXdR=∫∫pR(R)pX∣R(X∣R)∣E[X∣R]−X∣2dXdR=∫pR(R)var[X∣R]dR
因为
p
X
,
Z
(
X
,
Z
)
=
p
X
(
X
)
⋅
p
X
(
Z
)
=
p
X
(
X
)
N
(
z
;
0
,
τ
r
(
t
)
)
p_{X, Z}(X, Z) = p_X(X) \cdot p_X(Z) = p_X(X) \mathcal N(z;0, \tau^{(t)}_r)
pX,Z(X,Z)=pX(X)⋅pX(Z)=pX(X)N(z;0,τr(t)),因此可以得到
p
X
,
R
(
X
,
R
)
=
p
X
(
X
)
N
(
R
−
X
;
0
,
τ
r
(
t
)
)
=
p
X
(
X
)
N
(
R
;
X
,
τ
r
(
t
)
)
\begin{aligned} p_{X, R}(X, R) &= p_X(X) \mathcal N(R-X;0, \tau^{(t)}_r) \\ &= p_X(X) \mathcal N(R;X, \tau^{(t)}_r) \end{aligned}
pX,R(X,R)=pX(X)N(R−X;0,τr(t))=pX(X)N(R;X,τr(t))
X的先验为为伯努利分布时
p X ( X ) ≡ ( 1 − ρ ) δ ( X ) + ρ δ ( X − θ ) p_X(X) \equiv (1-\rho) \delta(X) + \rho \delta(X - \theta) pX(X)≡(1−ρ)δ(X)+ρδ(X−θ)
那么,
X
,
R
X,R
X,R的联合分布可写为
p
X
,
R
(
X
,
R
)
=
(
(
1
−
ρ
)
δ
(
X
)
+
ρ
δ
(
X
−
θ
)
)
⋅
N
(
X
;
R
,
τ
r
(
t
)
)
=
(
1
−
ρ
)
δ
(
X
)
N
(
X
;
R
,
τ
r
(
t
)
)
+
ρ
δ
(
X
−
θ
)
N
(
X
;
R
,
τ
r
(
t
)
)
\begin{aligned} p_{X, R}(X, R) &= \left ((1-\rho) \delta(X) + \rho \delta(X - \theta) \right) \cdot \mathcal N(X;R, \tau^{(t)}_r) \\ &= (1-\rho) \delta(X) \mathcal N(X;R, \tau^{(t)}_r) + \rho \delta(X - \theta) \mathcal N(X;R, \tau^{(t)}_r) \end{aligned}
pX,R(X,R)=((1−ρ)δ(X)+ρδ(X−θ))⋅N(X;R,τr(t))=(1−ρ)δ(X)N(X;R,τr(t))+ρδ(X−θ)N(X;R,τr(t))
进一步,我们可以得到关于
R
R
R的边缘分布
p
R
(
R
)
=
∫
p
X
,
R
(
X
,
R
)
d
X
=
(
1
−
ρ
)
N
(
0
;
R
,
τ
r
(
t
)
)
+
ρ
N
(
θ
;
R
,
τ
r
(
t
)
)
=
(
1
−
ρ
)
N
(
R
;
0
,
τ
r
(
t
)
)
+
ρ
N
(
R
;
θ
,
τ
r
(
t
)
)
\begin{aligned} p_R(R) &= \int p_{X, R}(X, R) dX \\ &= (1-\rho) \mathcal N(0;R, \tau^{(t)}_r) + \rho \mathcal N(\theta;R, \tau^{(t)}_r) \\ &= (1-\rho) \mathcal N(R; 0, \tau^{(t)}_r) + \rho \mathcal N(R; \theta, \tau^{(t)}_r) \end{aligned}
pR(R)=∫pX,R(X,R)dX=(1−ρ)N(0;R,τr(t))+ρN(θ;R,τr(t))=(1−ρ)N(R;0,τr(t))+ρN(R;θ,τr(t))
我们计算后验均值
E
[
X
∣
R
]
\mathbb E[X|R]
E[X∣R]
E
[
X
∣
R
]
=
∫
X
p
X
∣
R
(
X
∣
R
)
d
X
=
1
p
R
(
R
)
∫
X
p
X
,
R
(
X
,
R
)
d
X
=
1
p
R
(
R
)
⋅
ρ
⋅
∫
X
δ
(
X
−
θ
)
N
(
X
;
R
,
τ
r
(
t
)
)
d
X
=
1
p
R
(
R
)
⋅
ρ
⋅
θ
⋅
N
(
R
;
θ
,
τ
r
(
t
)
)
=
θ
⋅
ρ
N
(
R
;
θ
,
τ
r
(
t
)
)
(
1
−
ρ
)
N
(
R
;
0
,
τ
r
(
t
)
)
+
ρ
N
(
R
;
θ
,
τ
r
(
t
)
)
=
θ
⋅
1
1
+
1
−
ρ
ρ
⋅
N
(
R
;
0
,
τ
r
(
t
)
)
N
(
R
;
θ
,
τ
r
(
t
)
)
=
θ
⋅
1
1
+
1
−
ρ
ρ
⋅
exp
{
−
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
\begin{aligned} \mathbb E[X|R] &= \int X p_{X|R} (X|R) dX \\ &= \frac{1}{p_R(R)} \int X p_{X,R} (X,R) dX \\ &= \frac{1}{p_R(R)} \cdot \rho \cdot \int X \delta(X - \theta) \mathcal N(X;R, \tau^{(t)}_r) dX \\ &= \frac{1}{p_R(R)} \cdot \rho \cdot \theta \cdot \mathcal N (R; \theta, \tau^{(t)}_r) \\ &= \theta \cdot \frac{ \rho \mathcal N (R; \theta, \tau^{(t)}_r) } {(1-\rho) \mathcal N(R; 0, \tau^{(t)}_r) + \rho \mathcal N(R; \theta, \tau^{(t)}_r) } \\ & = \theta \cdot \frac{ 1 } {1 + \frac{1-\rho}{\rho} \cdot \frac{ \mathcal N(R; 0, \tau^{(t)}_r) }{ \mathcal N(R; \theta, \tau^{(t)}_r) } } \\ &= \theta \cdot \frac{ 1 } {1 + \frac{1-\rho}{\rho} \cdot \exp \left \{\ - \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \} } \end{aligned}
E[X∣R]=∫XpX∣R(X∣R)dX=pR(R)1∫XpX,R(X,R)dX=pR(R)1⋅ρ⋅∫Xδ(X−θ)N(X;R,τr(t))dX=pR(R)1⋅ρ⋅θ⋅N(R;θ,τr(t))=θ⋅(1−ρ)N(R;0,τr(t))+ρN(R;θ,τr(t))ρN(R;θ,τr(t))=θ⋅1+ρ1−ρ⋅N(R;θ,τr(t))N(R;0,τr(t))1=θ⋅1+ρ1−ρ⋅exp{ −2τr(t)2θR−θ2}1
同理可得,
E
[
X
2
∣
R
]
=
θ
⋅
E
[
X
∣
R
]
\mathbb E[X^2|R] = \theta \cdot \mathbb E[X|R]
E[X2∣R]=θ⋅E[X∣R]
因此
v
a
r
[
X
∣
R
]
=
E
[
X
2
∣
R
]
−
E
[
X
∣
R
]
2
\mathrm{var}[X|R] = \mathbb E[X^2|R] - \mathbb E[X|R]^2
var[X∣R]=E[X2∣R]−E[X∣R]2
令
ψ
(
R
)
=
1
−
ρ
ρ
⋅
exp
{
−
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
\psi(R) =\frac{1-\rho}{\rho} \cdot \exp \left \{\ - \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \}
ψ(R)=ρ1−ρ⋅exp{ −2τr(t)2θR−θ2},则
v
a
r
[
X
∣
R
]
\mathrm{var}[X|R]
var[X∣R]可写为
v
a
r
[
X
∣
R
]
=
θ
2
1
2
+
ψ
(
R
)
+
1
ψ
(
R
)
=
θ
2
1
2
+
1
−
ρ
ρ
⋅
exp
{
−
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
+
ρ
1
−
ρ
exp
{
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
\begin{aligned} \mathrm{var}[X|R] &= \theta^2 \frac{1}{ 2+ \psi(R) + \frac{1}{\psi(R) }} \\ &= \theta^2 \frac{1} { 2 + \frac{1- \rho}{\rho} \cdot \exp \left \{\ - \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \} +\frac{\rho}{1-\rho} \exp \left \{\ \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \}} \end{aligned}
var[X∣R]=θ22+ψ(R)+ψ(R)11=θ22+ρ1−ρ⋅exp{ −2τr(t)2θR−θ2}+1−ρρexp{ 2τr(t)2θR−θ2}1
进一步,
E
(
t
+
1
)
\mathcal E^{(t+1)}
E(t+1)可以表征为
E
(
t
+
1
)
=
∫
p
R
(
R
)
v
a
r
[
X
∣
R
]
d
R
=
θ
2
∫
1
2
+
1
−
ρ
ρ
⋅
exp
{
−
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
+
ρ
1
−
ρ
⋅
exp
{
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
(
(
1
−
ρ
)
N
(
R
;
0
,
τ
r
(
t
)
)
+
ρ
N
(
R
;
θ
,
τ
r
(
t
)
)
)
d
R
\begin{aligned} \mathcal E^{(t+1)} &= \int p_R(R) \mathrm{var}[X|R] dR \\ &= \theta^2 \int \frac{1} { 2 + \frac{1- \rho}{\rho} \cdot \exp \left \{\ - \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \} + \frac{\rho}{1-\rho} \cdot \exp \left \{\ \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \}} \left ( (1-\rho) \mathcal N(R; 0, \tau^{(t)}_r) + \rho \mathcal N(R; \theta, \tau^{(t)}_r) \right ) dR \end{aligned}
E(t+1)=∫pR(R)var[X∣R]dR=θ2∫2+ρ1−ρ⋅exp{ −2τr(t)2θR−θ2}+1−ρρ⋅exp{ 2τr(t)2θR−θ2}1((1−ρ)N(R;0,τr(t))+ρN(R;θ,τr(t)))dR
总结
t
=
1
t=1
t=1时,
E
(
t
)
=
E
[
X
2
]
\mathcal E^{(t)} = \mathbb E [X^2]
E(t)=E[X2],SE的迭代式为
τ
r
(
t
)
=
σ
2
+
1
δ
E
(
t
)
E
(
t
+
1
)
=
E
∣
η
(
t
)
(
X
+
Z
)
−
X
∣
2
,
Z
∼
N
(
0
,
τ
r
(
t
)
)
\begin{aligned} \tau^{(t)}_r &= \sigma^2 + \frac{1}{\delta} \mathcal E^{(t)} \\ \mathcal E^{(t+1)} &= \mathbb E \left | \eta^{(t)} \left ( X + Z \right) - X \right |^2, \ Z \sim \mathcal N(0, \tau^{(t)}_r) \end{aligned}
τr(t)E(t+1)=σ2+δ1E(t)=E
η(t)(X+Z)−X
2, Z∼N(0,τr(t))
当
X
X
X的先验是伯努利时:
X
∼
(
1
−
ρ
)
δ
(
X
)
+
ρ
δ
(
X
−
θ
)
X \sim (1-\rho) \delta(X) + \rho \delta(X - \theta)
X∼(1−ρ)δ(X)+ρδ(X−θ),可以把SE表征为
t
=
1
t=1
t=1时,
E
(
t
)
=
E
[
X
2
]
=
ρ
ν
\mathcal E^{(t)} = \mathbb E [X^2]= \rho \nu
E(t)=E[X2]=ρν,SE的迭代式为
τ
r
(
t
)
=
σ
2
+
1
δ
E
(
t
)
E
(
t
+
1
)
=
θ
2
∫
1
2
+
1
−
ρ
ρ
⋅
exp
{
−
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
+
ρ
1
−
ρ
⋅
exp
{
2
θ
R
−
θ
2
2
τ
r
(
t
)
}
(
(
1
−
ρ
)
N
(
R
;
0
,
τ
r
(
t
)
)
+
ρ
N
(
R
;
θ
,
τ
r
(
t
)
)
)
d
R
\begin{aligned} \tau^{(t)}_r &= \sigma^2 + \frac{1}{\delta} \mathcal E^{(t)} \\ \mathcal E^{(t+1)} &= \theta^2 \int \frac{1} { 2 + \frac{1- \rho}{\rho} \cdot \exp \left \{\ - \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \} + \frac{\rho}{1-\rho} \cdot \exp \left \{\ \frac{ 2 \theta R - \theta^2 }{2 \tau^{(t)}_r } \right \}} \left ( (1-\rho) \mathcal N(R; 0, \tau^{(t)}_r) + \rho \mathcal N(R; \theta, \tau^{(t)}_r) \right ) dR \end{aligned}
τr(t)E(t+1)=σ2+δ1E(t)=θ2∫2+ρ1−ρ⋅exp{ −2τr(t)2θR−θ2}+1−ρρ⋅exp{ 2τr(t)2θR−θ2}1((1−ρ)N(R;0,τr(t))+ρN(R;θ,τr(t)))dR
SE部分的MATLAB代码
Iteration = 40;
sigma2 = 0.2632;
rho = 0.1; % sparsity
v_g = 1 / rho; % variance/energy of the non-zero element (prior)
theta = sqrt(v_g);
delta = 0.6; % under-determined ratio
lim = inf;
SE_MSE = zeros(Iteration, 1);
SE_tau2 = zeros(Iteration, 1);
SE_MSE(1) = rho * v_g;
SE_tau2(1) = sigma2 + 1/delta * SE_MSE(1);
bound = 500;
fb = @(b) (b > bound) .* bound + (b < -bound) .* (-bound) + (abs(b) <= bound) .* b; % bound < f(b) < bound
for it = 2: Iteration
tau = SE_tau2( it - 1 );
f = @(r) 1 ./ ...
( 2 + (1-rho)./rho .* exp( fb(-0.5 * ( 2 * theta .* r - theta .* theta) / tau ) ) + rho./(1-rho) .* exp( fb(0.5 * ( 2 * theta .* r - theta .* theta) / tau )) ) ...
.* ( (1-rho) .* normpdf(r, 0, sqrt(tau)) + rho .* normpdf(r, theta, sqrt(tau)) );
SE_MSE(it) = theta^2 * integral(f,-lim,lim);
SE_tau2(it) = sigma2 + 1/delta * SE_MSE(it);
end
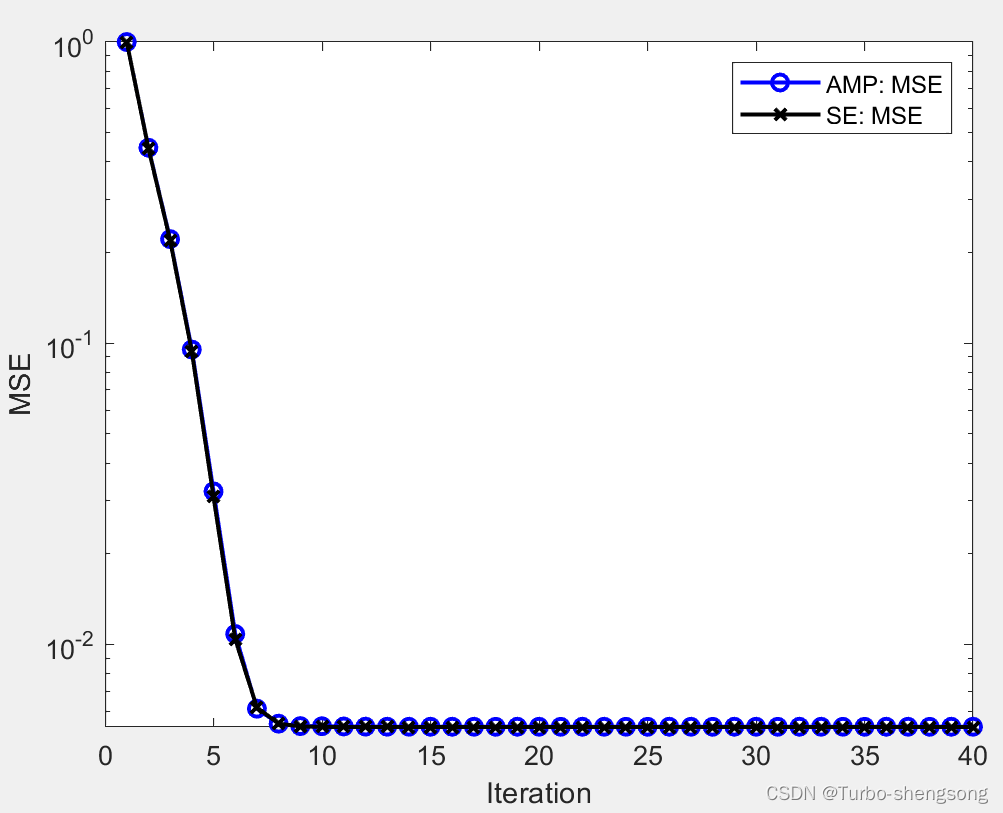
当N=40000时,AMP的MSE性能与SE一致