算法刷题-动态规划3(未完待续---------

01背包问题

一篇文章吃透背包问题
大佬讲解什么是背包问题

问题分析：
面对这么多的物品，
选择一个个地来装入背包，背包的承重量不断地增加，二维数组中，列为物品i，行为背包的承重量)。
当物品 i 的重量大于背包当前的总承重时，该物品不能放入背包；
当物品 i 的重量小于背包的总承重时，我们就要进行对比，前面 i - 1个物品所带来的价值和现在要取出背包中
的一部分物品用来存放物品i带来的价值，哪个更大？（取出多少呢，当然是刚好能放下物品 i 的重量，即w[i]），
把更大的那个价值对当前背包价值进行更新。

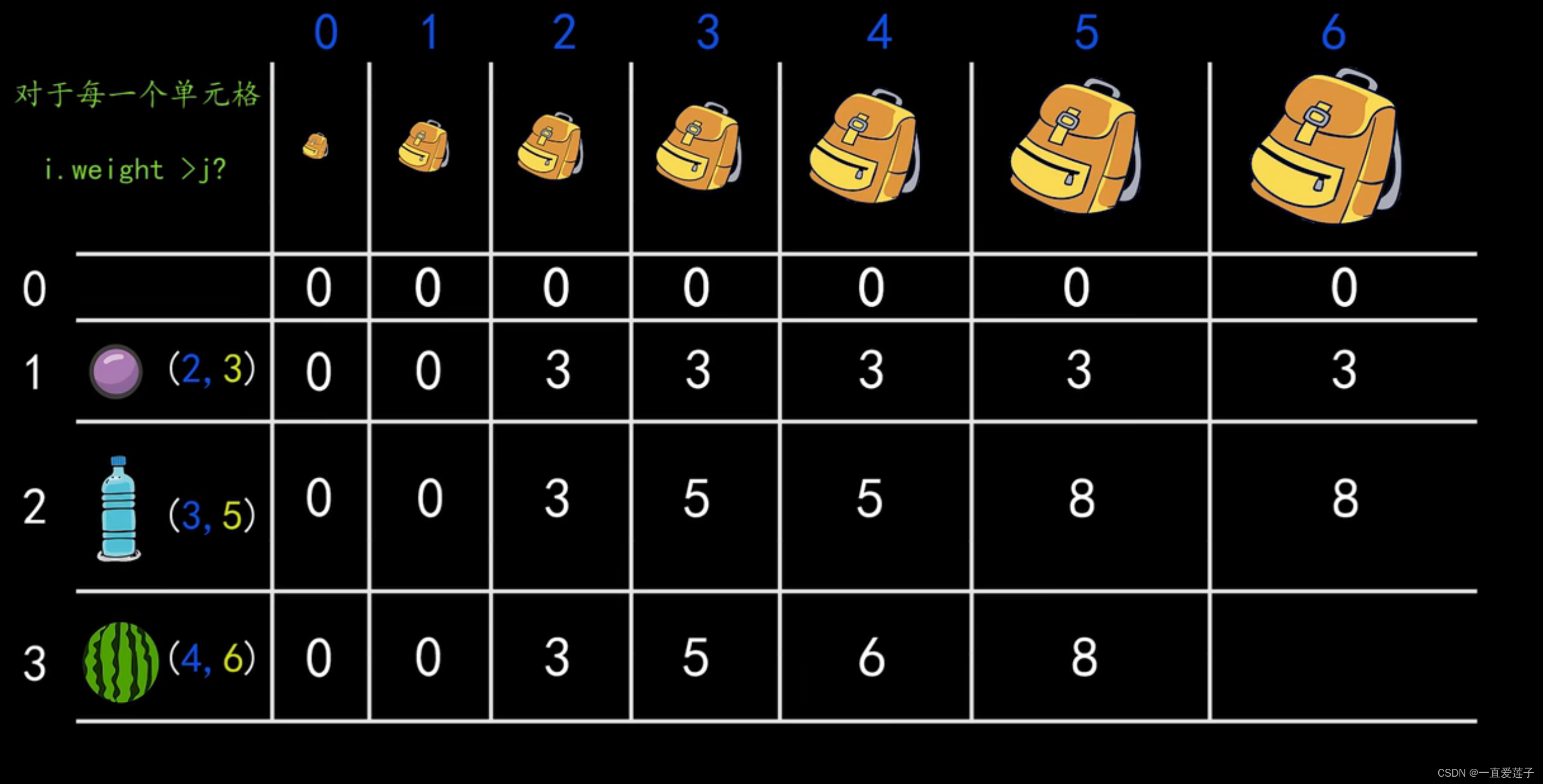
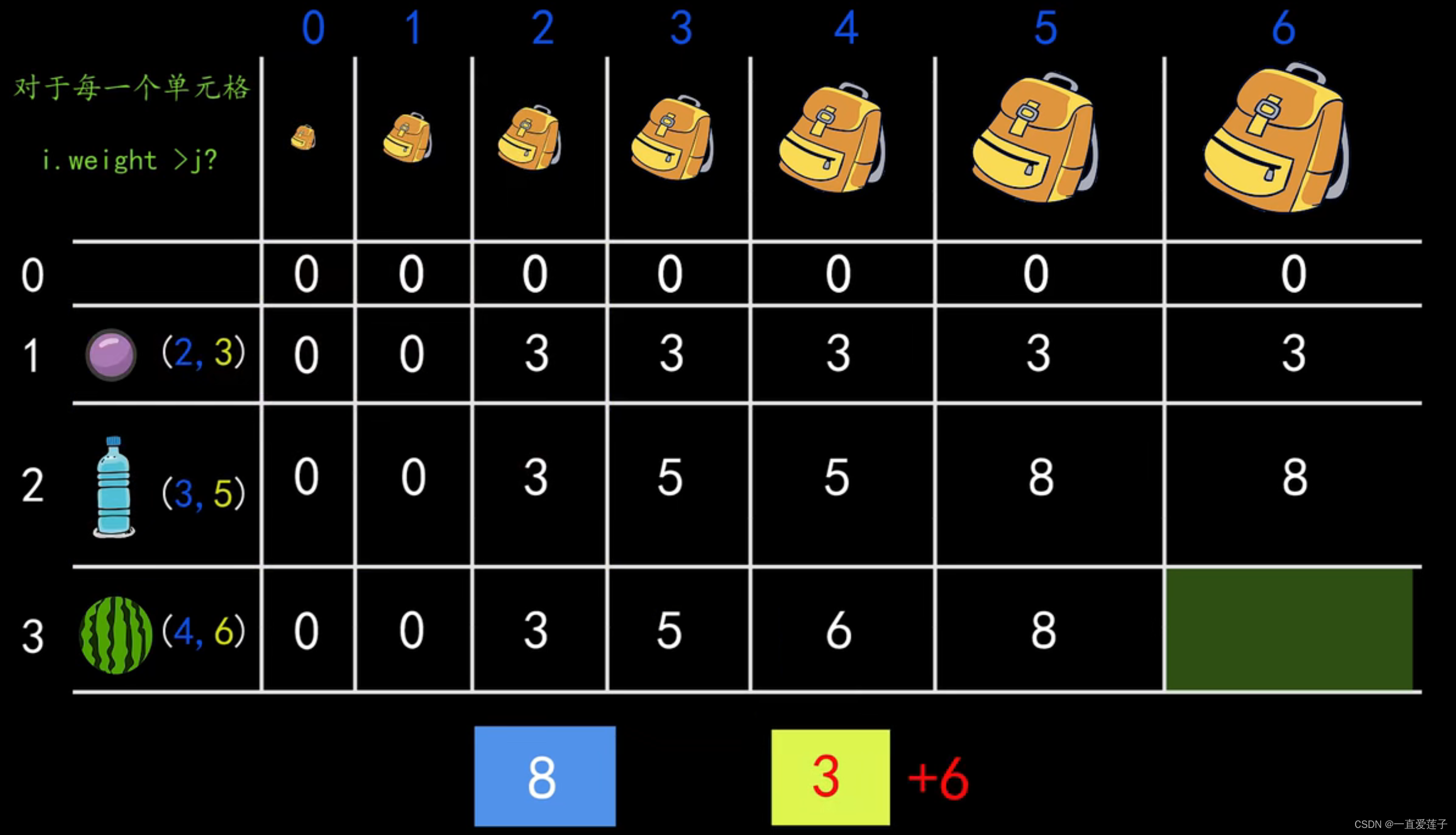
• arr[ i ][ j ] = max(arr[ i - 1 ][ j ], arr[ i - 1][ j - w[ i ] ] + v[ i ])
  

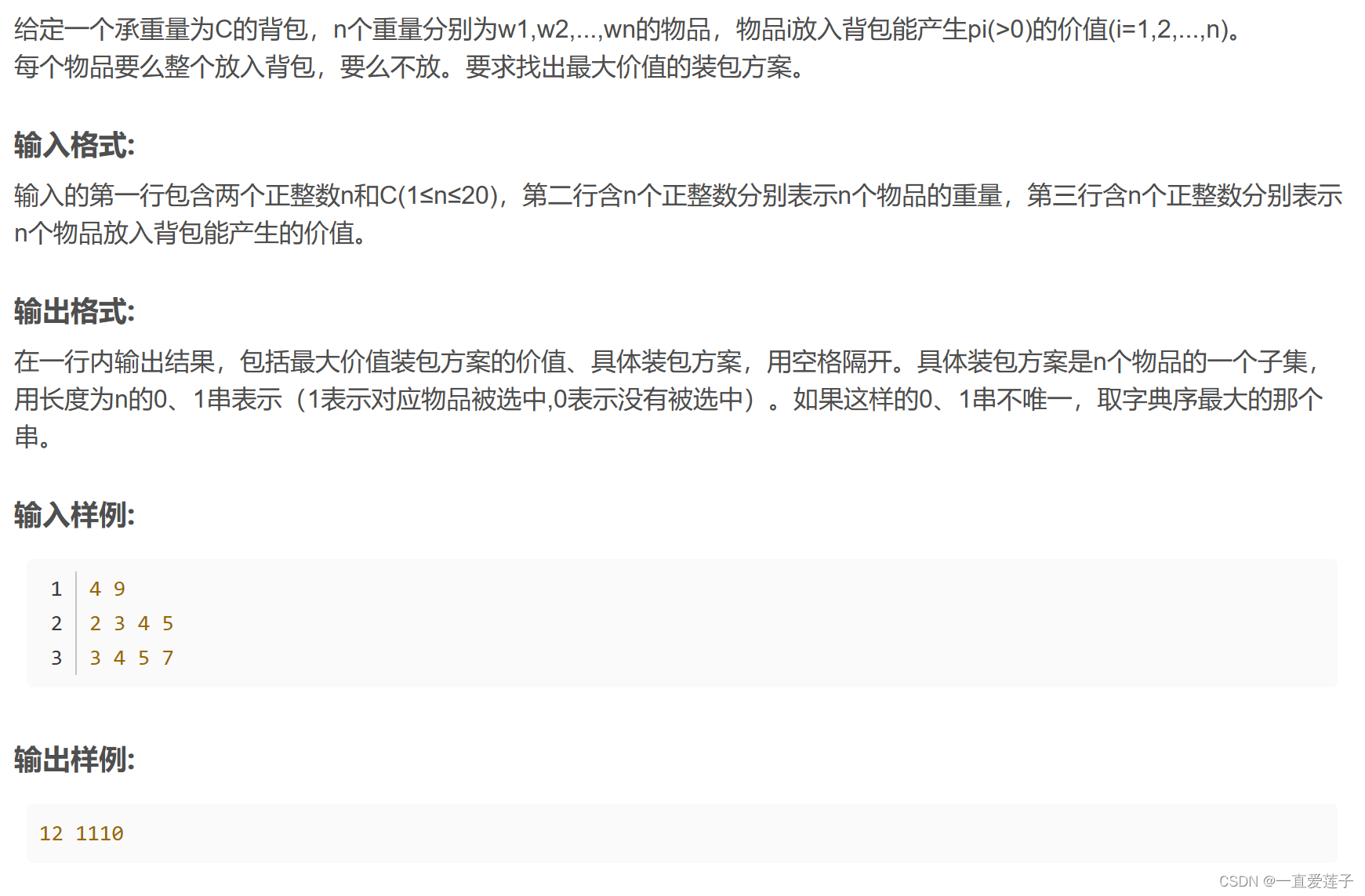
for(int i=1;i<=n;i++)//物品i 
{
	for(int j=1;j<=c;j++)//重量j 
	{
		if(j>=w[i])
		{
			arr[i][j]=max(arr[i-1][j],arr[i-1][j-w[i]]+v[i]);	
		}
		else arr[i][j]=arr[i-1][j];
	}
}

public static int knapsack(int[] C, int[] W, int V, int N) {
    // 初始化dp数组，dp[i][j]表示前i个物品，背包容量为j时的最大价值
    int[][] dp = new int[N + 1][V + 1];
    
    // 当背包容量为0时，无论有多少物品，最大价值都为0
    for (int i = 0; i <= N; i++) {
        dp[i][0] = 0;
    }
    
    // 当没有物品可选时，无论背包容量有多少，最大价值都为0
    for (int j = 0; j <= V; j++) {
        dp[0][j] = 0;
    }
 
    // 填充dp数组，从前往后遍历每个物品，从小到大遍历背包容量
    for (int i = 1; i <= N; i++) {
        for (int j = 1; j <= V; j++) {
            // 如果当前物品的重量小于等于背包容量，可以考虑将其放入背包
            if (j >= W[i - 1]) {
                // 如果放入当前物品，可以得到的最大价值比不放入当前物品的最大价值更高，则放入当前物品
                dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - W[i - 1]] + C[i - 1]);
            } else {
                // 如果当前物品的重量大于背包容量，无法放入背包，最大价值等于上一个物品的最大价值  
                dp[i][j] = dp[i - 1][j];  
            }
        }
    }
 
    // 返回最大价值，即dp[N][V]  
    return dp[N][V];  
}

分割等和子集

（待回顾和复习）美好的一天从每日一题开死

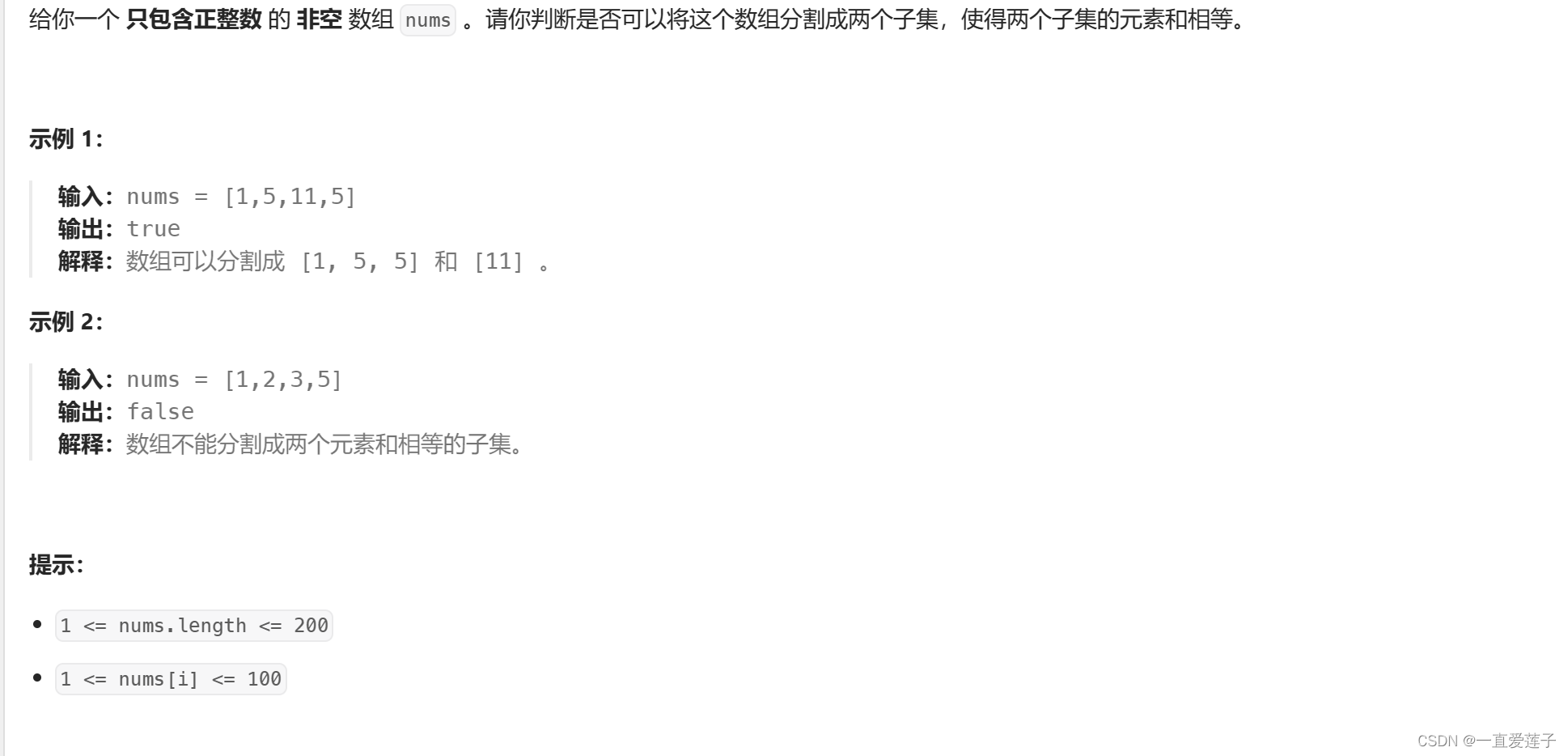
题目讲解

class Solution {
    //看不懂先去看二维数组解法
    public boolean canPartition(int[] nums) {
        int len=nums.length;  
        int sum=0;  
        for(int i=0;i<len;i++){  
            sum+=nums[i];  
        }
        if(sum%2!=0) return false;  
        //背包容量为总和的一半  
        int target=sum/2;  
        //dp[j]:容量为j时可放入物品的最大价值  
        int[] dp=new int[target+1];  
        for(int i=0;i<len;i++){  
            for(int j=target;j>=nums[i];j--){  
                dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);  
            }
        }
        return dp[target]==target;  
    }
}

最后一块石头的重量