高等数学零基础篇复习笔记
预备章 零基础高等数学入门知识
第一节 集合、运算与关系

第二节 三角函数与反三角函数
三角函数的公式
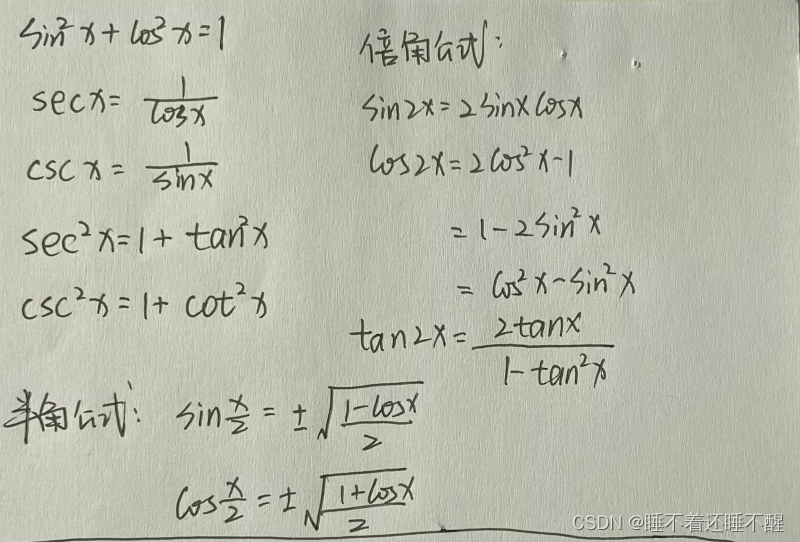
反三角函数
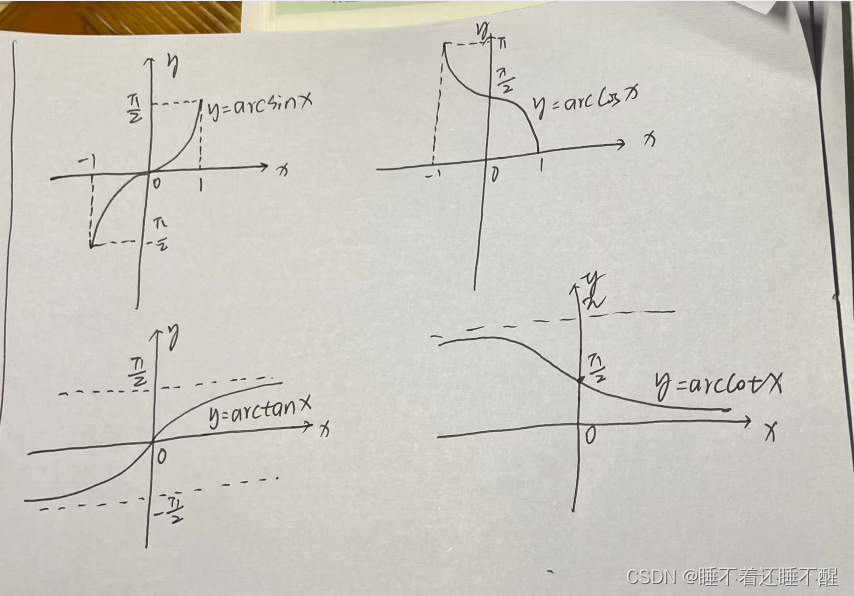
第三节 常见不等式及数列

划重点
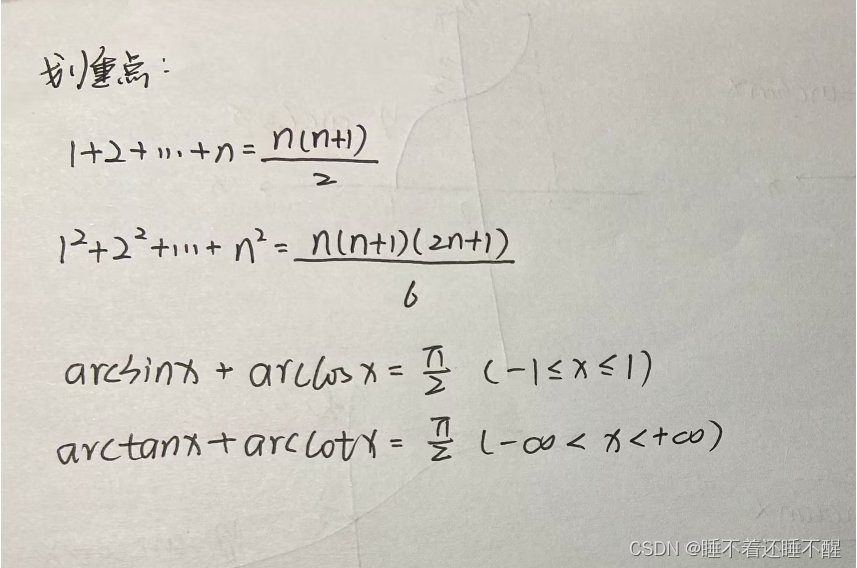
第一章 函数、极限与连续
第一节 函数及函数的初等特性
特殊函数

反函数

函数的初等特性
①有界性
②奇偶性
偶函数图像关于y轴对称,奇函数图像关于原点对称
奇函数与偶函数之积为奇函数,奇函数与奇函数之积为偶函数
③单调性
④周期性
第二节 极限
基本性质
极限存在的充要条件是左右极限存在且相等

极限的基本性质
定理一(唯一性):无论是数列极限还是函数关于自变量各种趋向,若极限存在必唯一

定理二(有界性):极限存在必有界,反之不成立

定理三(保号性):

证明如下:

第三节 无穷小与无穷大
基本概念

无穷小的基本性质
1.有限个无穷小之和或差仍为无穷小
2.有界函数与无穷小之积仍为无穷小
3.常数与无穷小之积仍为无穷小
4.极限与无穷小的关系:
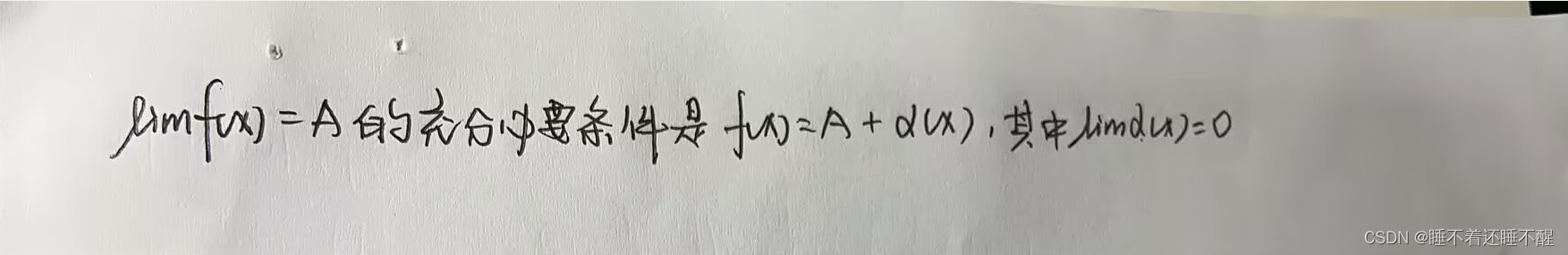
协助证明:

无穷小的等价性质

第四节 极限存在准则与重要极限
极限存在定理
夹逼定理
定理:

证明:

例题:


单调有界定理

例题:


两个重要极限

例题: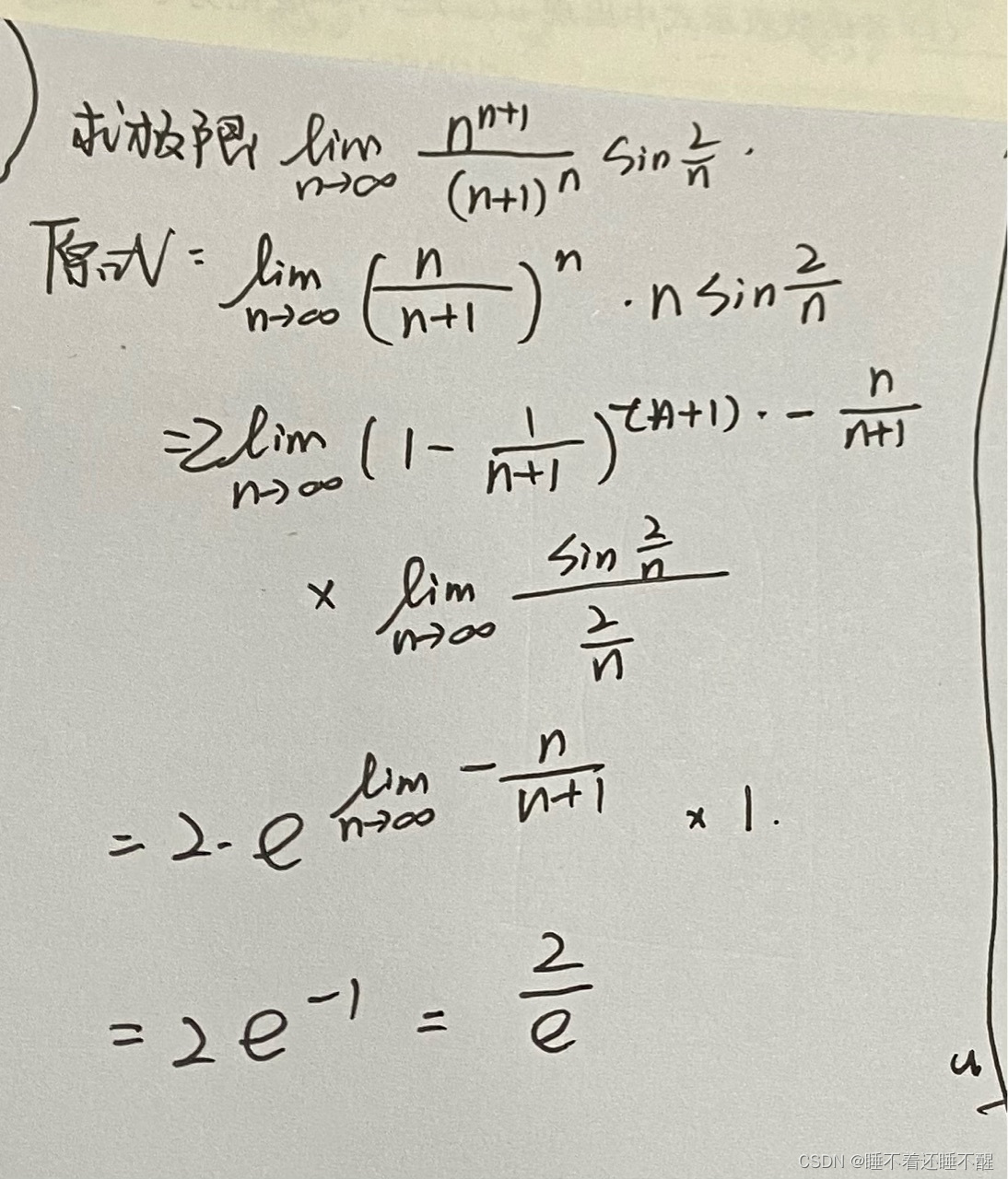
第五节 连续与间断
连续

间断

闭区间上连续函数的性质

章节重点习题
题型一 不定型极限计算

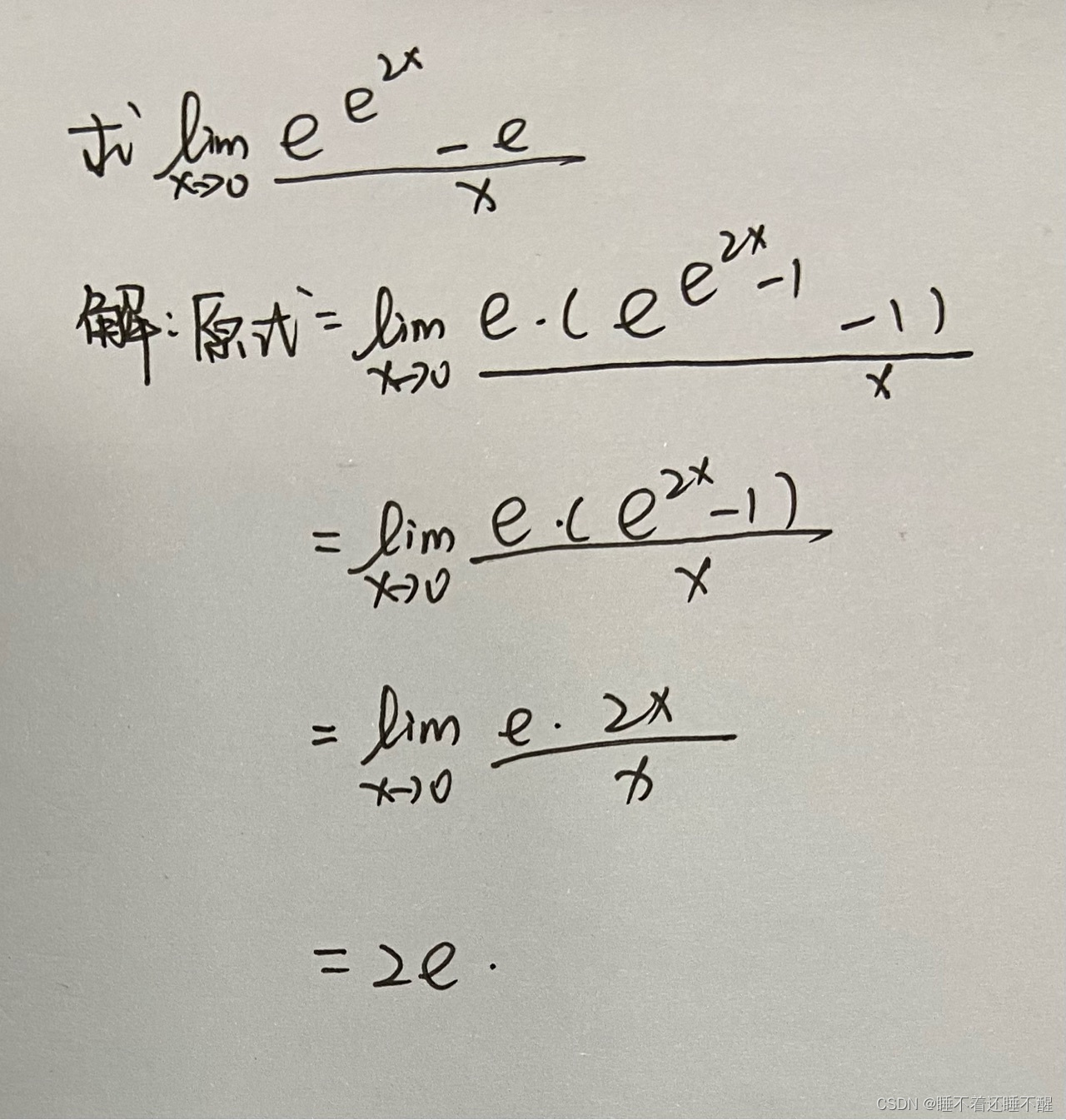
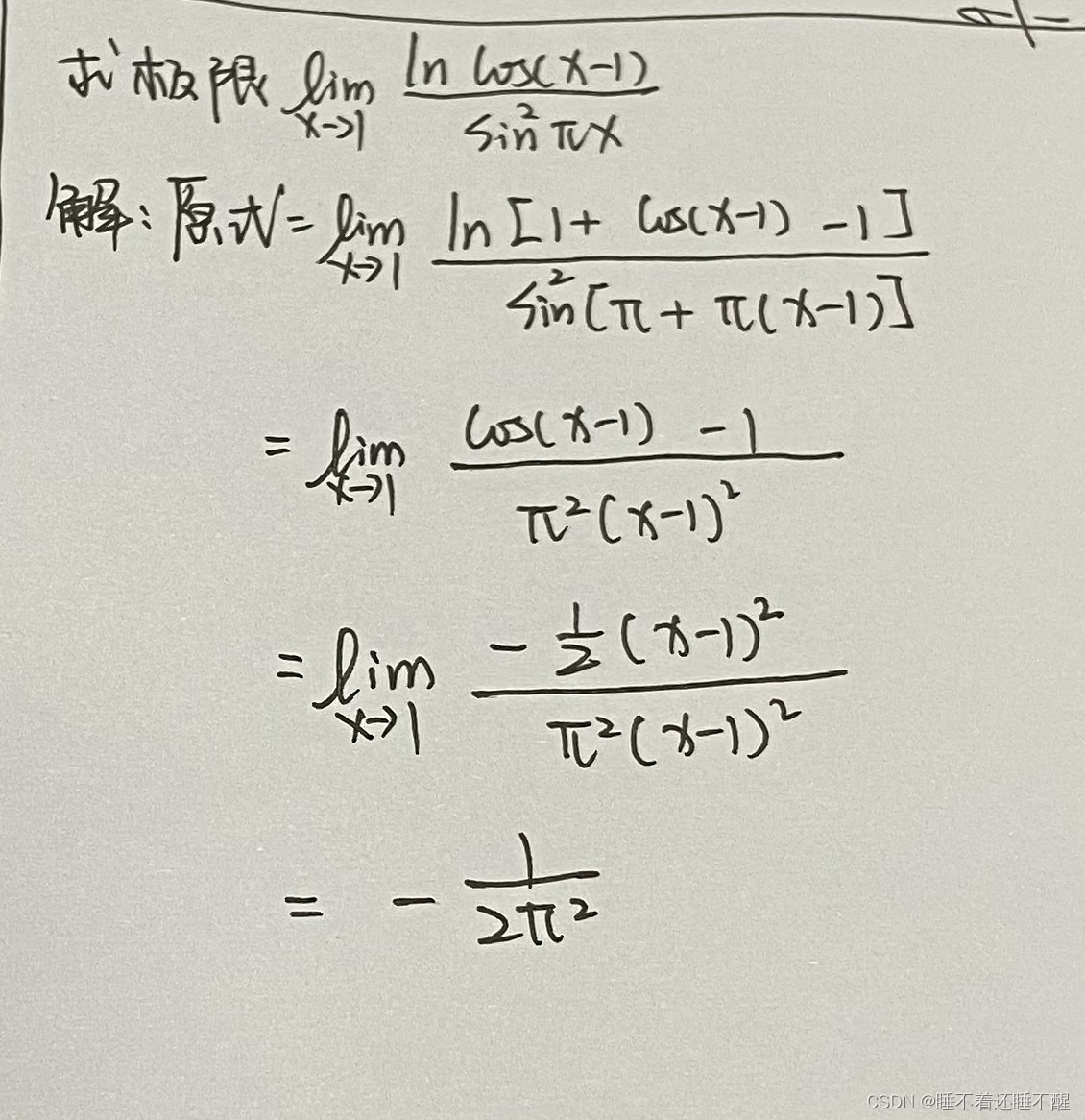




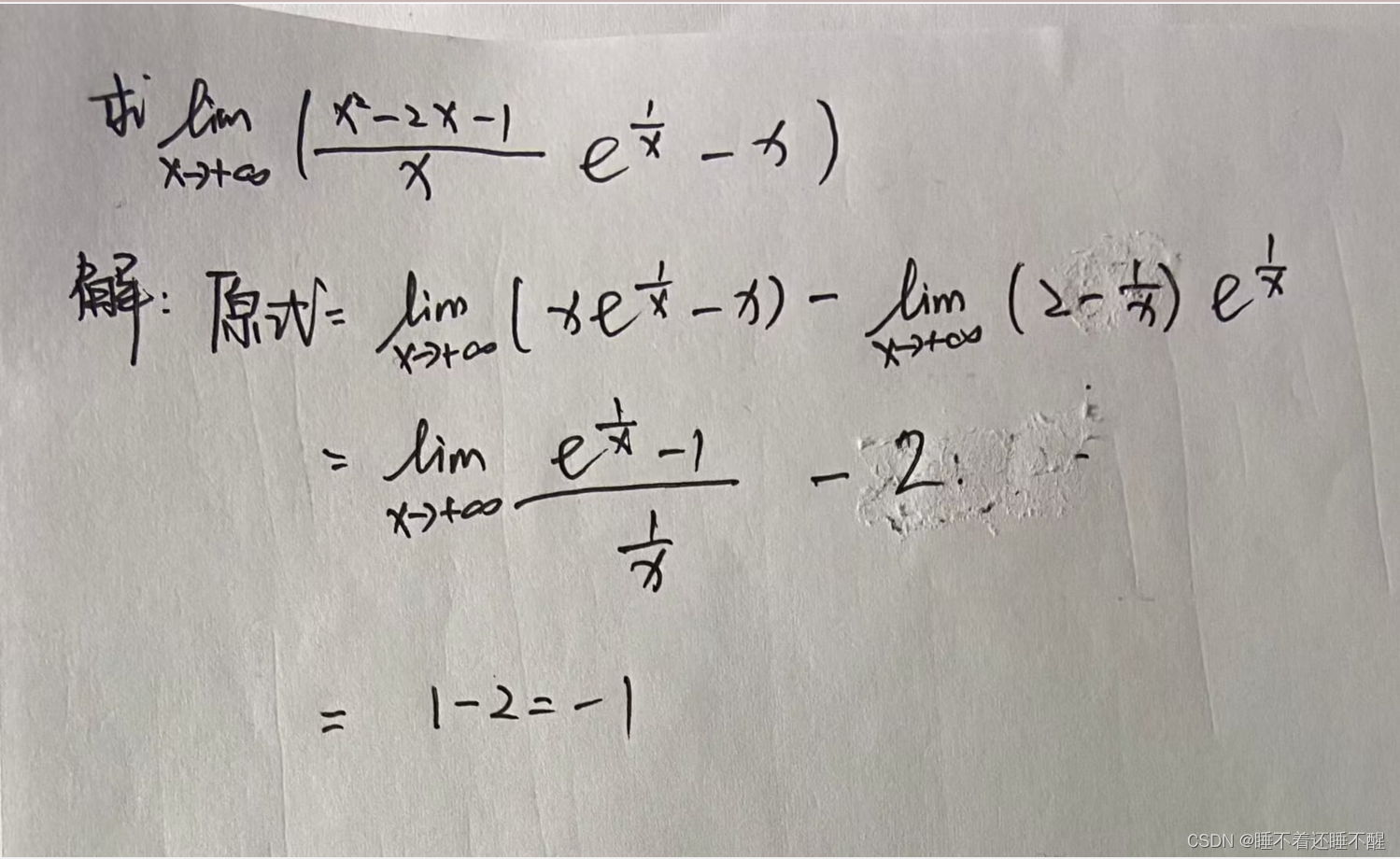
题型二 利用夹逼定理求极限
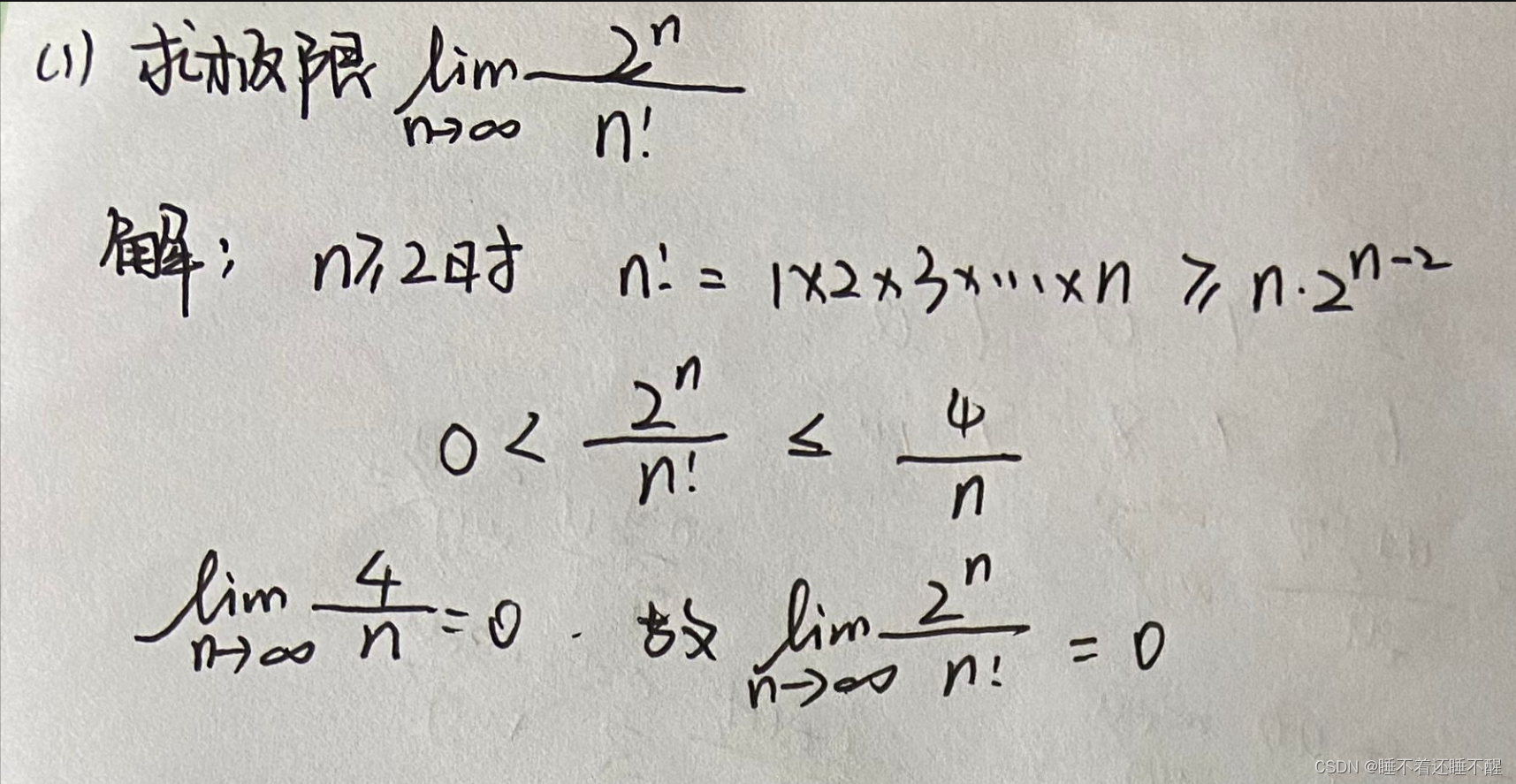
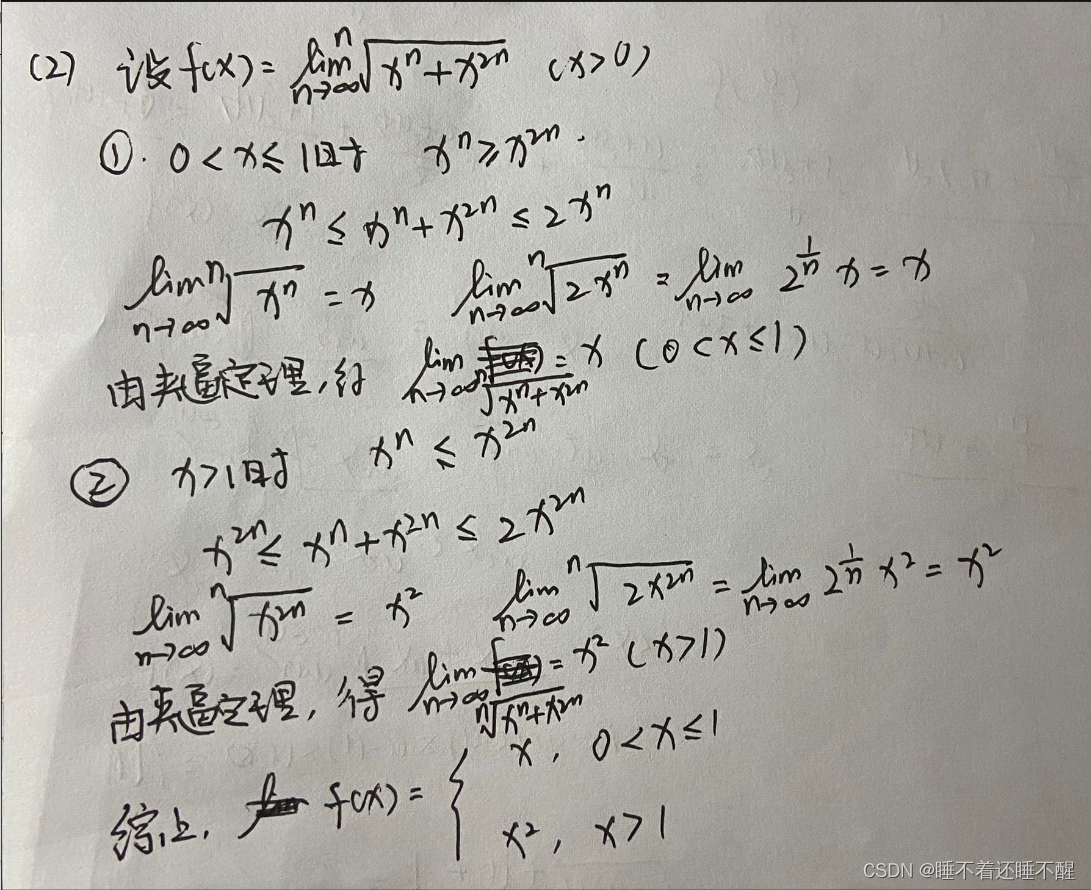
题型三 无穷小的比较


题型四 间断点判断

第二章 导数与微分
第一节 导数与微分的基本概念与性质
基本概念
导数:

微分:
函数f(x)在点x处可导的充要条件为f(x)在点x可微
求导基本工具
求导基本公式:
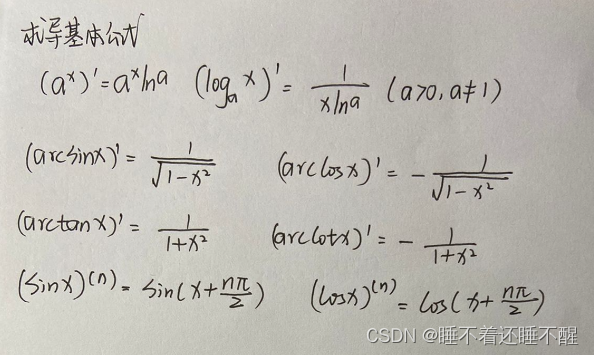
导数的四则运算:

链式法则:

反函数的导数:

第二节 隐函数及参数方程确定的函数的导数
隐函数的导数
F(x,y)=0确定y是x的函数,求y对x的各阶导数,只要将y看成x的表达式即可。
参数方程确定的函数的导数

章节重点习题
题型一 用导数定义求导及判断可导性


第三章 中值定理与导数的应用
第一节 中值定理与洛必达法则
费马定理

罗尔定理

拉格朗日中值定理

柯西中值定理

泰勒定理

常见麦克劳林公式:
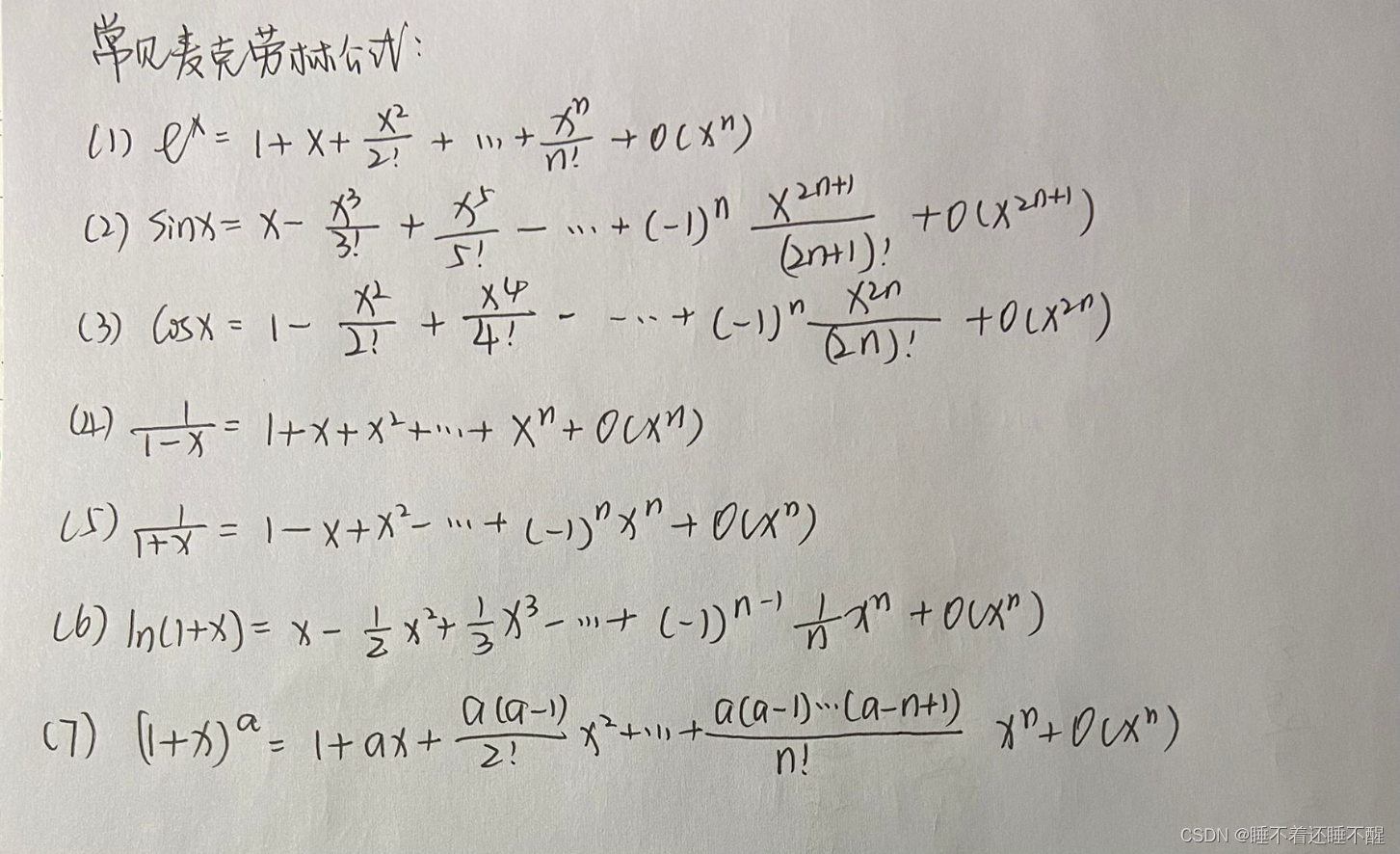
补充例题:构造函数证明等式


洛必达法则
适用情况:零比零型、无穷比无穷型
说明:使用洛必达法则后没有极限,只能说明洛必达法则对该题不适用,不能说明极限不存在
基本原理:分子分母同时求导得到的极限等于原分子比分母的极限
第二节 导数的应用
求函数极值点的步骤
注明:首先要看定义域

极值判定定理第二充分条件

函数图像的凹凸性

凹凸性判别法:

判别法证明:

曲线的渐近线

弧微分与曲率

章节重点习题
题型一 中值定理及应用


题型二 不等式的证明

题型三 曲线的渐近线

第四章 不定积分
第一节 不定积分的基本概念与性质
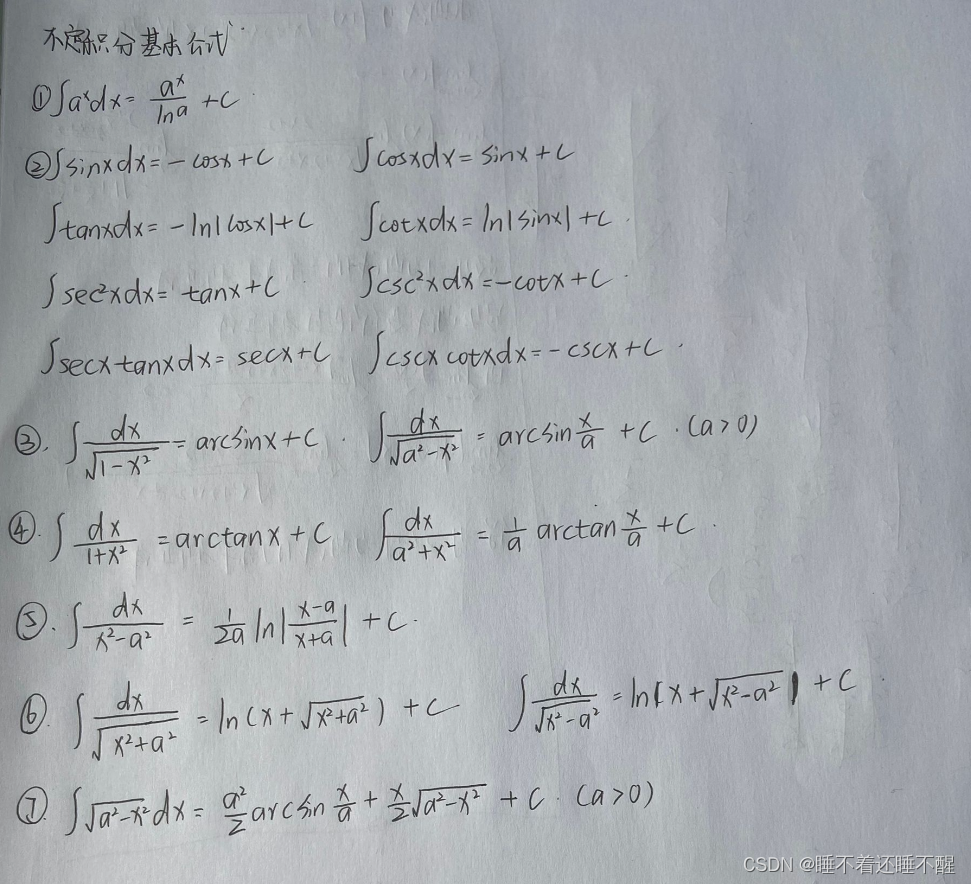
第二节 不定积分的积分法
第一类换元积分
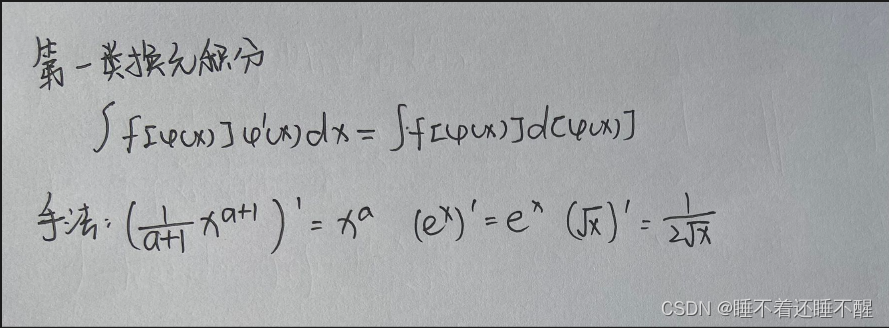
典型例题:

第二类换元积分

典型例题:

分部积分法

第三节 两类特殊函数的不定积分
有理函数的不定积分

多项式的除法:

三角函数有理式的不定积分

典型例题:

章节重点习题
题型一 函数与原函数问题

题型二 第一类换元积分法

题型三 第二类换元积分法

第五章 定积分及应用
第一节 定积分的基本概念与一般性质

积分中值定理的证明:

tips:

第二节 定积分基本定理与定积分的特殊性质
变积分限的函数

定积分的基本定理
定理一:

划重点:

定理二:

定积分的特殊性质
对称区间的定积分性质

三角函数的定积分性质


周期函数的定积分性质

第三节 反常积分
反常积分的定义

区间无限的反常积分




无界函数的反常积分



第四节 定积分的几何应用
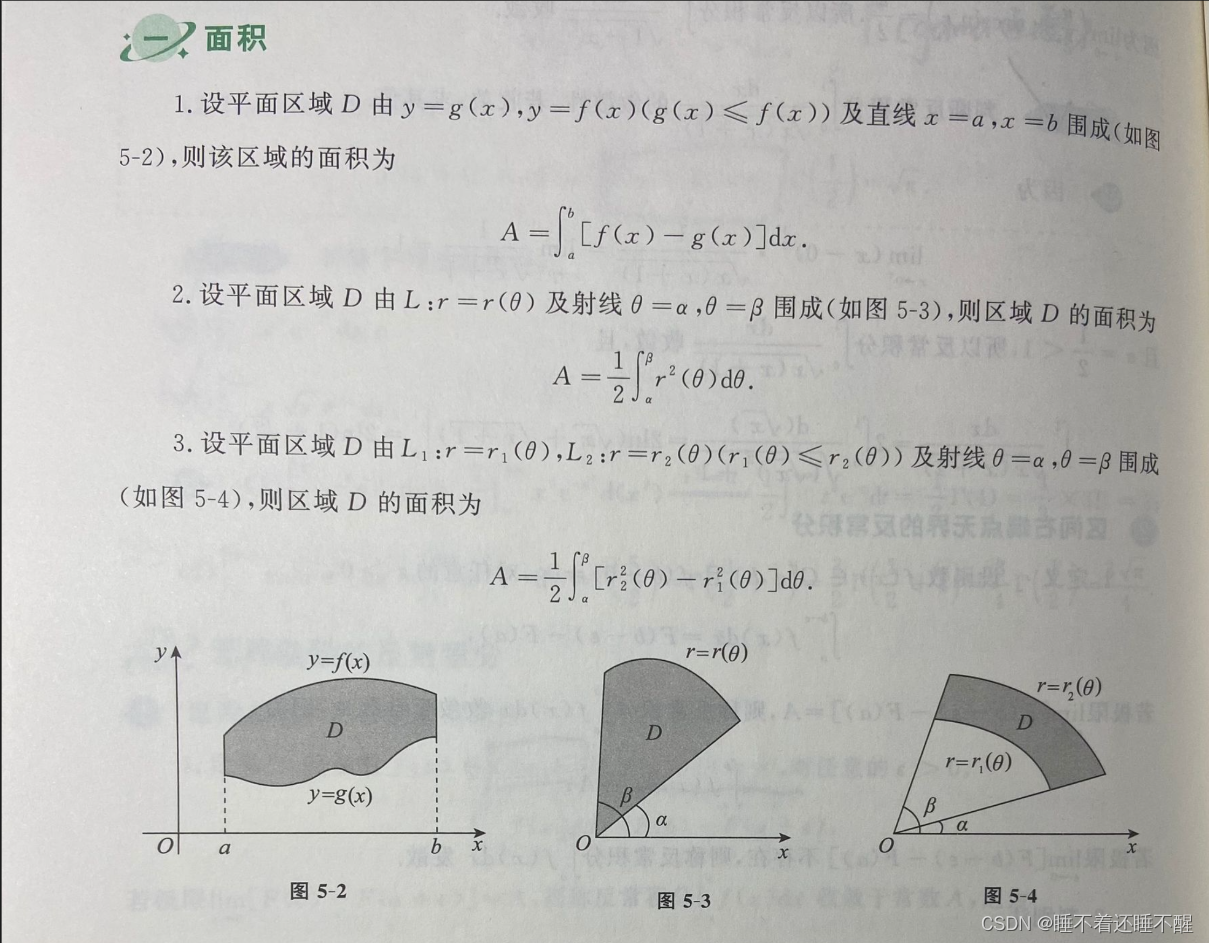

章节重点习题
题型一 定积分的基本性质

题型二 定积分的常规计算
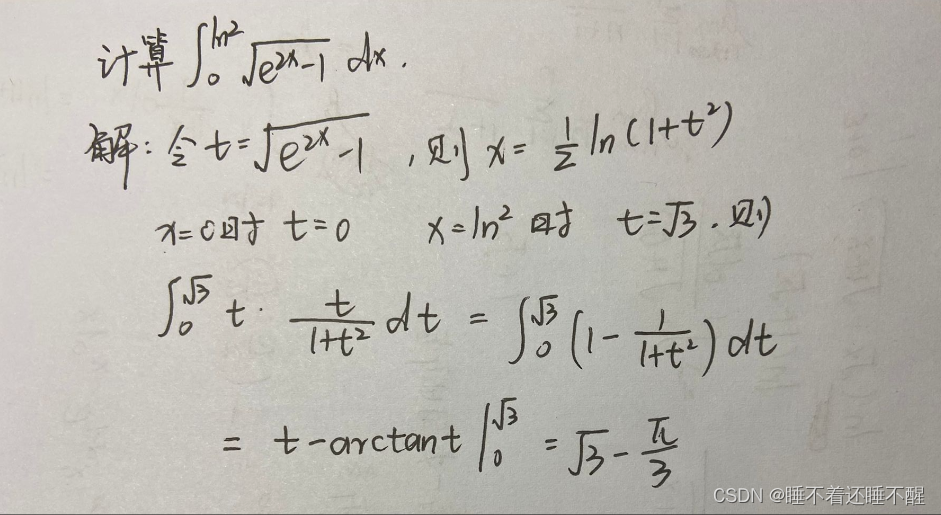
第六章 微分方程
第一节 微分方程的基本概念与一阶微分方程
微分方程的基本概念

划重点:

一阶微分方程的种类及解法
可分离变量的微分方程

齐次微分方程

一阶齐次线性微分方程

一阶非齐次线性微分方程

第二节 可降阶的高阶微分方程
情况一:

情况二:

情况三:

第三节 高阶线性微分方程
基本概念

二阶线性微分方程的解的结构

二阶常系数线性微分方程的解
二阶常系数齐次线性微分方程

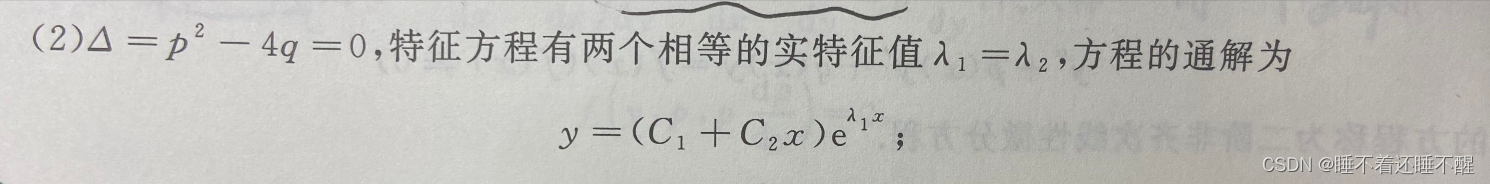

二阶常系数非齐次线性微分方程



第七章 多元函数微分学
第一节 多元函数微分学的基本概念
偏导数

高阶偏导数

有界闭区域上二元连续函数的性质

第二节 全微分
全微分的定义

划重点:

二元函数连续、可偏导、可微之间的关系
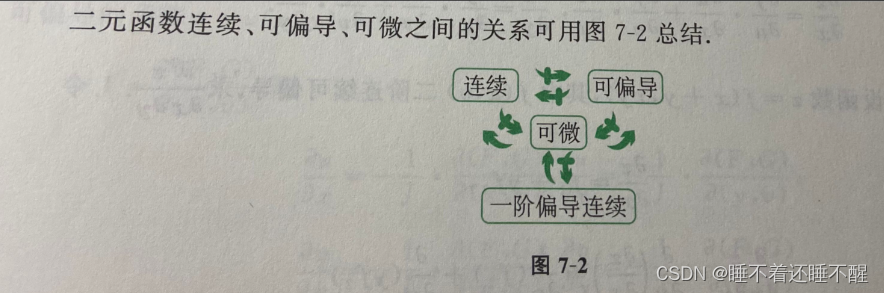
第三节 多元函数求导法则
复合函数求导法则

隐函数(组)确定的函数求导法则


第四节 多元函数的极值
无条件极值

条件极值

章节重点习题
题型一 多元函数的基本概念与性质

题型二 显函数、复合函数及隐函数求偏导

题型三 多元函数的极值


第八章 二重积分
第一节 二重积分的概念与性质

二重积分的对称性

章节重点习题

高等数学零基础篇复习到此结束,祝各位友友一战成硕~~
