爬楼梯（力扣LeetCode）动态规划

爬楼梯

题目描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。

1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。

1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：

1 <= n <= 45

动规五部曲：

定义⼀个⼀维数组来记录不同楼层的状态

1. 确定dp数组以及下标的含义
   dp[i]： 爬到第i层楼梯，有dp[i]种⽅法
2. 确定递推公式
   
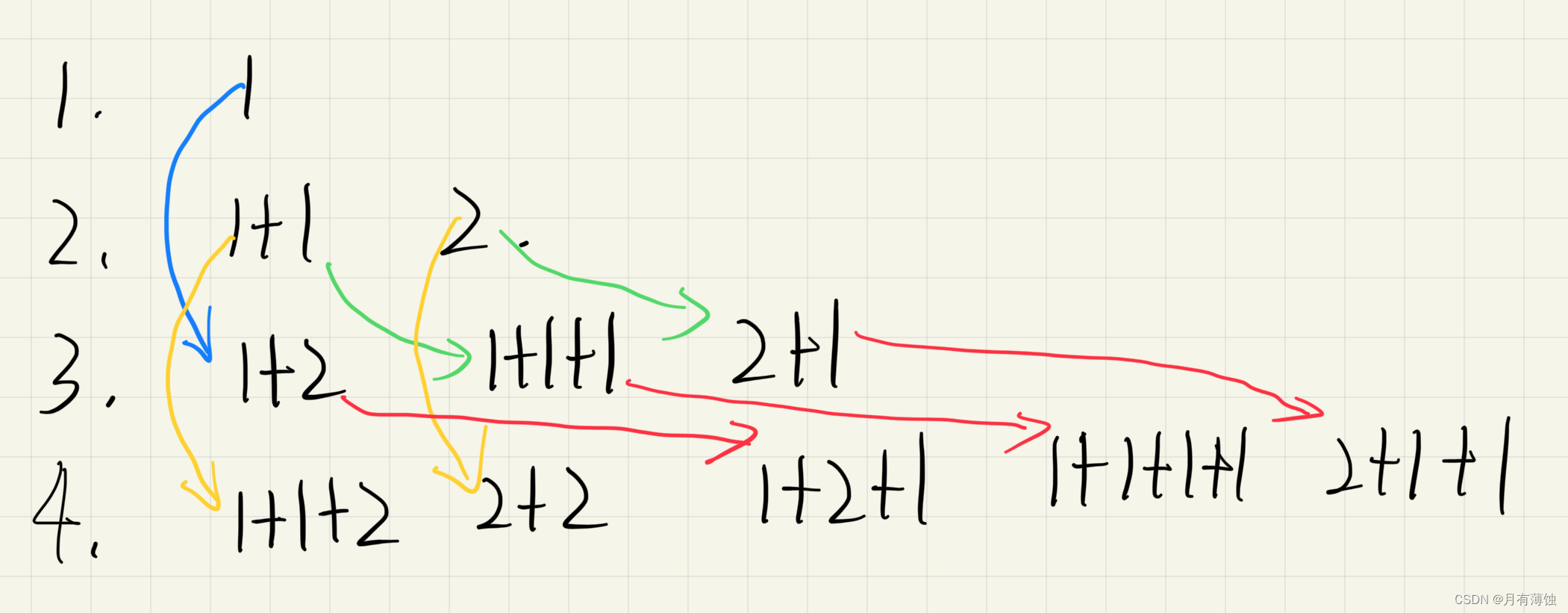
   从第三层开始，第n层需要的步伐等于第n-1层需要的步伐加上第n-2层需要的步伐
   例如：第三层=（第一层+2）+ （第二层+1）
   第四层=（第二层+2） + （第三层+1）
3. dp数组如何初始化
   不考虑dp[0]如何初始化，只初始化dp[1] = 1，dp[2] = 2，然后从i = 3开始递推，这样才符合
   dp[i]的定义。
4. 确定遍历顺序
   从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出，遍历顺序⼀定是从前向后遍历的
5. 举例推导dp数组
   举例当n为5的时候，dp table（dp数组）应该是这样的
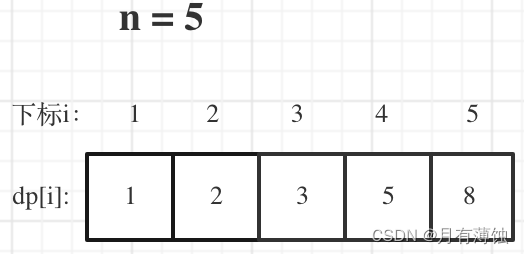   如果代码出问题了，就把dp table 打印出来，看看究竟是不是和⾃⼰推导的⼀样。
   此时⼤家应该发现了，这不就是斐波那契数列么！
   唯⼀的区别是，没有讨论dp[0]应该是什么，因为dp[0]在本题没有意义！

代码

力扣提交代码

class Solution {
public:
	int climbStairs(int n) {
		if (n <= 1) return n; // 因为下⾯直接对dp[2]操作了，防⽌空指针
		vector<int> dp(n + 1);
		dp[1] = 1;
		dp[2] = 2;
		for (int i = 3; i <= n; i++) { // 注意i是从3开始的
			dp[i] = dp[i - 1] + dp[i - 2];
		}
		return dp[n];
	}
};

总代码

#include<bits/stdc++.h>
using namespace std;

int climbStairs(int n) 
{
    if(n<=2)
    	return n;
    int dp[50]={0};
    dp[1]=1;
    dp[2]=2;
    int i;
    for(i=3;i<=n;i++)
    	dp[i]=dp[i-1]+dp[i-2];
    return dp[n];
}

int main()
{
	int n;
	scanf("n = %d",&n);
	cout<<climbStairs(n);
	return 0;
}