【MATLAB】RLMD分解+FFT+HHT组合算法
有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~
1 基本定义
RLMD分解+FFT+HHT组合算法是一种强大的分析方法,结合了局部均值分解(LMD)、快速傅里叶变换(FFT)和希尔伯特-黄变换(HHT)。
首先,使用LMD将原始信号分解成多个IMF(本征模态函数),然后对每个IMF进行FFT计算其频谱,最后使用HHT分析其时频特征。
这种组合方法可以综合利用三种方法的优点,对于处理非线性和非平稳信号具有较高的准确性和鲁棒性。其中,LMD是一种用于处理非线性和非平稳信号的自适应信号分解方法,通过在信号中加入白噪声,并多次进行经验模态分解,从而获得原信号的多种本征模态函数。这些IMF可以更好地捕捉到信号中的局部特征,特别是对于非线性、非平稳信号。FFT是一种高效的计算离散傅里叶变换(DFT)和其逆变换的算法,可以在短时间内计算出信号在频域上的表达,从而提供信号的频率特征。HHT是一种用于分析非线性和非平稳信号的数学工具,通过将信号分解成一系列固有模态函数(IMF),并计算每个IMF的瞬时频率,从而提供信号的时频特征。
这种组合方法在处理复杂的非线性、非平稳信号时具有独特的优势。首先,LMD能够自适应地将信号分解成多个本征模态函数,这些IMF可以更好地捕捉到信号中的局部特征,特别是对于非线性、非平稳信号。其次,FFT可以计算出每个IMF的频谱,提供信号的频率特征,这对于分析信号的周期性和频域特征非常重要。最后,HHT可以提供信号的时频特征,对于分析信号的瞬时频率和时变特性非常有用。
这种组合方法在许多领域都有广泛的应用,例如在机械故障诊断中,可以使用LMD将机器的振动信号分解成多个IMF,然后使用FFT计算每个IMF的频谱,最后使用HHT分析其时频特征,从而识别出机器的故障。此外,在语音信号处理、雷达信号处理、图像处理等领域也可以使用这种组合方法进行分析。
需要注意的是,这种组合方法也存在一些局限性。例如,LMD 和 HHT 都存在端点效应问题,即在进行信号分解和分析时,需要考虑信号的边界条件。此外,这种组合方法需要使用大量的计算资源,特别是在处理大规模数据时,需要进行多次 FFT 和 HHT 计算。因此,在实际应用中需要根据具体的问题和数据特点进行选择和优化。
此外,这种组合方法还具有很高的鲁棒性,即使在信号存在噪声或异常值的情况下,也能够提供相对准确的结果。这是因为它可以自适应地处理非线性、非平稳信号,并且通过FFT和HHT提供更全面的频率和时频特征,从而减少噪声和异常值对结果的影响。
在具体实现上,这种组合方法需要使用相关的数学库和工具软件,例如Python中的NumPy、SciPy和Matlab中的信号处理工具箱等。这些库和工具软件提供了各种函数和算法,可以方便地实现LMD、FFT和HHT等算法,并且提供了可视化界面和文档支持,方便用户进行学习和应用。
总之,RLMD分解+FFT+HHT组合算法是一种非常强大的分析方法,可以用于处理非线性和非平稳信号,提供全面的频率和时频特征,并且具有较高的准确性和鲁棒性。它在许多领域都有广泛的应用前景,需要根据具体的问题和数据特点进行选择和优化。
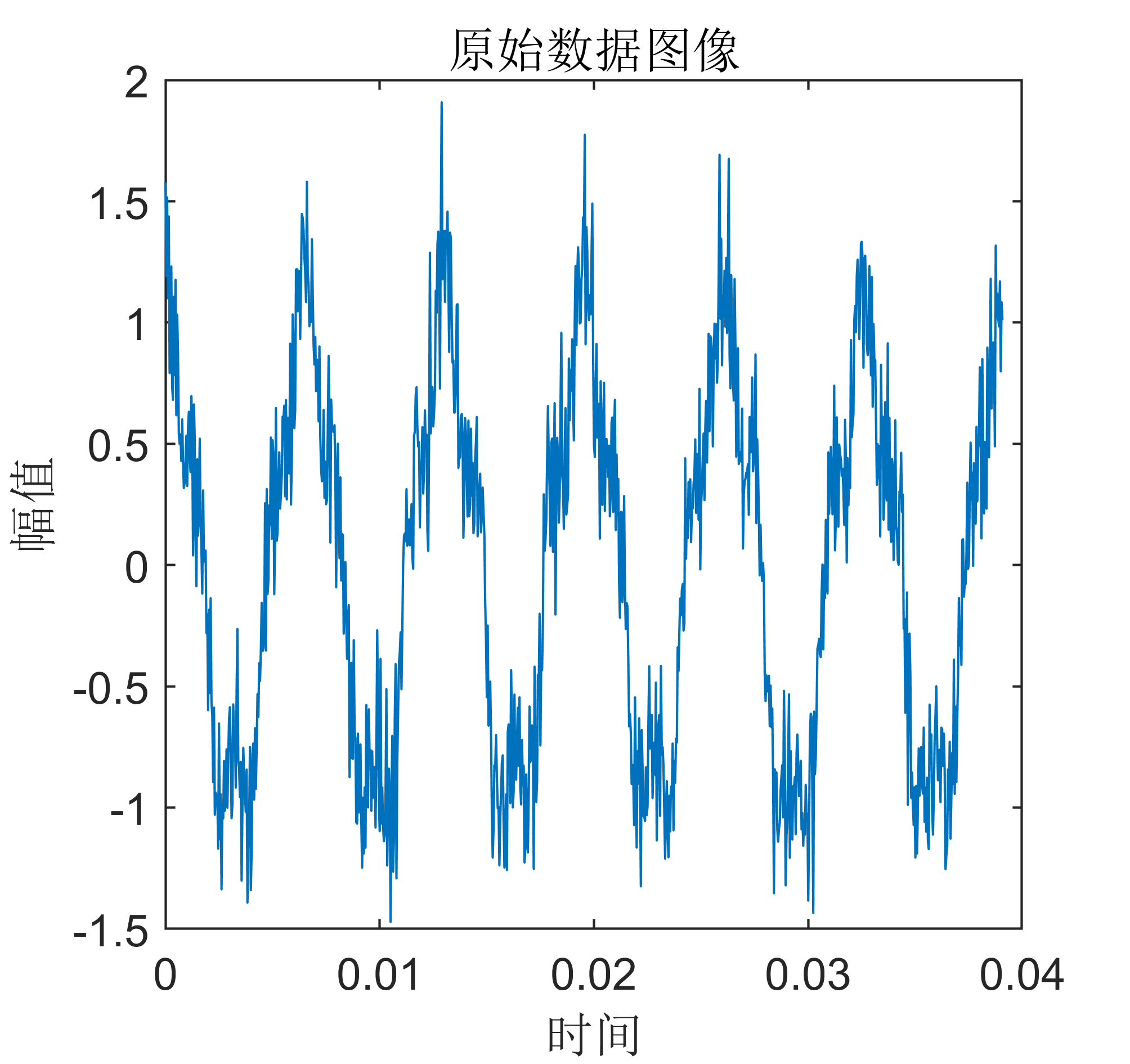
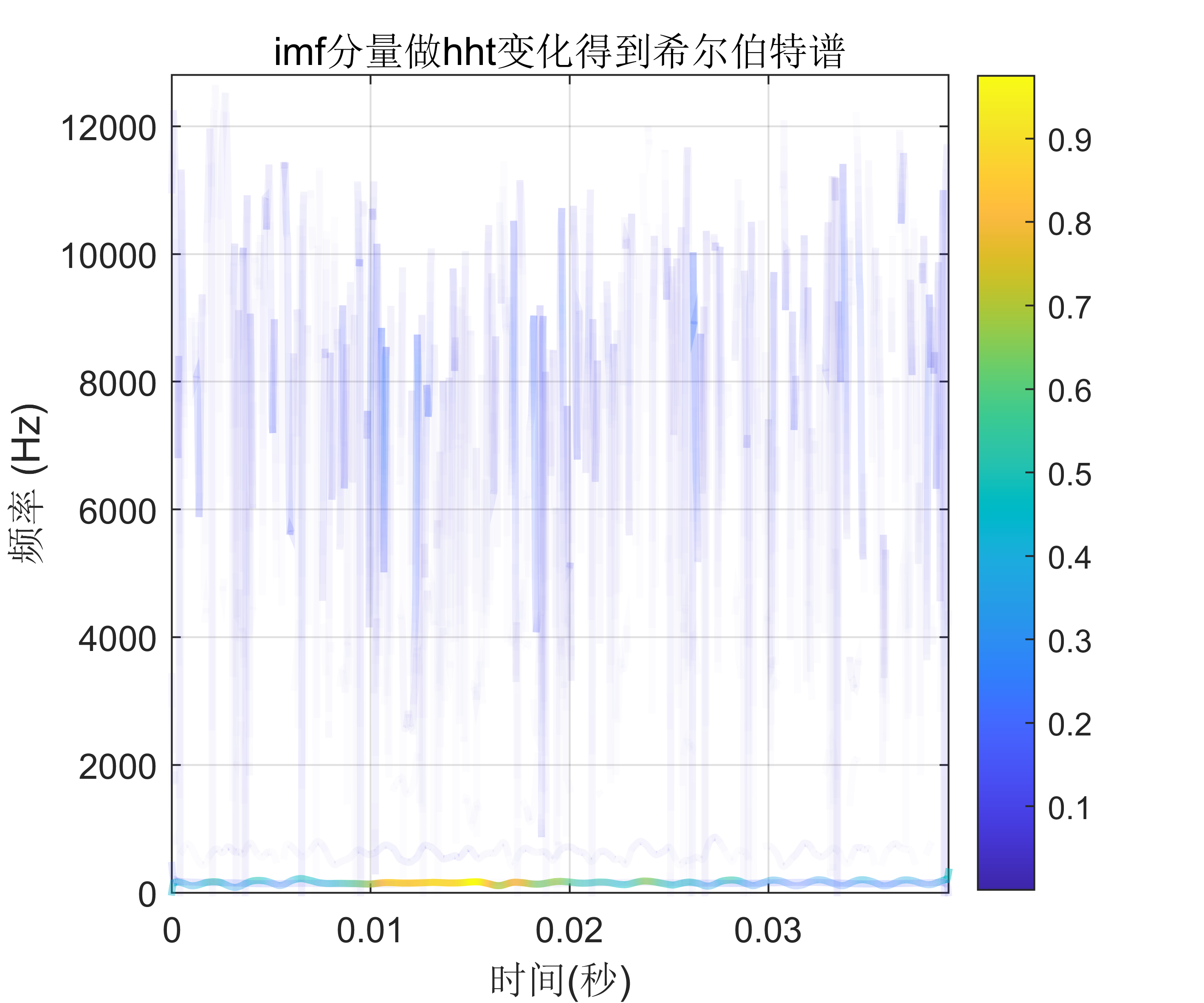
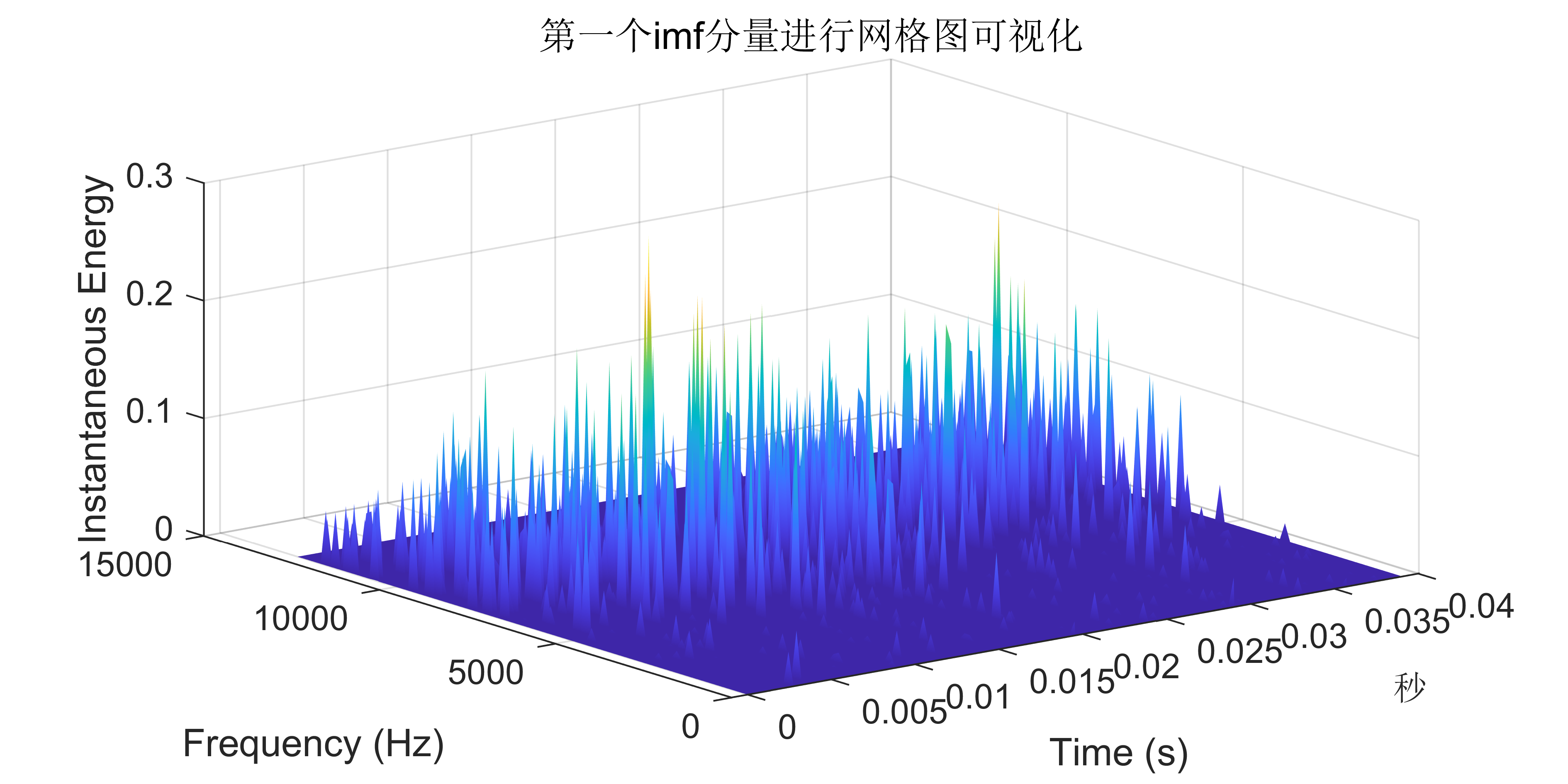
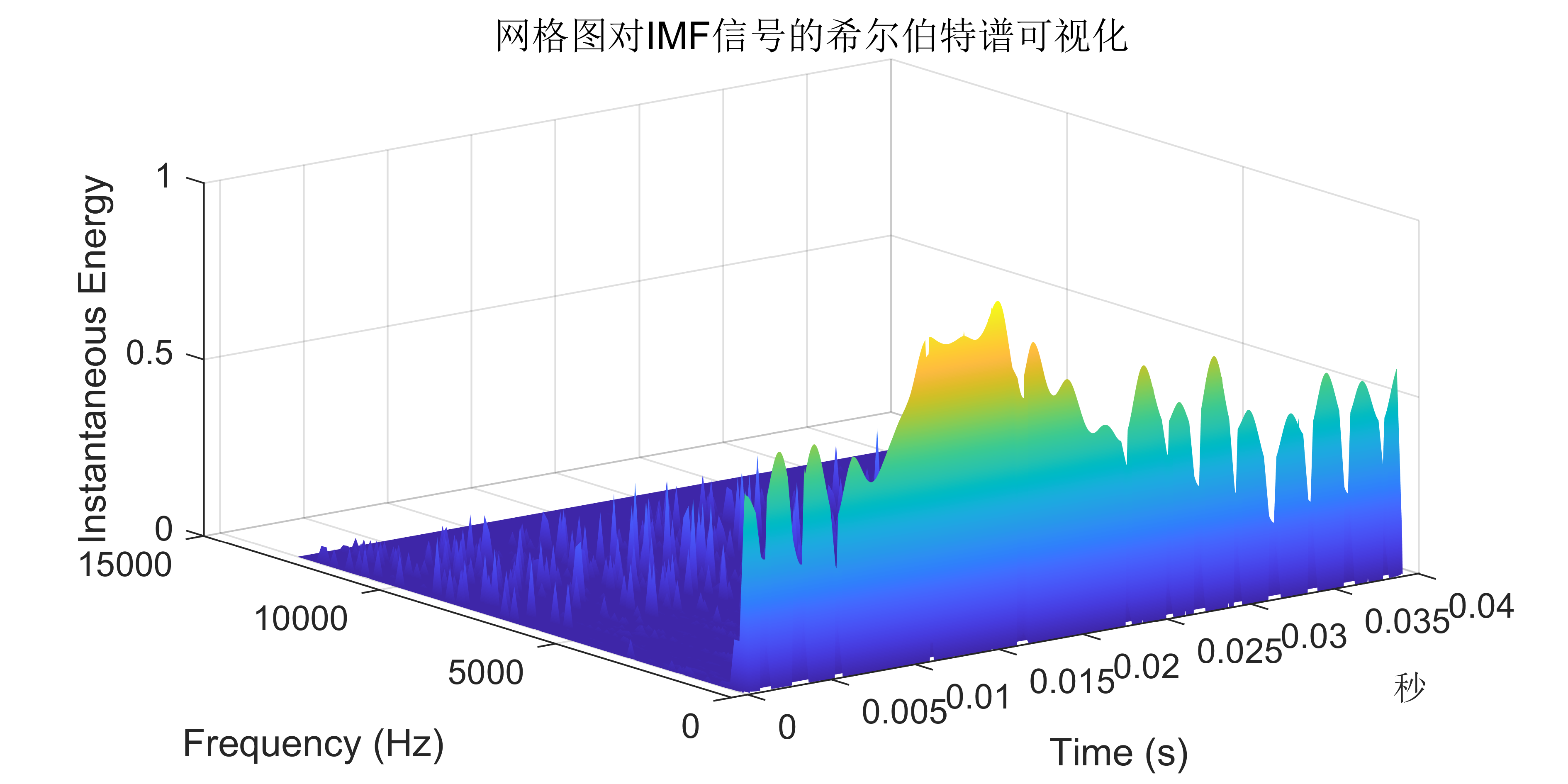
2 出图效果
附出图效果如下:


附视频教程操作:
