优化器原理——权重衰减(weight_decay)
优化器原理——权重衰减(weight_decay)
- weight_decay的作用
- 原理解析
- 实验观察
在深度学习中,优化器的
weight_decay 参数扮演着至关重要的角色。它主要用于实现正则化,以防止模型过拟合。过拟合是指模型在训练数据上表现优异,但在新的、未见过的数据上却表现不佳。这通常是因为模型学习了训练数据中的噪声和细节,而不是数据背后的真实模式。
weight_decay的作用
防止过拟合:weight_decay 通过对模型的大权重施加惩罚,促使模型保持简洁,从而降低了学习训练数据噪声的可能性,提高了模型在新数据上的泛化能力。
促进稀疏解:此外,正则化倾向于将权重推向零,这有助于在某些场景下获得更为简洁和稀疏的模型。
原理解析
从数学的角度来看,weight_decay 实际上是 L2 正则化的一种表现形式。L2 正则化在原始损失函数的基础上增加了一个与权重平方成正比的项,修改后的损失函数表示为:
L = L o r i g i n a l + λ 2 ∑ w 2 L = L_{original} + \frac{\lambda}{2} \sum w^2 L=Loriginal+2λ∑w2
其中:
·
L
o
r
i
g
i
n
a
l
L_{original}
Loriginal 是原始的损失函数。
·
λ
\lambda
λ 是正则化参数,对应于 weight_decay。
·
∑
w
2
\sum w^2
∑w2 表示权重的平方和。
正则化参数
λ
\lambda
λ 的大小决定了对大权重的惩罚程度。较高的 weight_decay 值增强了对复杂模型结构的惩罚,有助于防止过拟合。但是,如果设置过高,可能会导致模型欠拟合,失去捕捉数据中重要特征的能力。
在训练期间,优化器不仅要最小化原始的损失函数,还要考虑权重的惩罚项,这样做有助于在拟合训练数据和保持模型的简单性之间找到一个平衡点。因此,weight_decay 是优化模型在看不见的数据上表现的一个重要手段。
实验观察
为了直观地理解 weight_decay 的影响,我们可以进行一个简单的实验,比较不同 weight_decay 值对训练过程的影响。例如,我们可以对比 weight_decay = 0.01 与 weight_decay = 0.1 的效果,具体代码如下:
import torch
from tensorboardX import SummaryWriter
from torch import optim, nn
import time
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.linears = nn.Sequential(
nn.Linear(2, 20),
nn.LayerNorm(20),
nn.Linear(20, 20),
nn.LayerNorm(20),
nn.Linear(20, 20),
nn.LayerNorm(20),
nn.Linear(20, 20),
nn.LayerNorm(20),
nn.Linear(20, 1),
)
def forward(self, x):
_ = self.linears(x)
return _
lr = 0.01
iteration = 1000
x1 = torch.arange(-10, 10).float()
x2 = torch.arange(0, 20).float()
x = torch.cat((x1.unsqueeze(1), x2.unsqueeze(1)), dim=1)
y = 2*x1 - x2**2 + 1
model = Model()
optimizer = optim.Adam(model.parameters(), lr=lr, weight_decay=0.1)
loss_function = torch.nn.MSELoss()
start_time = time.time()
writer = SummaryWriter(comment='_权重衰减')
for iter in range(iteration):
y_pred = model(x)
loss = loss_function(y, y_pred.squeeze())
loss.backward()
for name, layer in model.named_parameters():
writer.add_histogram(name + '_grad', layer.grad, iter)
writer.add_histogram(name + '_data', layer, iter)
writer.add_scalar('loss', loss, iter)
optimizer.step()
optimizer.zero_grad()
if iter % 50 == 0:
print("iter: ", iter)
print("Time: ", time.time() - start_time)
这里我们使用 TensorBoardX 进行结果的可视化展示。
通过观察训练1000轮后线性层的梯度分布,我们可以看出,较大的 weight_decay 设置会导致模型的权重更倾向于靠近 0。这说明 weight_decay 值越大,优化器在限制权重增长上越严格。
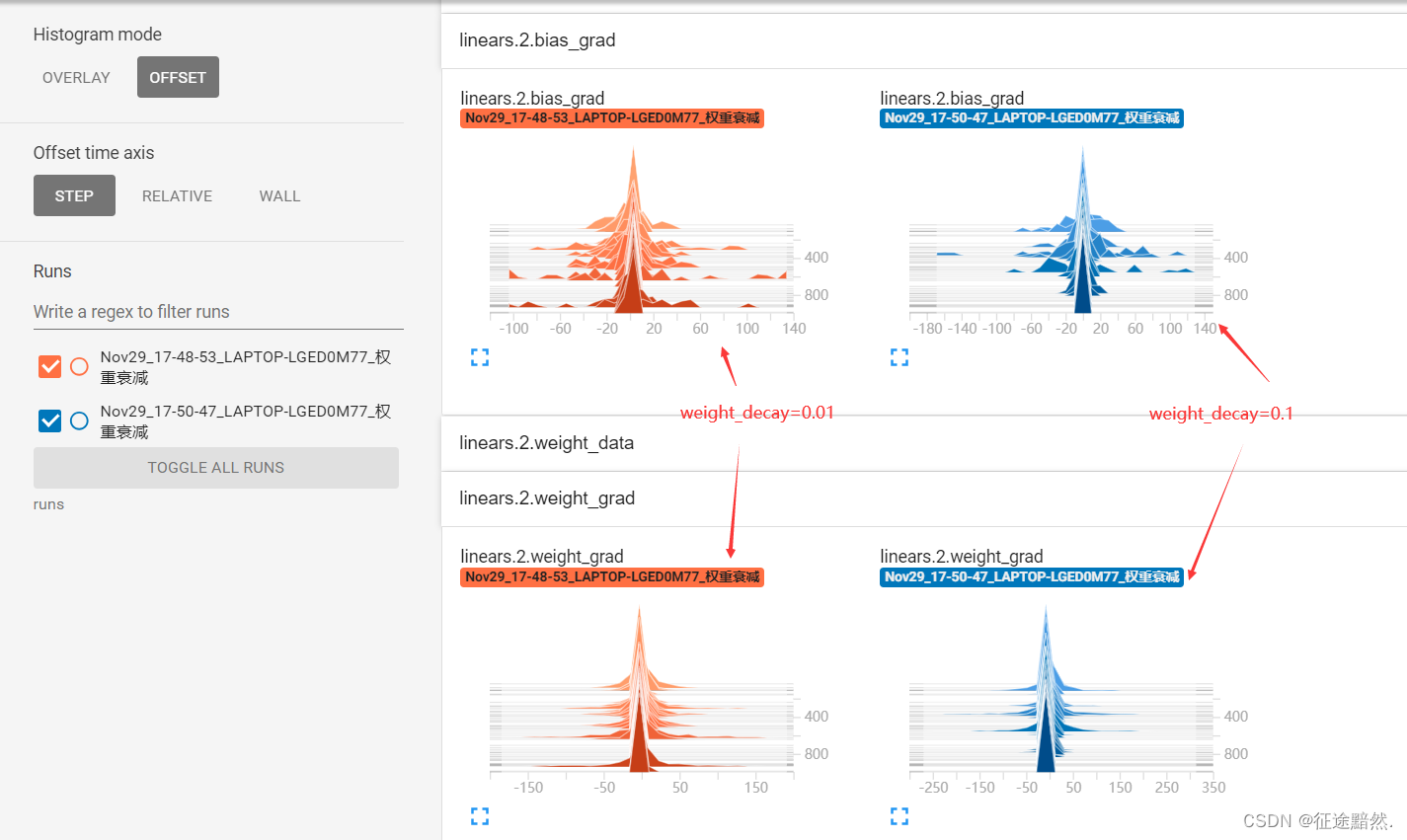
可以看到,weight_decay设置的较大,会限制模型的权重分布都会趋近于0。可以理解为weight_decay越大,优化器就越限制权重分布变得趋近 0。
