#D. 竞选班长
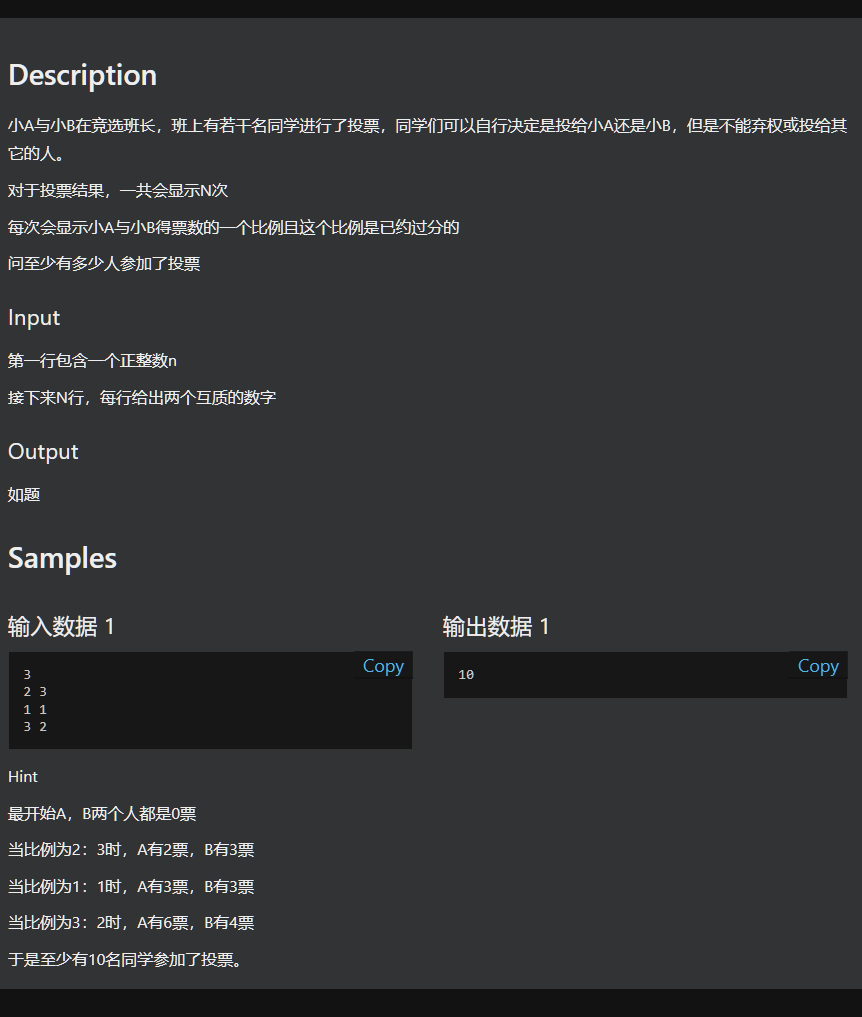
题目
思路1
可以发现题目问的是
至少有多少人参加了投票
并且题目中有一句
不能弃权或投给其它的人
所以A和B的票数如果从前往后看的话,那么按理来说应该是不递减的(后面一次票数>=前面一次的票数)
可是比例是已约过分的
所以可能不递减
那么我们可以不断将A的票数和B的票数一起*i(i不断+1)
直到A,B的票数都>=AB上一次的票数
最后输出A,B最终的票数和就行了
程序1
#include <bits/stdc++.h>
#define ll long long
using namespace std;
int n,a[10000001],b[10000001];
signed main()
{
cin>>n;
for(int i = 1;i <= n;i++) cin>>a[i]>>b[i];
for(int i = 2;i <= n;i++)
{
int t = a[i],t_2 = b[i];
while(a[i] < a[i - 1] || b[i] < b[i - 1])
a[i] += t,b[i] += t_2;
}
cout<<a[n] + b[n];
return 0;
}但是,提交上去后,37分,TLE了。。。
思路2
我们可以发现TLE的原因是
int t = a[i],t_2 = b[i];
while(a[i] < a[i - 1] || b[i] < b[i - 1])
a[i] += t,b[i] += t_2;这段代码要一个个去倍增,那么怎么优化呢?
我们每次处理A,B的票数时可以分3种情况
a[i] < a[i - 1] && b[i] >= b[i - 1]
这样,a[i]不符合条件,但是b[i]符合,所以我们用t记录下a[i - 1]/a[i]并向上取整的结果
a[i] >= a[i - 1] && b[i] < b[i - 1]
这样,b[i]不符合条件,但是a[i]符合,所以我们用t记录下b[i - 1]/b[i]并向上取整的结果
a[i] < a[i - 1] && b[i] < b[i - 1]
这样,a[i]不符合条件,b[i]也符合,所以我们用t记录下max(a[i - 1]/a[i],b[i - 1 / b[i]])并都向上取整的结果
最后将a[i],b[i] * t就行了。
向上取整的原因:如果向下取整,举个例子a[i - 1]=6,a[i] = 4,那么6/4向下取整是1,可是4*1不>=6,只能*2,所以只能向上取整。
AC代码
#include <bits/stdc++.h>
#define int long long
using namespace std;
int n,a[10000001],b[10000001],ta[10000001],tb[10000001],t;
int f(int x,int y)//返回x/y的向上取整的结果
{
if(x % y != 0) return x / y + 1;
else return x / y;
}
signed main()
{
scanf("%lld",&n);
for(int i = 1; i <= n; i++)
{
scanf("%lld%lld",&a[i],&b[i]);
if(i > 1 && ((a[i] < a[i - 1])||(b[i] < b[i - 1])))//只要a[i]/b[i]有一个不符合条件
{
if(a[i] < a[i - 1] && b[i] >= b[i - 1]) t = f(a[i - 1],a[i]);
else if(a[i] >= a[i - 1] && b[i] < b[i - 1]) t = f(b[i - 1],b[i]);
else if(a[i] < a[i - 1] && b[i] < b[i - 1])
{
int tt = f(a[i - 1],a[i]),ttt = f(b[i - 1],b[i]);
t = max(ttt,tt);
}
a[i] *= t;
b[i] *= t;
}
}
printf("%lld",a[n] + b[n]);
return 0;
}