【数值计算方法(黄明游)】矩阵特征值与特征向量的计算(五):Householder方法【理论到程序】
文章目录
矩阵的特征值(eigenvalue)和特征向量(eigenvector)在很多应用中都具有重要的数学和物理意义。Householder 矩阵和变换提供了一种有效的方式,通过反射变换将一个向量映射到一个标准的方向,这对于一些数值计算问题具有重要的意义。
本文将详细介绍Householder方法的基本原理和步骤,并给出其Python实现。
一、Jacobi 旋转法
Jacobi 旋转法的每一次迭代中,需要选择一个非对角元素最大的位置,然后构造相应的旋转矩阵,进行相似变换,使得矩阵逐渐对角化。
二、Jacobi 过关法
Jacobi 过关法(Jacobi’s threshold method)是 Jacobi 旋转法的一种改进版本,其主要目的是减少计算工作和提高运行速度。该方法通过动态调整阈值,并根据阈值对非对角元素进行选择性的旋转变换,以逐步对角化对称矩阵。
三、Householder 方法
如果对任意向量 z z z,我们可以将其分解为与 u u u 平行的分量 a u au au 和与 u u u 正交的分量 b v bv bv,即 z = a u + b v z = au + bv z=au+bv,那么 Householder 变换会将 z z z 变换为 − a u + b v -au + bv −au+bv。这个变换可以理解为镜面反射,它不改变向量在与 u u u 正交的平面上的投影,但将向量沿着 u u u 的方向反射。数学表达式为:
H z = a u + b v → − a u + b v Hz = au + bv \rightarrow -au + bv Hz=au+bv→−au+bv
这个性质使得 Householder 变换在一些数值计算的应用中非常有用,例如 QR 分解等。
1. 旋转变换
在 Householder 方法中,通过一系列的正交相似变换,可以将实对称矩阵 (A) 转化为三对角矩阵。不同于 Jacobi 旋转法( a i j = a j i = 0 a_{ij}= a_{ji}=0 aij=aji=0),Householder 方法的旋转矩阵选择的角度使得 c i k = c k j = 0 c_{ik}= c_{kj}=0 cik=ckj=0。
a. 旋转变换的选择
对于实对称矩阵
A
A
A 中的元素
a
i
k
a_{ik}
aik ,选择适当的旋转角度
θ
\theta
θ ,可以使得
a
i
k
a_{ik}
aik 变为零。具体而言,选择
θ
\theta
θ 使得:
c
i
k
=
c
k
j
=
a
i
k
cos
(
θ
)
+
a
j
k
sin
(
θ
)
=
0
c_{ik}= c_{kj}=a_{ik} \cos(\theta) + a_{jk} \sin(\theta) = 0
cik=ckj=aikcos(θ)+ajksin(θ)=0
通过这样的选择,我们可以构造一个旋转矩阵 P i , j , k P_{i,j,k} Pi,j,k,该矩阵对应的正交相似变换可以将 c i k c_{ik} cik 变为零。这一过程实现了对实对称矩阵的正交相似变换,使得某些元素变为零,逐步实现了将矩阵转化为三对角形式。
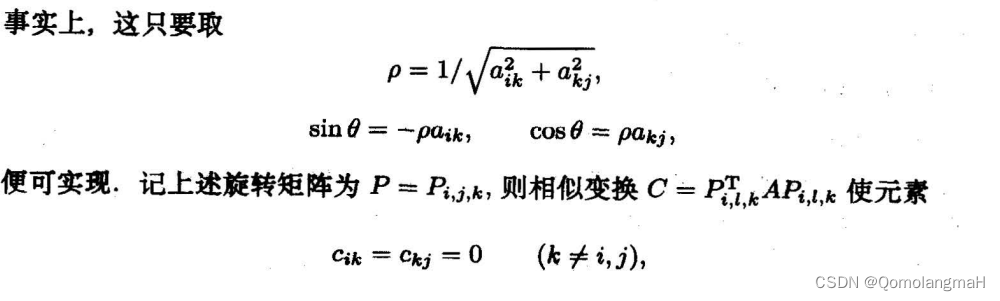
b. 旋转变换的顺序
在进行 Householder 变换时,旋转的顺序很重要。通常,可以选择按列进行变换。例如,对于 i = 2 , … , n − 1 i = 2, \ldots, n-1 i=2,…,n−1,可以依次选择 j = i + 1 , i + 2 , … , n j = i+1, i+2, \ldots, n j=i+1,i+2,…,n,然后对每一对 ( i , j ) (i, j) (i,j) 进行正交相似变换,将 a i k a_{ik} aik 变为零。整个过程的迭代将会逐步将实对称矩阵 A A A 转化为三对角矩阵 C C C。
2. Householder矩阵(Householder Matrix)
a. H矩阵的定义
设 u u u为单位向量,即 ∥ u ∥ = 1 \|u\| = 1 ∥u∥=1。定义 Householder 矩阵 H = I − 2 u u T H = I - 2uu^T H=I−2uuT,其中 I I I 为单位矩阵。这个矩阵具有以下性质:
- 对称性: H T = H H^T = H HT=H,即 Householder 矩阵是对称的。
- 正交性: H T H = I H^T H = I HTH=I,即 Householder 矩阵是正交矩阵。
- 保范性: 对于任意非零向量
x
x
x 和
y
y
y,如果
∥
x
∥
2
=
∥
y
∥
2
\|x\|^2 = \|y\|^2
∥x∥2=∥y∥2,则存在 Householder 矩阵
H
H
H,使得
H
x
=
y
Hx = y
Hx=y。
- 考虑 Householder 矩阵对向量 u u u 的作用: H u = ( I − 2 u u T ) u = − u Hu = (I - 2uu^T)u = -u Hu=(I−2uuT)u=−u。这说明 Householder 矩阵将向量 u u u 反射到其负向量上。
- 对于任何与 u u u 正交的向量 v v v,有 H v = ( I − 2 u u T ) v = v Hv = (I - 2uu^T)v = v Hv=(I−2uuT)v=v,即 Householder 矩阵保持与 u u u 正交的向量不变。
- 因此对任意向量
z
z
z,设
z
=
a
u
+
b
v
z = au + bv
z=au+bv,那么 Householder 变换会将
z
z
z 变换为
−
a
u
+
b
v
-au + bv
−au+bv,数学表达式为:
H z = a ( H u ) + b ( H v ) → − a u + b v Hz = a(Hu) + b(Hv) \rightarrow -au + bv Hz=a(Hu)+b(Hv)→−au+bv
b. H变换的几何解释
可以将 Householder 变换视为镜面反射。考虑 u u u 为反射面上的单位法向量。对于任意 z z z,Householder 变换将 z z z 的投影反射到 − u -u −u方向,同时保持投影在反射面上。
c. H变换的应用场景
- 矩阵三对角化: 在计算线性代数中,Householder 变换常用于将矩阵化为三对角形式,以便更容易进行特征值计算等操作。
- QR 分解: Householder 变换是计算 QR 分解的基本工具,用于将矩阵分解为一个正交矩阵和一个上三角矩阵的乘积。
3. H变换过程详解
a. 过程介绍
对于矩阵
A
A
A 的某一列向量
a
=
(
a
1
,
a
2
,
…
,
a
n
)
T
\mathbf{a} = (a_1, a_2, \ldots, a_n)^T
a=(a1,a2,…,an)T,如果我们想将向量的后
n
−
(
r
+
1
)
n - (r+1)
n−(r+1)个分量化为零,即将
a
\mathbf{a}
a 变为
c
=
(
a
1
,
a
2
,
…
,
a
r
,
−
sign
(
a
r
+
1
)
s
,
0
,
…
,
0
)
T
\mathbf{c} = (a_1, a_2, \ldots, a_r, -\text{sign}(a_{r+1})s, 0, \ldots, 0)^T
c=(a1,a2,…,ar,−sign(ar+1)s,0,…,0)T,其中
s
=
∥
a
∥
2
s = \|a\|_2
s=∥a∥2 (从
r
+
1
r+1
r+1计算到
n
n
n)且
a
r
+
1
≠
0
a_{r+1} \neq 0
ar+1=0,则可以引入 Householder 矩阵
H
H
H,使得
H
a
=
c
Ha=c
Ha=c。Householder 矩阵的计算方式如下:
w
=
a
−
sign
(
a
r
+
1
)
s
e
r
+
1
\mathbf{w} = \mathbf{a} - \text{sign}(a_{r+1})s\mathbf{e}_{r+1}
w=a−sign(ar+1)ser+1
其中,
e
r
+
1
\mathbf{e}_{r+1}
er+1 是单位向量
(
0
,
0
,
…
,
0
,
1
,
0
,
…
,
0
)
T
(0, 0, \ldots, 0, 1, 0, \ldots, 0)^T
(0,0,…,0,1,0,…,0)T,具体位置在第
r
+
1
r+1
r+1 个。

b. 细节解析
- Householder 矩阵的构造:
- 通过 Householder 变换,构造 Householder 矩阵 H H H,将某一列 a j a_j aj的 r + 1 r+1 r+1 到 n n n 个分量化为零。
-
计算过程的稳定性:
- 将 a a a 的 r + 1 r+1 r+1 到 n n n 个分量的符号设定为 − sign ( a r + 1 ) -\text{sign}(a_{r+1}) −sign(ar+1),以增强计算的稳定性。
-
计算相似三对角矩阵:
- 将 A A A 逐列进行正交相似变换,得到 A 1 , A 2 , … , A n − 1 A_1, A_2, \ldots, A_{n-1} A1,A2,…,An−1。
- 最终得到相似三对角矩阵 G = A n = H n − 2 ⋅ … ⋅ H 2 ⋅ H 1 ⋅ A G = A_n = H_{n-2} \cdot \ldots \cdot H_2 \cdot H_1 \cdot A G=An=Hn−2⋅…⋅H2⋅H1⋅A。
-
实际计算中的优化:
- 实际计算中,无需形成所有的 Householder 矩阵,也无需进行矩阵乘法运算,可以直接在原矩阵上进行计算。

- 实际计算中,无需形成所有的 Householder 矩阵,也无需进行矩阵乘法运算,可以直接在原矩阵上进行计算。
4. H变换例题解析
给定矩阵:
A
=
[
1
2
1
2
2
2
−
1
1
1
−
1
1
1
2
1
1
1
]
A = \begin{bmatrix} 1 & 2 & 1 & 2 \\ 2 & 2 & -1 & 1 \\ 1 & -1 & 1 & 1 \\ 2 & 1 & 1 & 1 \end{bmatrix}
A=
121222−111−1112111

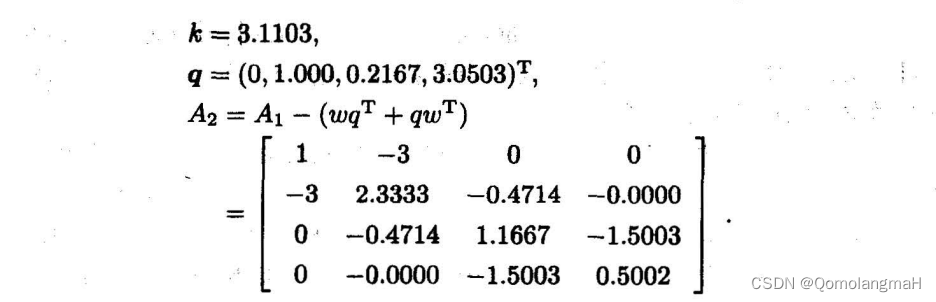
最终的三对角矩阵 A 2 A_2 A2:
-
A
2
A_2
A2的形式为
A 2 = [ 1 − 3 0 0 − 3 2.3333 − 0.4714 0 0 − 0.4714 1.1667 − 1.5003 0 0 − 1.5003 0.5002 ] A_2 = \begin{bmatrix} 1 & -3 & 0 & 0 \\ -3 & 2.3333 & -0.4714 & 0 \\ 0 & -0.4714 & 1.1667 & -1.5003 \\ 0 & 0 & -1.5003 & 0.5002 \end{bmatrix} A2= 1−300−32.3333−0.471400−0.47141.1667−1.500300−1.50030.5002
这样,通过选择 r = 1 r=1 r=1 和 r = 2 r=2 r=2 进行两次 Householder 变换,矩阵 A A A 被成功地化为三对角形式 A 2 A_2 A2。
四、Python实现
import numpy as np
def householder_matrix(v):
"""
给定向量 v,返回 Householder 变换矩阵 H
"""
v = np.array(v, dtype=float)
if np.linalg.norm(v) == 0:
raise ValueError("无效的输入向量,它应该是非零的。")
v = v / np.linalg.norm(v)
H = np.eye(len(v)) - 2 * np.outer(v, v)
return H
def householder_reduction(A):
"""
对矩阵 A 执行 Householder 变换,将其化为三对角形式。
"""
m, n = A.shape
if m != n:
raise ValueError("输入矩阵 A 必须是方阵。")
Q = np.eye(m) # 初始化正交矩阵 Q
for k in range(n - 2):
x = A[k + 1:, k]
e1 = np.zeros_like(x)
e1[0] = 1.0
v = np.sign(x[0]) * np.linalg.norm(x) * e1 + x
v = v / np.linalg.norm(v)
H = np.eye(m)
H[k + 1:, k + 1:] -= 2.0 * np.outer(v, v)
Q = np.dot(Q, H)
A = np.dot(H, np.dot(A, H))
return Q, A
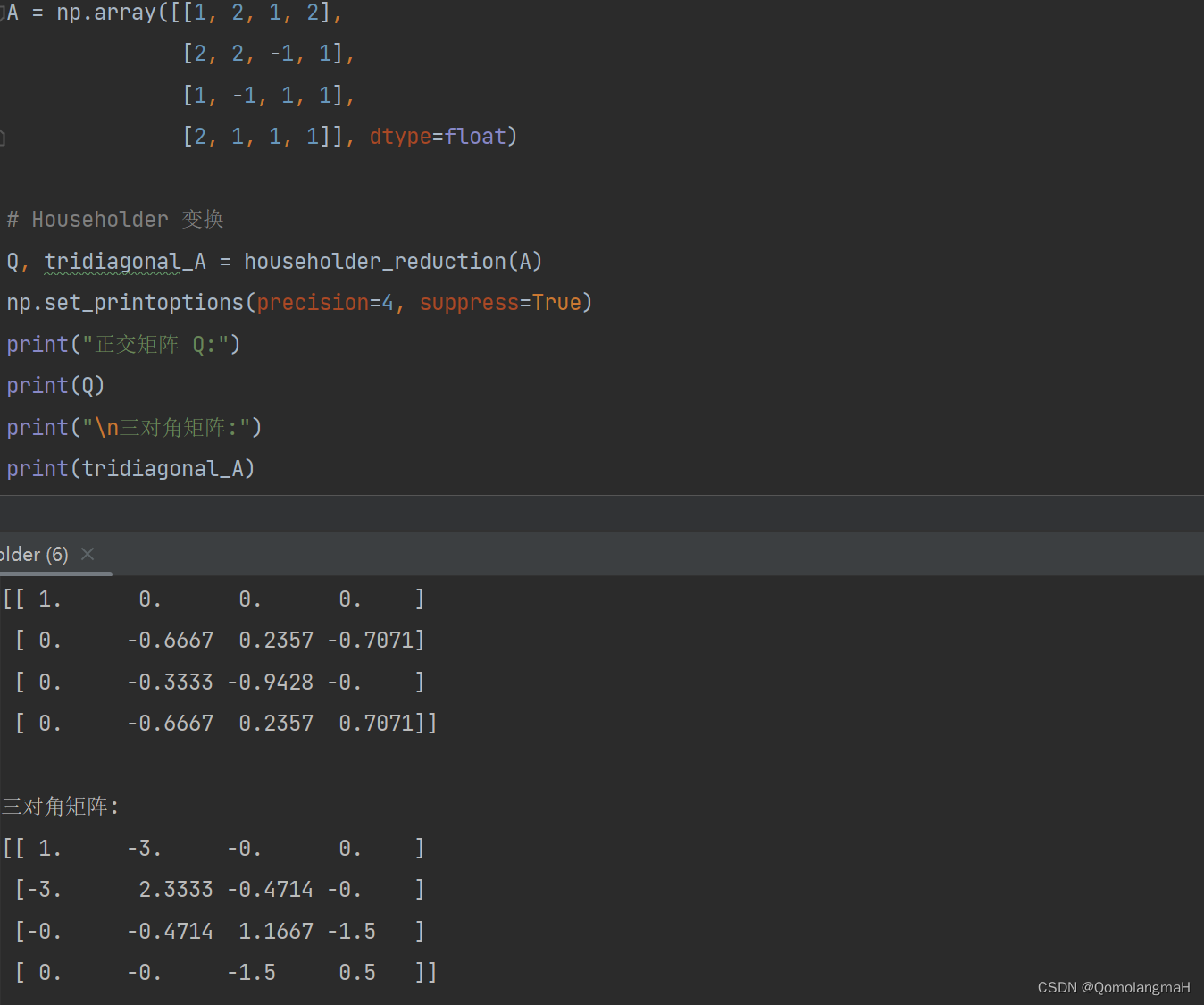
# 示例矩阵
A = np.array([[1, 2, 1, 2],
[2, 2, -1, 1],
[1, -1, 1, 1],
[2, 1, 1, 1]], dtype=float)
# Householder 变换
Q, tridiagonal_A = householder_reduction(A)
np.set_printoptions(precision=4, suppress=True)
print("正交矩阵 Q:")
print(Q)
print("\n三对角矩阵:")
print(tridiagonal_A)

调试过程
-
第一次:
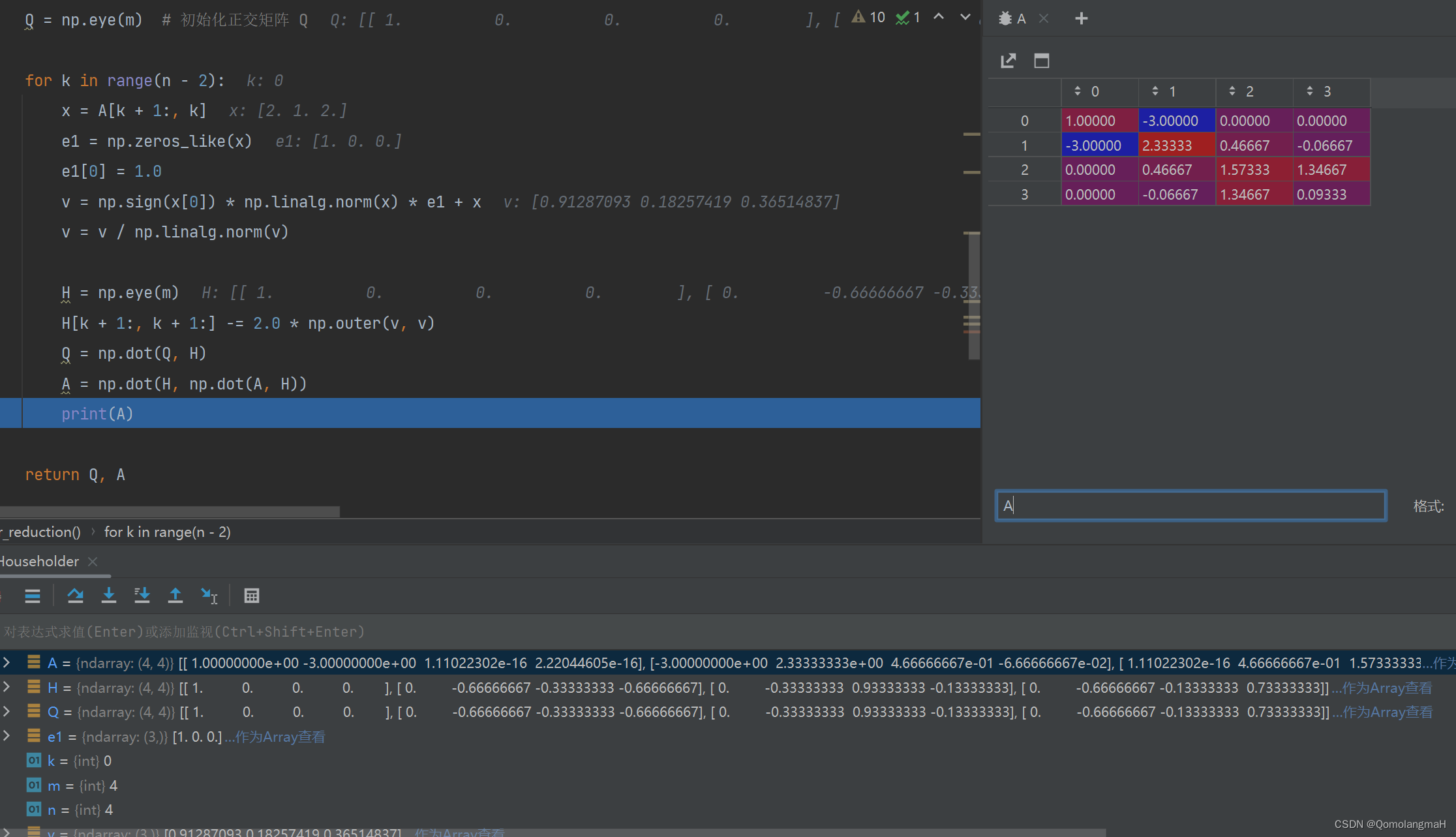
-
第二次:
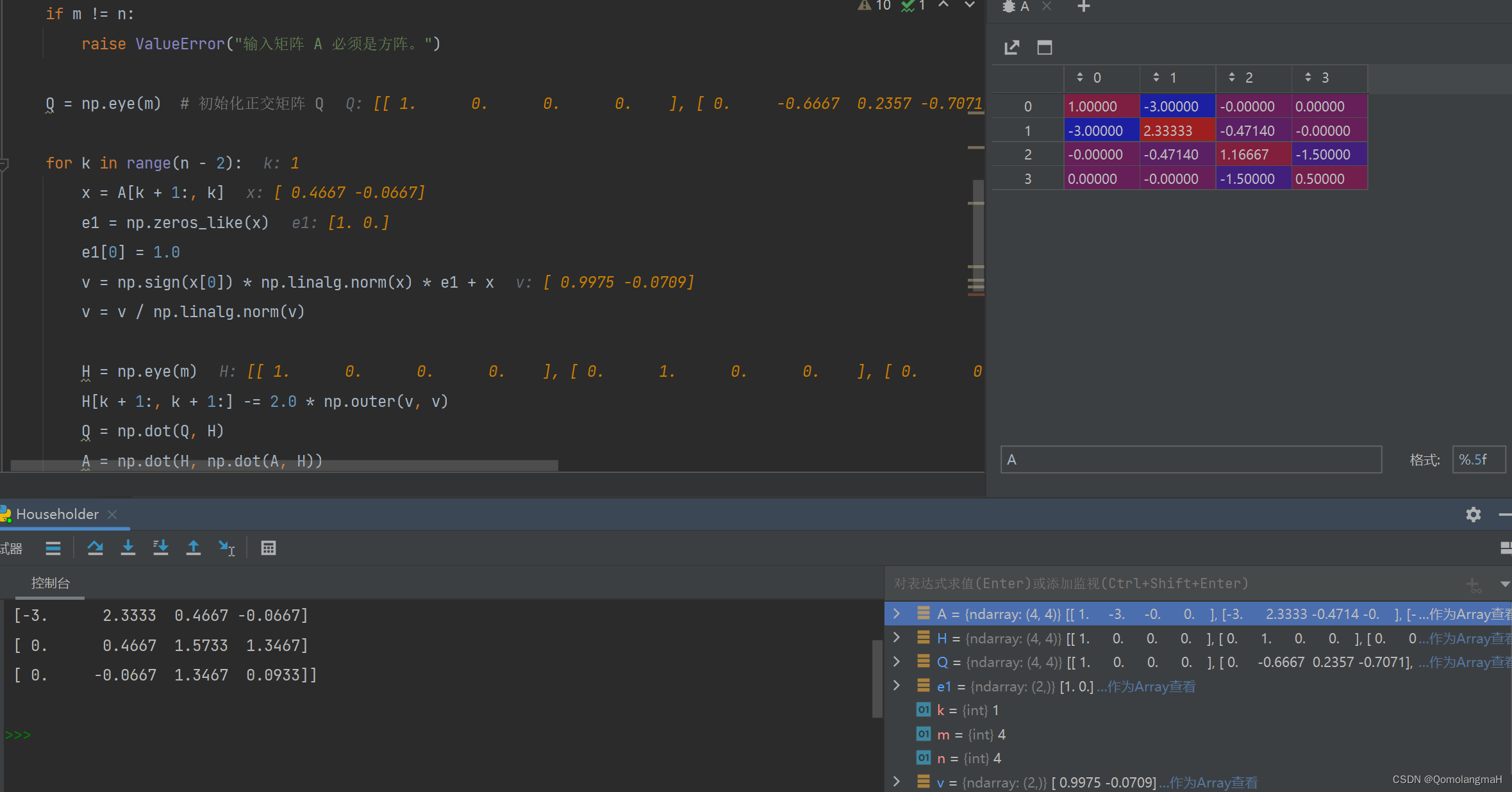
-
final: