12.1 二叉树简单题
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
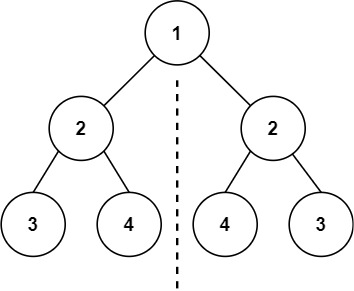
输入:root = [1,2,2,3,4,4,3] 输出:true
思路:对称二叉树 有一个特点是以 中左右顺序遍历左子树的结果会等于 中右左顺序遍历右子树的结果。则用递归的方式
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
bool isEquel(TreeNode* left,TreeNode* right)
{
if(!left && !right) return true;
else if(!left || !right) return false;
if(left->val == right->val)
{
return isEquel(left->left,right->right) && isEquel(left->right,right->left);
}
else
{
return false;
}
}
bool isSymmetric(TreeNode* root) {
//左子树 中左右序 遍历的结果 = 右子树 中右左序 遍历的结果
if(!root||!root->left&&!root->right) return true;
if(!root->left || !root->right) return false;
return isEquel(root->left,root->right);
}
};- 时间复杂度:这里遍历了这棵树,渐进时间复杂度为 O(n)。
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
示例 1:
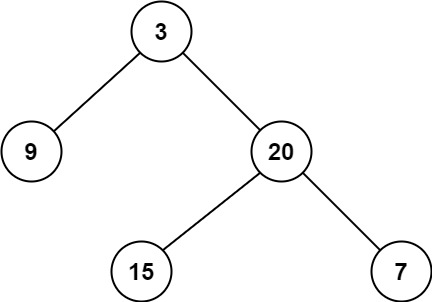
输入:root = [3,9,20,null,null,15,7] 输出:2
思路:题目中是要求找 到叶子节点(左 右子节点为nullptr)的最小深度,并不是空节点的最小深度。
可以用深度优先遍历该树,每次到叶子节点则进行最小值的迭代判断。
细节:引入记录当前深度和最小值的 变量
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void findMinDepth(TreeNode* root,int& depth,int& cur)
{
if(!root) return;
else if(!root->left && !root->right)
{
depth=min(depth,cur+1);
}
cur++;
findMinDepth(root->left,depth,cur);
findMinDepth(root->right,depth,cur);
cur--;
return;
}
int minDepth(TreeNode* root)
{
if(root)
{
int depth=INT_MAX;
int cur=0;
findMinDepth(root,depth,cur);
return depth;
}
else return 0;
}
};-
时间复杂度:O(N),其中 N是树的节点数。对每个节点访问一次。
