深度学习 -- 卷积神经网络
1、卷积神经网络的结构
大卫·休伯尔( David Hunter Hubel ) 等人研究发现,猫的视皮层上 存在简单细胞( simple cell )和复杂细胞( complex cell ),简单细胞会对 感受野中特定朝向的线段做出反应,而复杂细胞对于特定朝向的钱段移动也能做出反应,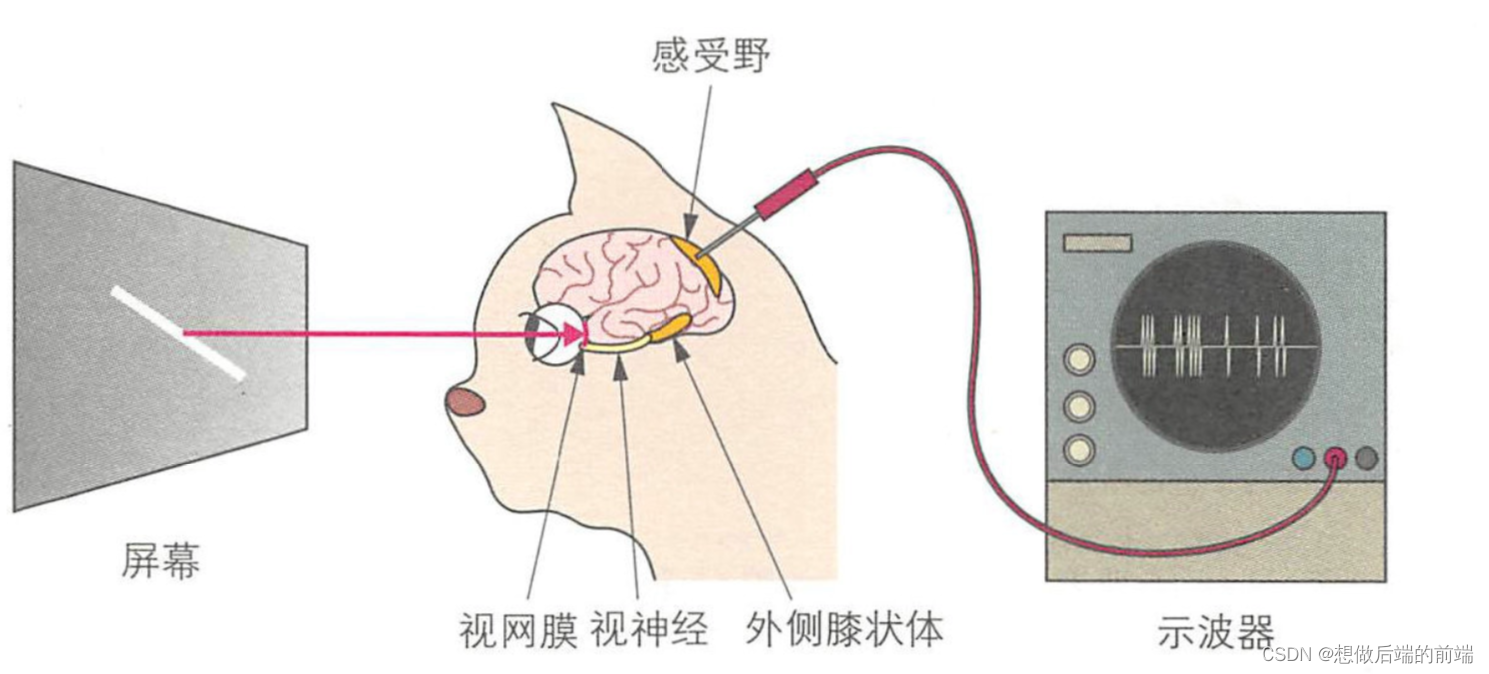
福岛邦彦在此基础上提出了神经认知机模型,这是一种分 层神经网络模型。 神经认知机由负责对比度提取的 G 层,以及负责 图形特征提取的S细胞层和抗变形的C细胞层交替排列组成。 最上层的 C 细胞会输出识别结果 。 S 细胞和C 细胞分别根据简单细胞和复杂细胞 的英语首字母得名。 借助于 S细胞层和 C细胞层交替排列的结构,各种 输入模式的信息会在经过 S 细胞层提取特征后,通过 C 细胞层对特征琦变的容错,并在反复迭代后被传播到上一层。 经过这个过程,在底层提取 的局部特征会逐渐变成全局特征 。 因输入模式扩大、缩小或平移而产生 的畸变也能很好地被 C 细胞消除,所以网络对变形具有较好的稳健性。
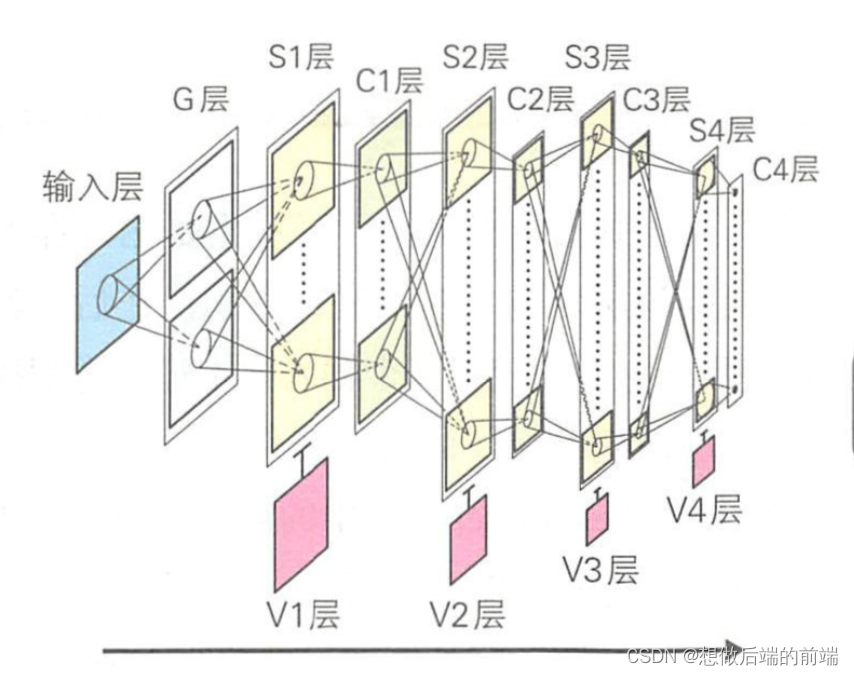
神经认知机中,如果没有任何细胞对输入模式做出反应,就采用增加细胞的学习规则。 通过引人神经网络中的误差反向传播算法,人们得 到了卷积神经网络( Convolutional Neural Network)。 LeCun 等人提出的卷积神经网络和神经认知机一样,也是基于人类视皮层巾感受野的 结构得到的模型。 如下所示,卷积神经网络由输入层( input layer)、卷积层( convolution layer )、池化层(pooling layer )、全连接层(fully connected layer )和输出层( output layer )组成。 通过增加卷积层和池化层,还可以得到更深层次的网络,其后的全连接层也可以采用多层结构 。
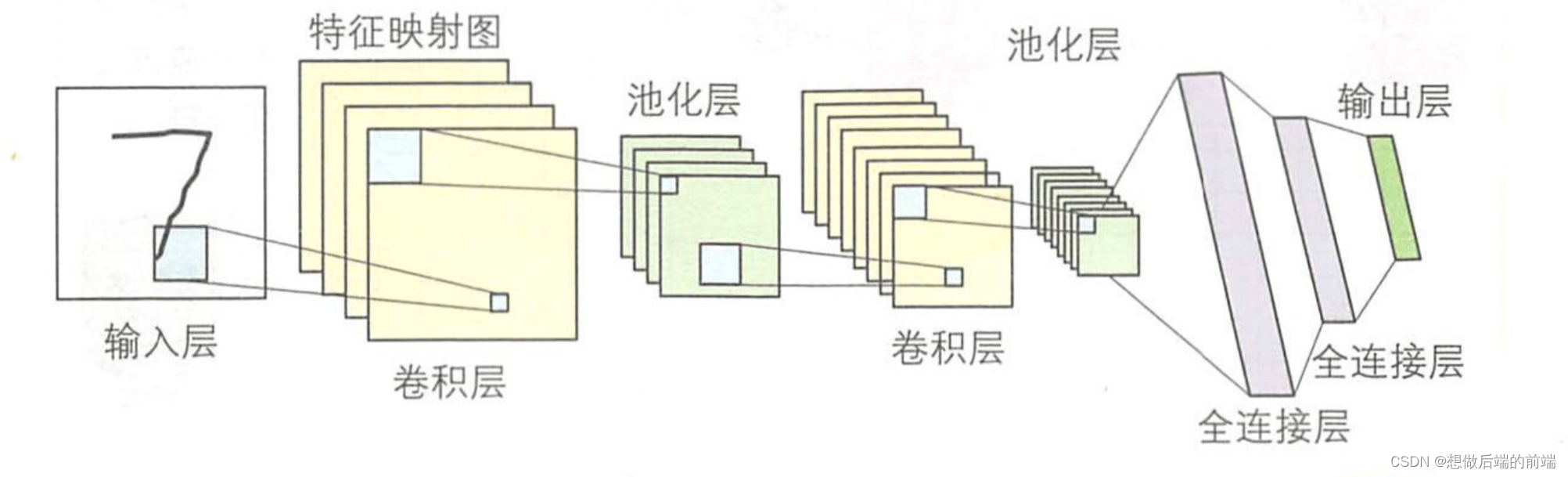
2、卷积层
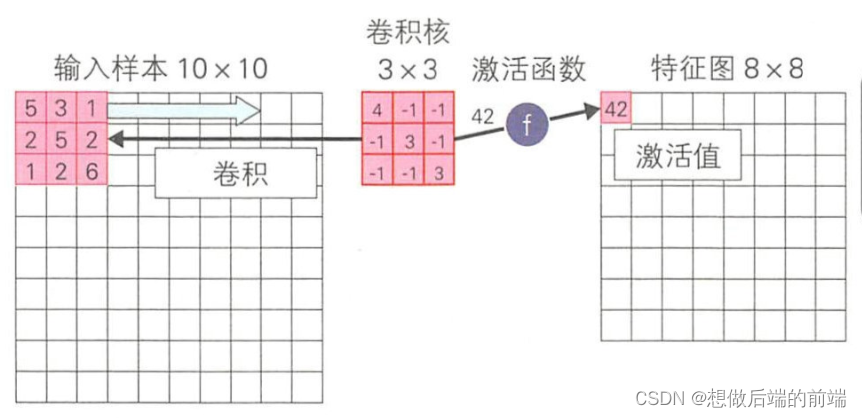
卷积神经网络中的卷积操作可以看作是输入样本和卷积核的内积运算 。 在第一层卷积层对输入样本进行卷积操作后 , 就可以得到特征图。 卷积层中是使用同一卷积核对每个输入样本进行卷积操作的。 在第二层及其以后的卷积层,把前一层的特征图作为输入数据,同 样进行卷积操作 。 该卷积操作与 Hubel-Wiesel 实验中的简单细胞具有相同 的作用。 如下图所示,对10 × 10的输入样本使用 3 × 3的卷积核进行卷 积操作后,可以得到一个 8 × 8 的特征图 。 特征阁的尺寸会小于输入样本, 为了得到和原始输入样本大小相同的特征图,可以采用对输入样本进行填充( padding)处理后再进行卷积操作的方法。 零填充( zero-padding)指 的就是用 0 填充输入样本的边界,填充大小为 P = (F -1)/2,其中 F 为 卷积核尺寸 。 在图 中,卷积核的滑动步长为 1。 我们也可以设定更 大的滑动步长,步快越大则特征图越小 。 另外,卷积结果不能直接作为特征图,需通过撒活函数计算后,把函数输出结果作为特征图 。
一个卷积层中可以有多个不同的卷积核,而每一个卷积核都对应一 个特征图 。

当卷积层的输入样本是三通道的彩色罔像时,卷积核就 会是三维的 3×M×M,M表示卷积核大小。 第二层及其以后的卷积层 的输入是上一层的特征图,而特征图的个数是由上一层的卷积核数决定 的。 例如, 当上一层的卷积核数为 8时,就会得到 8个特征图作为下一 层的输入,所以下一层需要 8个三维的 8×M×M卷积核。
3、池化层
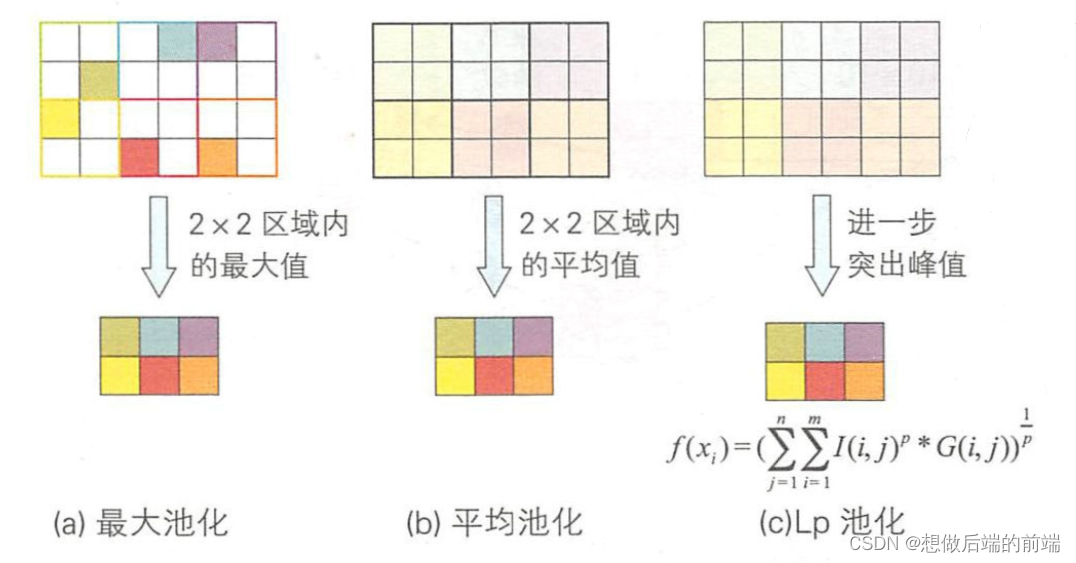
池化层的作用是减小卷积层产生的特征图的尺寸 。 选取一个区域, 根据该区域的特征图得到新的特征图,这个过程就称为池化操作 。 对一 个 2×2 的区域进行池化操作后,得到的新特征图会被斥缩为原来尺寸 的 1/4。 池化操作降低了特征图的维度,使得特征表示对输入数据的位置变化具有稳健性。 池化操作与 Hubel-Wiesel实验中的复杂细胞具有相同的作用。 主要的池化方法如下图 3所示。 其中最常使用的是图 (a) 所示的 最大池化, 最大池 化是选取图像区域内的最大值作为新的特征图。 另外还有图 (b)所示的平均池化,以及图 (c)所示的 Lp池化。 平均池化是取图像区域内的平均值作为新的特征图 。 Lp 池化则 是通 过突出图像区域内的中央值而计算新的特征图 。在图 (c)中的公式中,p越大越能突出中心位置的值。
4、全连接层
和多层感知器一样,全连接层也是首先计算激活值,然后通过激 活函数计算各单元的输出值 。 激活函数包括 sigmoid、 tanh、 ReLU 等函 数。 由于全连接层的输入就是卷积层或池化层的输出,是二维的特征图,所以需要对二维特征图进行降维处理

5、输出层
和多层感知器的输出层一样,卷积神经网络的输出层也是使用似然函数计算各类别的似然概率。 卷积神经网络出现后,最先被应用在了手写字符分类上。 手写字符识别用到的是 0到 9这 10个数字,所以共有 10个输出单元。 每个单元对应一个类别, 使用公式(5.1)的softmax函数可以计算输出单元的似然概率,然后把概率最大的数字作为分类结果输出
公式5.1:
在递归问题中, 一般使用线性输出函数(公式5.2)计算各单元的输出值。
公式5.2:
