数据挖掘之时间序列分析
一、 概念
时间序列(Time Series)
时间序列是指同一统计指标的数值按其发生的时间先后顺序排列而成的数列(是均匀时间间隔上的观测值序列)。
时间序列分析的主要目的是根据已有的历史数据对未来进行预测。
时间序列分析主要包括的内容有:趋势分析、序列分解、序列预测。
时间序列分解(Time-Series Decomposition)
时间序列按照季节性来分类,分为季节性时间序列和非季节性时间序列。
时间序列的构成要素:
-
长期趋势 T:现象在较长时期内受某种根本性因素作用而形成的总的变动趋势
-
季节变动 S:现象在一年内随着季节的变化而发生的有规律的周期性变动
-
循环趋势 C:现象以若干年为周期呈现出的波浪起伏形态的有规律的变动
-
不规则变动 I:是一种无规律可循的变动,包括严格的随机变动和不规则的突发性影响很大的变动两种类型
二、 非季节性时间序列
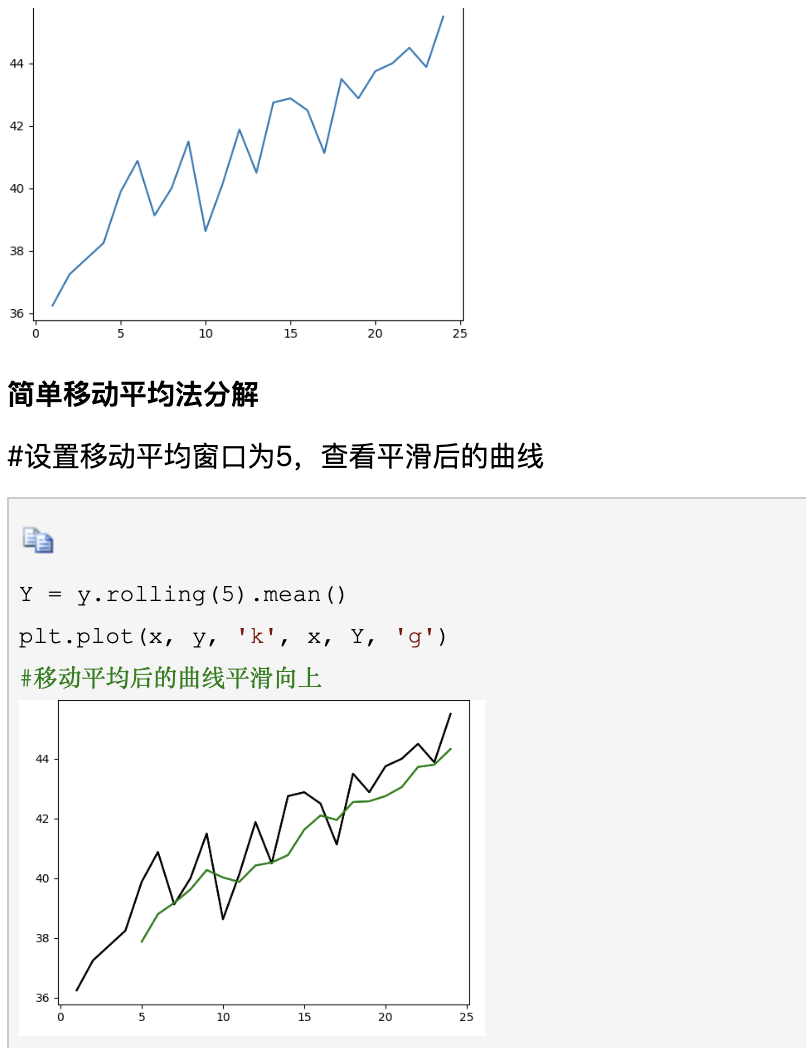
移动平均(MA,Moving Average)
移动平均是一种简单平滑技术,它通过在时间序列上逐项退役取一定项数的均值,来表现指标的长期变化和发展趋势
1、 简单移动平均(SMA)
简单移动平均将时间序列上前n个数值做简单的算术平均。
SMAn = ( x1 + x2 + …… + xn)/ n
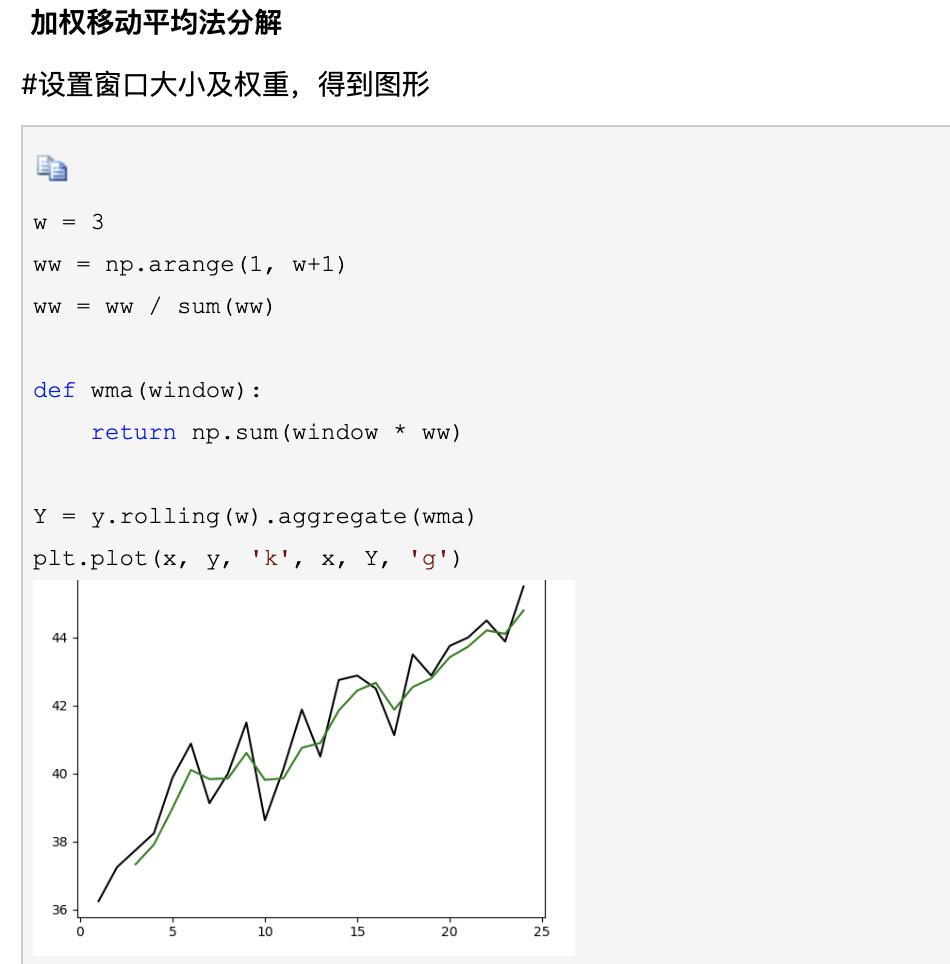
2、 加权移动平均(WMA)
加权移动平均,在基于简单移动平均的基础上,对时间序列上前n期的每一期数值赋予相应的权重,即加权平均的结果
基本思想:提升近期的数据、减弱远期数据对当前预测值的影响,使预测值更贴近最近的变化趋势。
WMAn = w1x1 + w2x2 + …… + wnxn
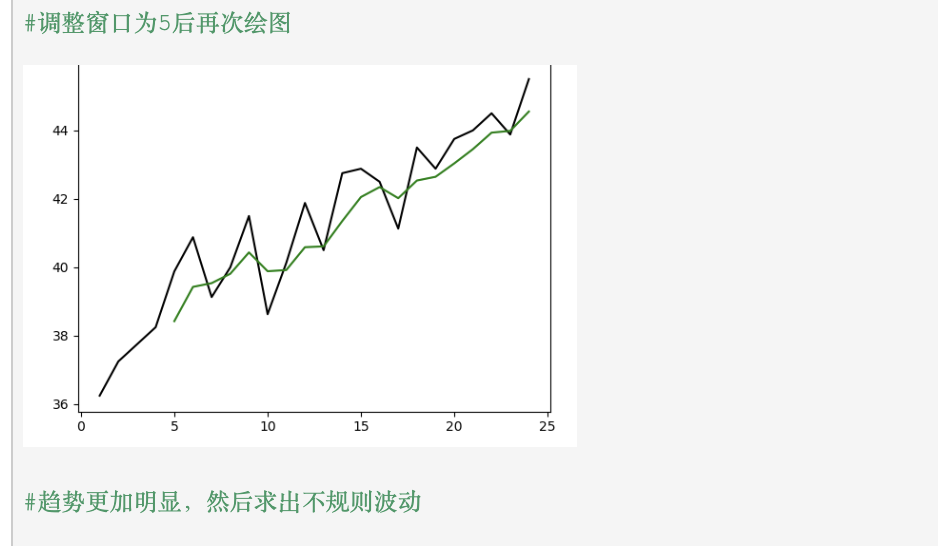
3、 非季节性时间序列的分解
将非季节性时间序列分解为 趋势 和 不规则波动 两个部分。
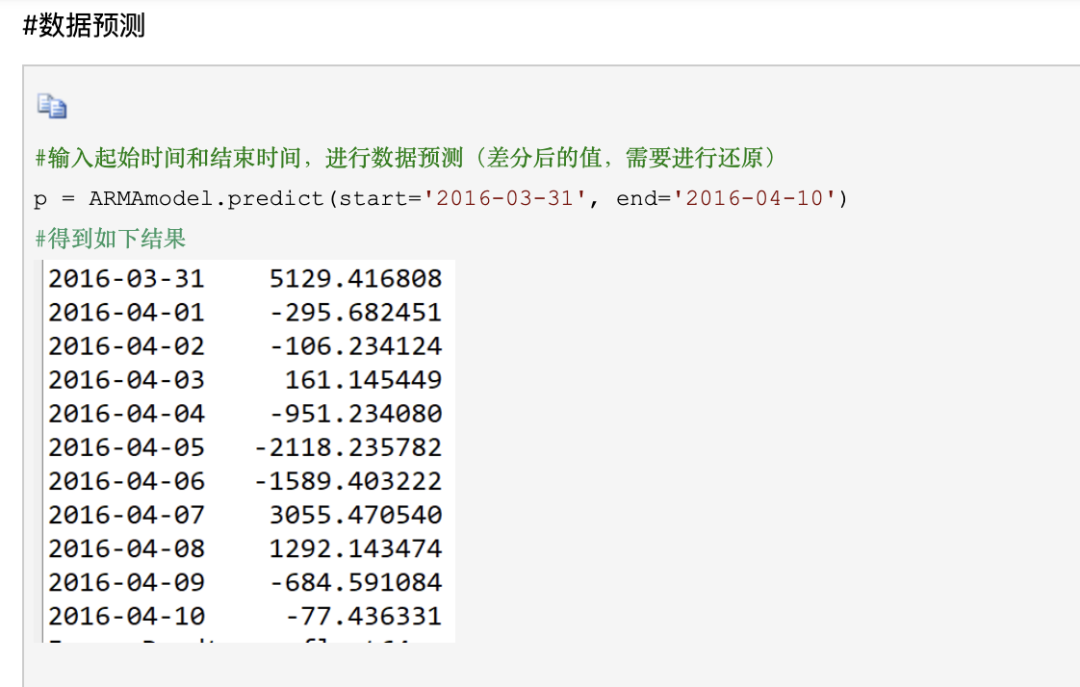
#导入数据并绘制图形,得到如下的图形
三、 季节性时间序列
在一个时间序列中,若经过n个时间间隔后呈现出相似性,该序列具有以n为周期的季节性特性。
季节性时间序列的分解
将季节性时间序列分解为 趋势 、周期性 和 不规则波动 三个部分。
tips:需要将时间列转换成索引列,方便计算

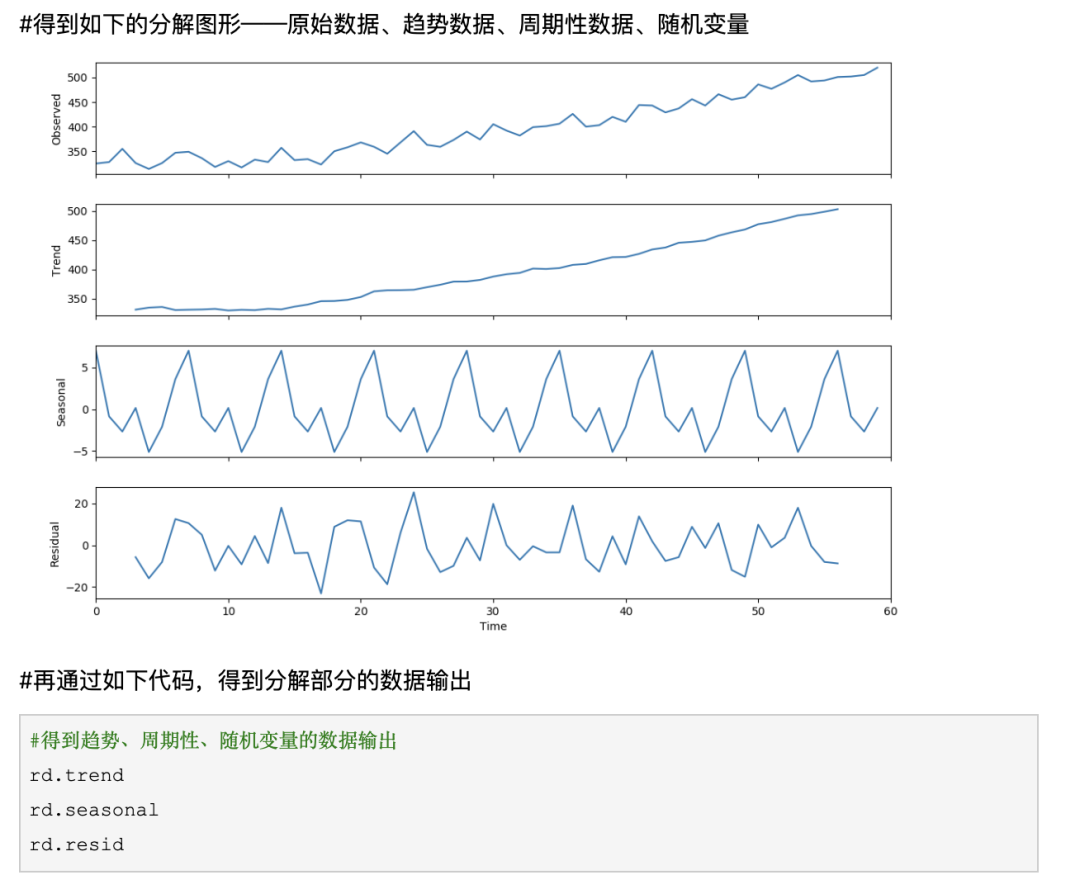
四、 序列预测
1、概念
预测(forecast)
对尚未发生或目前还不明确的事物进行预先的估计和推测,是在现时对事物将要发生的结果进行探讨和研究,简单的说就是指从已知事件预测未知事件。
时间序列预测(Time Series Forecasting
通过分析时间序列,根据时间序列所反映出来的发展过程、方向和趋势,进行类推或延申,借以预测下一段时间或以后若干时间段内可能达到的水平。
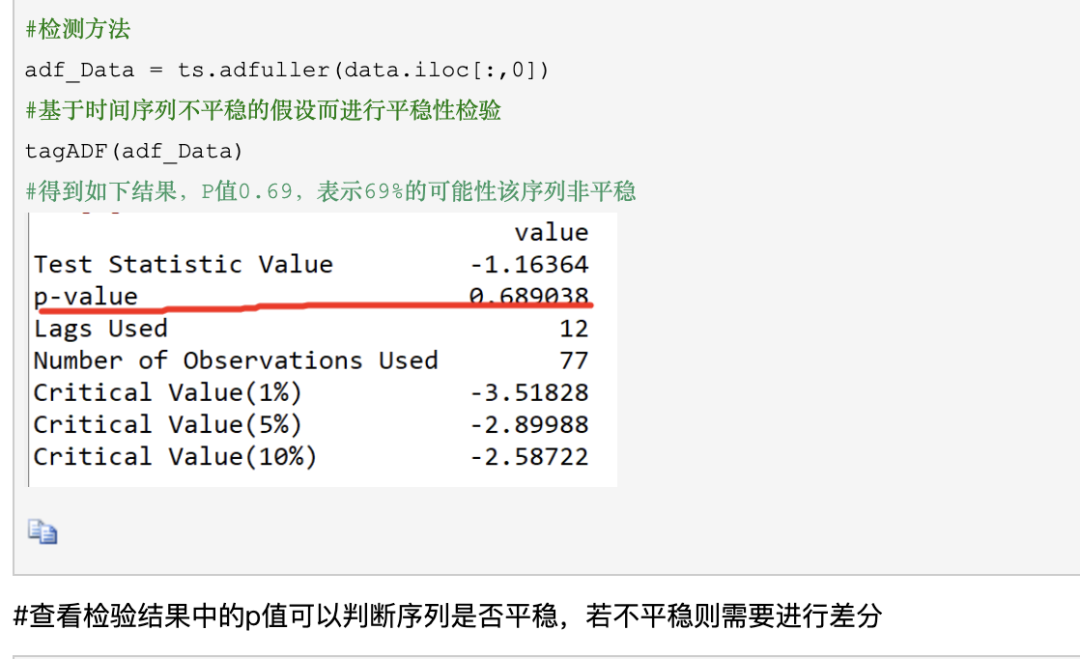
平稳型时间序列(Stationary Time Series)
平稳时间序列,其统计特征不随时间变化二变换,一般采用均值、方差或者协方差来作为统计特征。
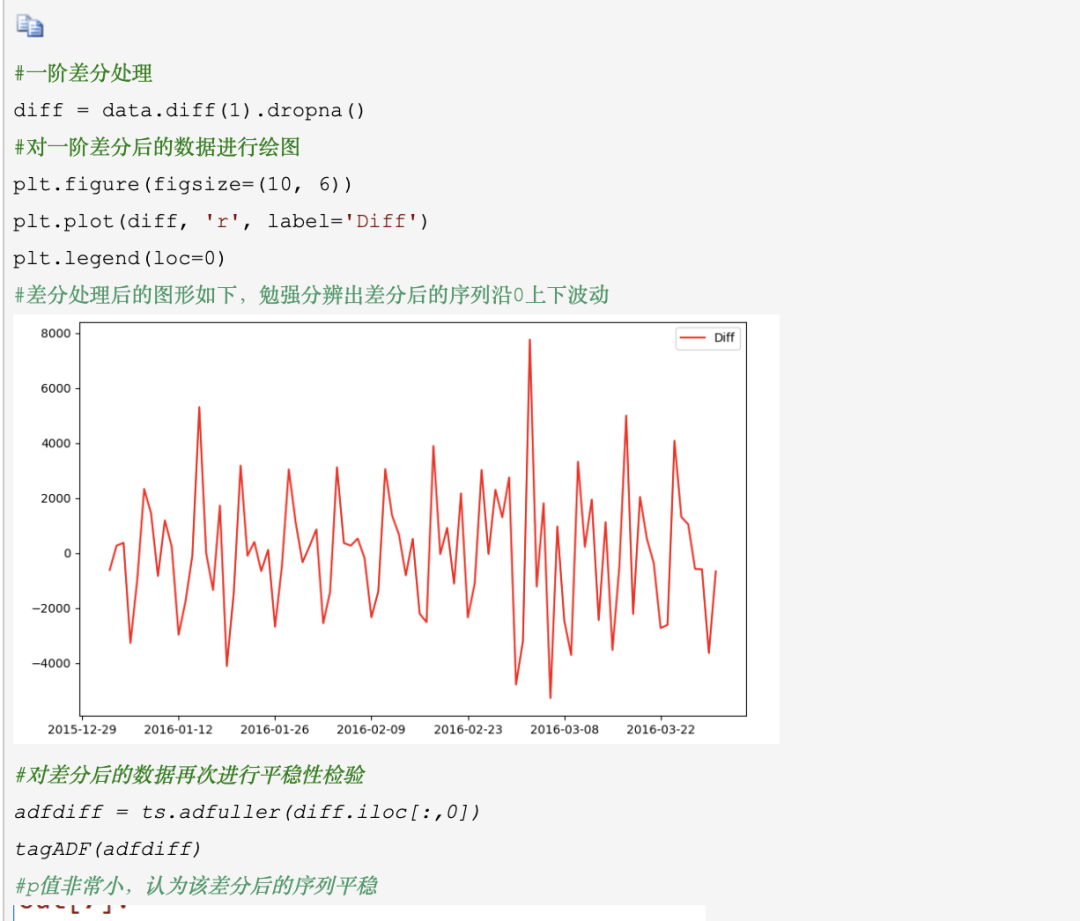
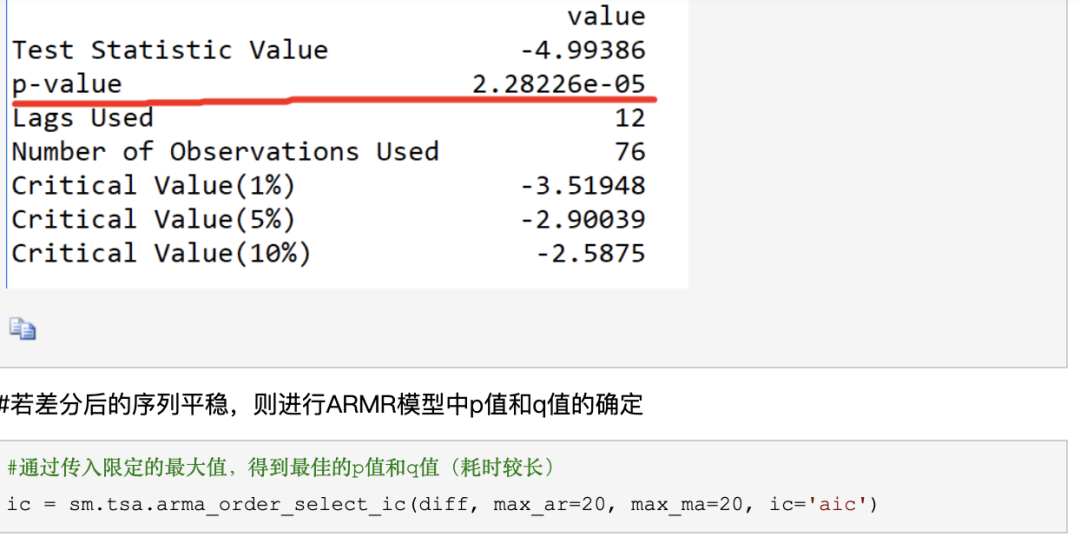
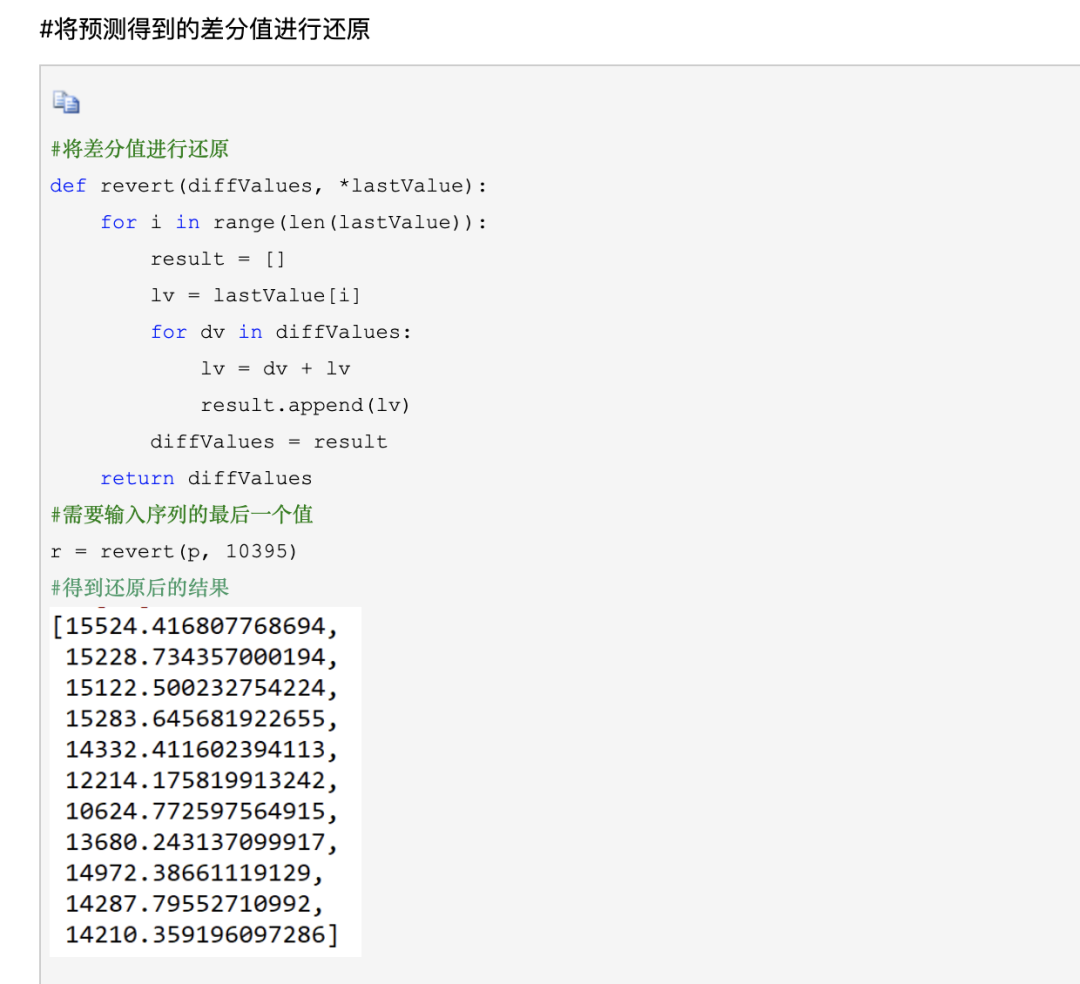
差分(Integrated)

常用的时间序列预测模型:
AR(p)模型(Autoregressive Model):自回归模型描述的是当前值与历史值之间的关系
MA(q)模型(Moving Average Model):移动平均模型描述的是自回归部分的误差累计
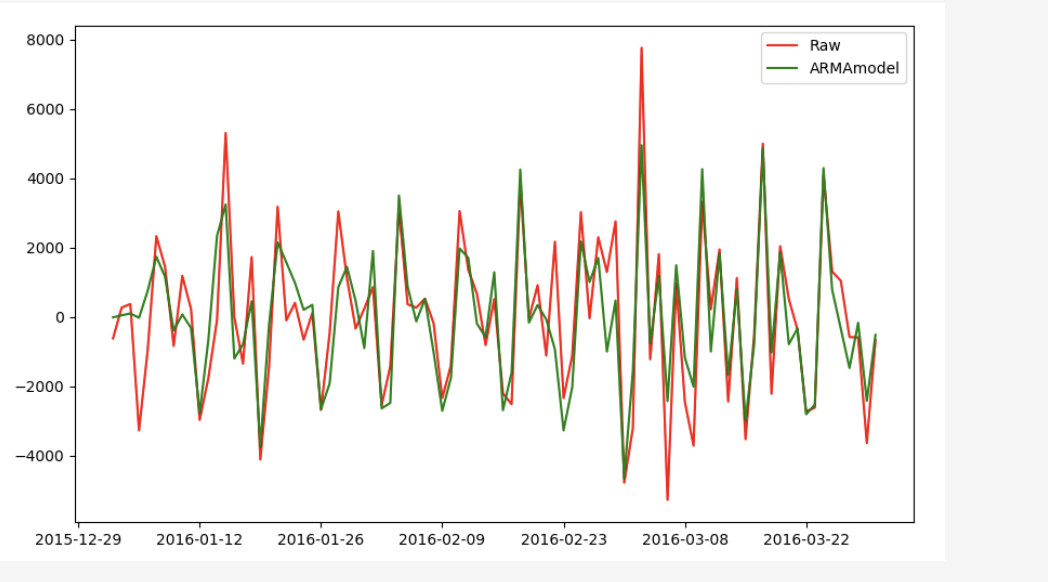
ARMA模型:所谓ARMA模型,是指将非平稳时间序列转化为平稳时间序列,然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。