当前位置：首页 > article >正文

leetCode 39.组合总和 + 回溯算法 + 剪枝 + 图解 + 笔记

article 2024/9/23 3:32:27

39. 组合总和 - 力扣（LeetCode）

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合

candidates 中的 同一个 数字可以 无限制重复被选取
如果至少一个数字的被选数量不同，则两种组合是不同的

对于给定的输入，保证和为 target 的不同组合数少于 150 个

示例 1：

输入：candidates = [2,3,6,7], 
target = 7

输出：[[2,2,3],[7]]
解释：2 和 3 可以形成一组候选，2 + 2 + 3 = 7 。注意 2 可以使用多次。
7也是一个候选，7 = 7 。仅有这两种组合。

示例 2：

输入: candidates = [2,3,5], target = 8
输出: [[2,2,2,2],[2,3,3],[3,5]]

示例 3：

输入: candidates = [2], target = 1
输出: []

思路和分析：对比 77. 组合 - 力扣（LeetCode）和 216. 组合总和 III - 力扣（LeetCode），和本题的区别，本题没有数量要求，且可以无限重复，但是受到总和限制，故间接的限制了个数

（一）回溯算法

>>回溯三部曲:

1).确定回溯函数参数

path来收集符合条件的结果
result 保存 path,作为结果集
startIndex 来控制for循环的起始位置

>>注意(来自代码随想录Carl老师的总结：代码随想录 (programmercarl.com))

如果是一个集合来求组合的话，就需要startIndex：77. 组合 - 力扣（LeetCode）和 216. 组合总和 III - 力扣（LeetCode）
如果是多个集合取组合，各个集合之间相互不影响，那么就不用 startIndex：17. 电话号码的字母组合 - 力扣（LeetCode）

vector<vector<int>> result;
vector<int> path; 
void backtracking(vector<int>& candidates,int target,int sum,int startIndex) {

2).递归的终止条件

if (sum > target) {
    return;
}
if (sum == target) {
    result.push_back(path);
    return;
}

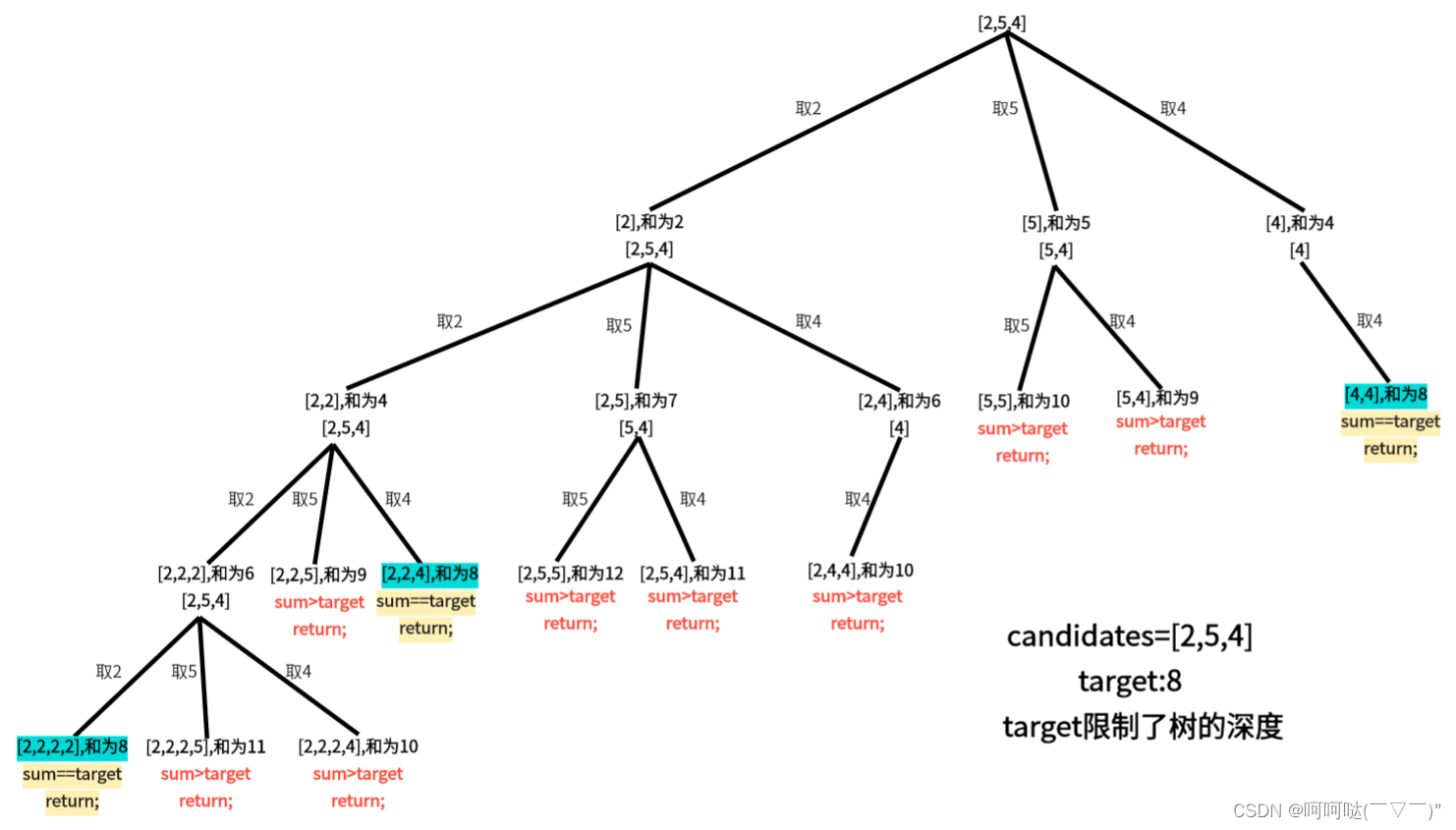3).单层搜索的逻辑

单层 for 循环依然是从 startIndex 开始，搜索 candidates 集合。
为了实现重复选取，backtracking 的时候传入的 startIndex 是 i ，而不是 i + 1。比如在本层已经使用了 "2"，下一层依然可以取到 i

for (int i = startIndex; i < candidates.size(); i++) {
    sum += candidates[i];
    path.push_back(candidates[i]);
    backtracking(candidates, target, sum, i); // 关键点:不用i+1了，表示可以重复读取当前的数
    sum -= candidates[i];   // 回溯
    path.pop_back();        // 回溯
}

C++代码：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum > target) {
            return;
        }
        if (sum == target) {
            result.push_back(path);
            return;
        }

        for (int i = startIndex; i < candidates.size(); i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i); // 不用i+1了，表示可以重复读取当前的数
            sum -= candidates[i];
            path.pop_back();
        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

对 sum>target 这种情况，其实还是进入了下一层递归，只是下一层递归结束判断的时候，发现sum > target 就返回（结束本层递归），这里可以做优化，接着往下看！

（二）剪枝操作

我们看这张图，是candidates为[2,4,5] ，而上图是candidates为[2,5,4]，它们绿色节点出现的位置并不一样，发现下图排完序之后，若能找到符合的节点，其实是当前同层的前面是没有不符合的节点的。（描述可能有点问题，大家可以对比一下找规律）

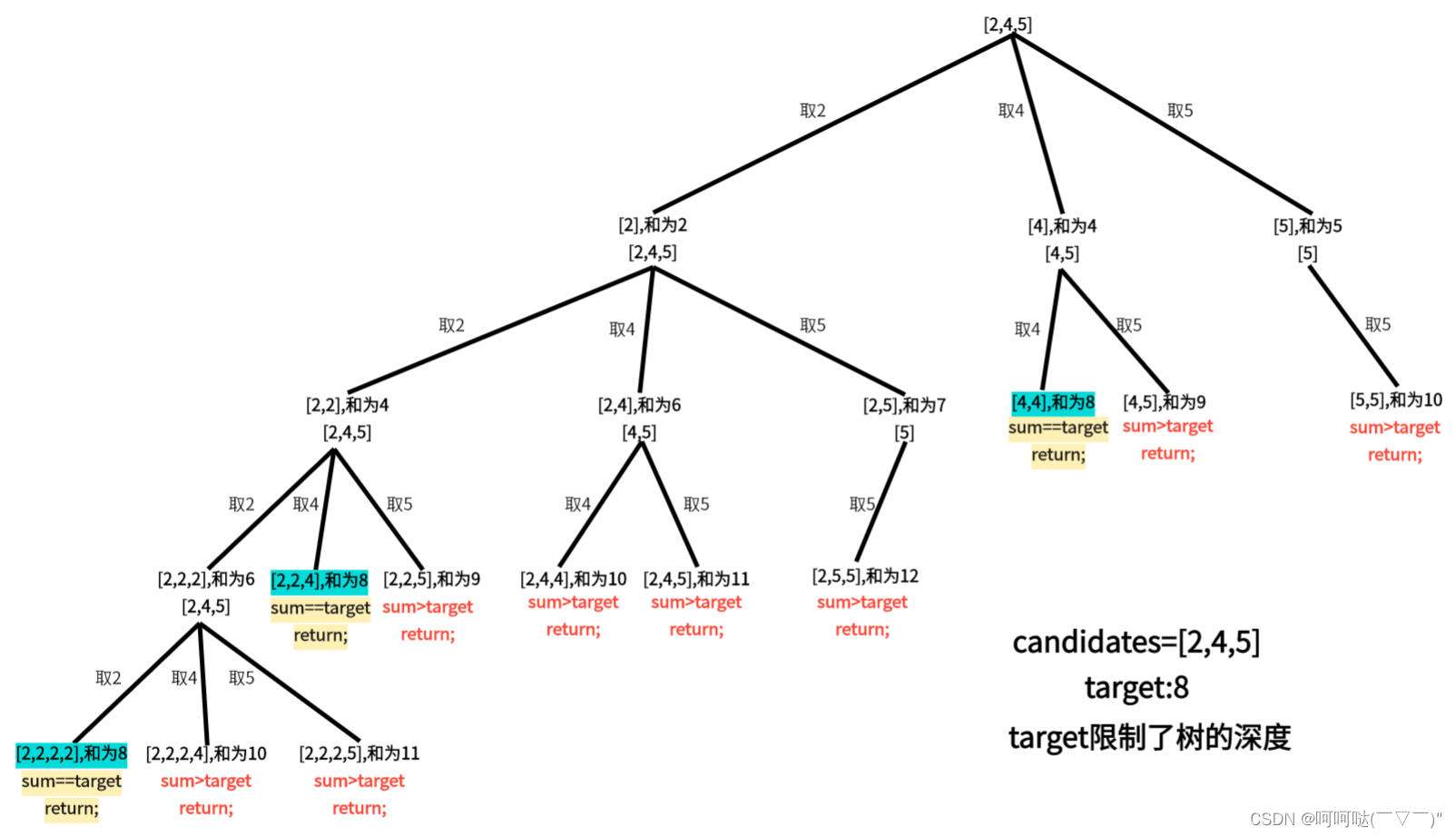
其实如果已经知道下一层的sum > target，就没必要再进入下一层递归了

1.在求和问题中，排序之后加剪枝是常见的套路，所以candidates需要先排序，后剪枝

sort(candidates.begin(), candidates.end()); // 需要排序

2.for循环剪枝：

for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)

C++代码：

class Solution {
private:
    vector<vector<int>> result;
    vector<int> path;
    void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
        if (sum == target) {
            result.push_back(path);
            return;
        }

        // 如果 sum + candidates[i] > target 就终止遍历
        for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
            sum += candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates, target, sum, i);
            sum -= candidates[i];
            path.pop_back();

        }
    }
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        result.clear();
        path.clear();
        sort(candidates.begin(), candidates.end()); // 需要排序
        backtracking(candidates, target, 0, 0);
        return result;
    }
};

（三）减少一个参数

class Solution {
public:
    vector<vector<int>> result;
    vector<int> path; 
    void backtracking(vector<int>& candidates,vector<int> path,int target,int startIndex) {
        if(target == 0){
            result.push_back(path);
            return;
        }
        for(int i=startIndex;i<candidates.size() && target-candidates[i] >= 0;i++) {
            target -= candidates[i];
            path.push_back(candidates[i]);
            backtracking(candidates,path,target,i);
            target += candidates[i];
            path.pop_back();
        }
    }

    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end()); // 需要排序
        backtracking(candidates,path,target,0);
        return result;
    }
};

参考和推荐文章、视频：

代码随想录 (programmercarl.com)https://www.programmercarl.com/0039.%E7%BB%84%E5%90%88%E6%80%BB%E5%92%8C.html#%E6%80%9D%E8%B7%AF带你学透回溯算法-组合总和（对应「leetcode」力扣题目：39.组合总和）| 回溯法精讲！_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV1KT4y1M7HJ/?spm_id_from=333.788&vd_source=a934d7fc6f47698a29dac90a922ba5a3