当前位置：首页 > article >正文

初识动态规划算法(题目加解析)

article 2024/11/13 10:11:12

文章目录

什么是动态规划
正文
- 力扣题
- - 第 N 个泰波那契数
  - 三步问题
  - 使用最小花费爬楼梯
总结

什么是动态规划

线性动态规划：是可以用一个dp表来存储内容，并且找到规律存储,按照规律存储。让第i个位置的值等于题目要求的答案
>dp表：dp表就是用一个连续的空间存储需要存储的有规律的值。

干说无力直接正文

正文

力扣题

第 N 个泰波那契数

题目:地址
题目解析:
在这里插入图片描述

给定了三个数 T0,T1,T2
求Tn的值
**根据题意可以翻译成 Tn = Tn-1+Tn-2+Tn-**3

动态规则的题目都可以分五步
1、状态表示(★)
状态表示是必须要会的并且理解的
>一般的状态表示是:经验+题目解析
经验是要多写才能得出来的
这个题目的状态表示已经给出来了
Tn的值是前三个值的合
2、状态转移方程(★)
状态转移方程一般可以表示成第n个值=····
题目已经给出Tn=Tn-1+Tn-2+Tn-3
3、初始化
把dp表初始化成0
4、填dp表顺序
从左往右填
5、返回值
dp[n]

代码答案：

class Solution {
public:
    int tribonacci(int n) 
    {
        if(n==0)
       {
           return 0;
       }
        if(n==1||n==2)
        {
            return 1;
        }
        // vector<int> dp(n+1);
        // dp[0]=0,dp[1]=1,dp[2]=1;
       
        // for(int i =3;i<=n;i++)
        // {
        //     dp[i]=dp[i-1]+dp[i-2]+dp[i-3];
        // }
        //空间优化
        int a= 0,b=1,c=1,d=0;
        for(int i =3;i<=n;i++)
        {
            d=a+b+c;
            a=b;
            b=c;
            c=d;
        }
        return d;
    }
};

三步问题

题目:地址
题目解析:
在这里插入图片描述
题目解释:

这个小男孩一小子可以走 1层/2层/3层
走到第n层的时候有多少种方法
如果结果太大需要%1000000007

动态规划的五步走:
1、状态表示(★)
这个题目的状态表示是

2、状态转移方程(★)
依照上面的解释
动态方程为Tn = Tn-1+Tn-2+Tn-3
3、初始化
初始化dp表为0
4、存储dp表的顺序
从左往右
5、返回值
dp[n]

代码:

class Solution {
public:
    int waysToStep(int n) 
    {
        if(n==1||n==2)
        {
            return n;
        }
        if(n==3)
        {
            return 4;
        }
        // vector<int> dp(n+1);
        // dp[1] = 1,dp[2]=2,dp[3]=4;
        //空间优化
        int a =1,b=2,c=4,d=0;
        for(int i = 4 ;i<=n;i++)
        {
            //dp[i]=((dp[i-1]+dp[i-2])%1000000007+dp[i-3])%1000000007;
            d=((a+b)%1000000007+c)%1000000007;
            a=b;
            b=c;
            c=d;
        }
        return d;
    }
};

使用最小花费爬楼梯

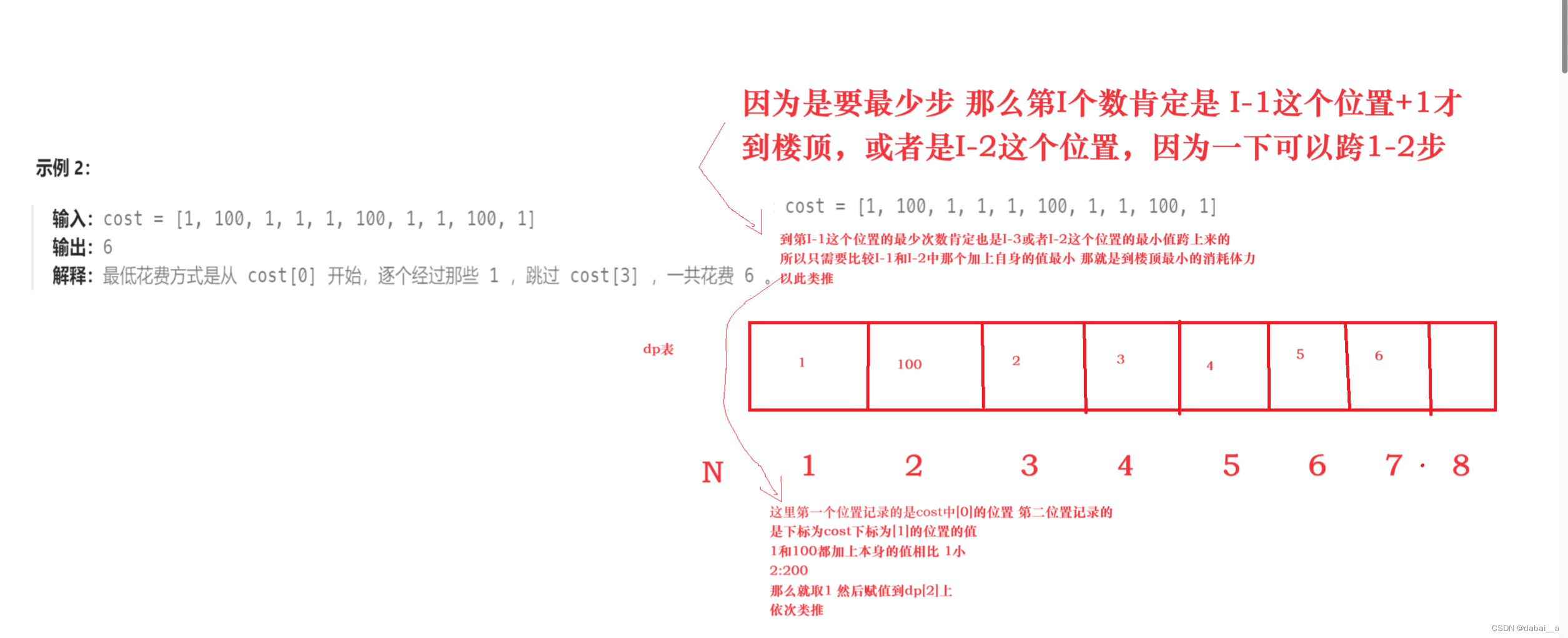
题目:地址
题目解析:
在这里插入图片描述
题目解释:

一个人一下可以走1-2步
最少需要花费多少体力到楼顶
这里的楼顶不是传过来的字符串的位置
因为如果是传过来的字符串的位置那么应该不用+他的值
但是用例1来说
10直接2步到10应该是最快的
但是解释是15
所以楼顶的位置应该在传过来字符的后一个位置

五步走:

1、状态表示

2、状态转移方程
方程是:dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2])
3、初始化
把dp表初始化
4、存入dp表的位置
从做向右
5、返回值
返回dp[i]位置的值

代码:

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) 
    {
        vector<int> dp(cost.size()+2);
        for(int i =2;i<=cost.size();i++)
        {
            dp[i]=min(cost[i-1]+dp[i-1],cost[i-2]+dp[i-2]);
        }
        return dp[cost.size()];
    }
};