java第三天
感觉java现在这几节课讲的和c语言差不多
不太一样
比如这个就是一样的
int i=10;
i+=20;
i=20+i;这个就不一样,需要类型转化
short s=10;
s+=20;//这个没有问题
s=s+20;就是说+=包含了一个强制转化的符号
下面就是写的几个递归题目
# 数楼梯
## 题目描述
楼梯有 $N$ 阶,上楼可以一步上一阶,也可以一步上二阶。
编一个程序,计算共有多少种不同的走法。
## 输入格式
一个数字,楼梯数。
## 输出格式
输出走的方式总数。
## 样例 #1
### 样例输入 #1
```
4
```
### 样例输出 #1
```
5
```
## 提示
- 对于 $60\%$ 的数据,$N \leq 50$;
- 对于 $100\%$ 的数据,$1 \le N \leq 5000$。
题解:这个要注意就是要用高精度加起来,因为后面数据太大了 a【阶梯】【数据的第几个】
#include <stdio.h>
int a[5001][5001];
int len=1;
void hb(int n)
{
for(int i=1;i<=len;i++)
{
a[n][i]=a[n-1][i]+a[n-2][i];
}
for(int i=1;i<=len;i++)
{
if(a[n][i]>=10)
{
a[n][i+1]+=a[n][i]/10;
a[n][i]=a[n][i]%10;
if(a[n][len+1]) len++;
}
}
}
int main()
{
int n;
scanf("%d",&n);
a[1][1]=1;
a[2][1]=2;
for(int i=3;i<=n;i++)
{
hb(i);
}
for(int i=len;i>=1;i--)
{
printf("%d",a[n][i]);
}
}# [NOIP2002 普及组] 过河卒
## 题目描述
棋盘上 $A$ 点有一个过河卒,需要走到目标 $B$ 点。卒行走的规则:可以向下、或者向右。同时在棋盘上 $C$ 点有一个对方的马,该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。
棋盘用坐标表示,$A$ 点 $(0, 0)$、$B$ 点 $(n, m)$,同样马的位置坐标是需要给出的。
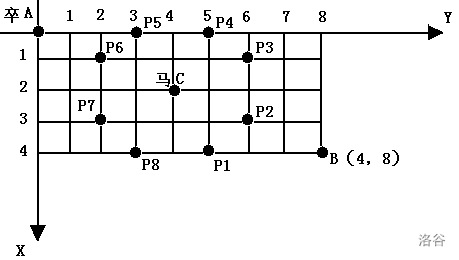
现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数,假设马的位置是固定不动的,并不是卒走一步马走一步。
## 输入格式
一行四个正整数,分别表示 $B$ 点坐标和马的坐标。
## 输出格式
一个整数,表示所有的路径条数。
## 样例 #1
### 样例输入 #1
```
6 6 3 3
```
### 样例输出 #1
```
6
```
## 提示
对于 $100 \%$ 的数据,$1 \le n, m \le 20$,$0 \le$ 马的坐标 $\le 20$。
**【题目来源】**
NOIP 2002 普及组第四题
#include <stdio.h>
long long fa[100][100];//棋盘0就是ok,1就是不ok
int pan[100][100];
int ma[9]={0,1,2,2,1,-1,-2,-2,-1};//x坐标
int ma1[9]={0,2,1,-1,-2,-2,-1,1,2};//y坐标
int main()
{
int i,j;
int n,m,x,y;
scanf("%d%d%d%d",&n,&m,&x,&y);//坐标
n+=2;m+=2;x+=2;y+=2;
fa[2][1]=1;//出口
for(i=1;i<=9;i++)
{
pan[x+ma[i]][y+ma1[i]]=1;
}
for(i=2;i<=n;i++)
{
for(j=2;j<=m;j++)
{
if(pan[i][j]) continue;//找到是1就过
fa[i][j]=fa[i-1][j]+fa[i][j-1];
//printf("%lld %d %d\n",fa[i][j],i,j);
}
}
printf("%lld",fa[n][m]);
}放假放假准备后天回家nice
