当前位置：首页 > article >正文

【DP动态规划】最长子序列

article 2025/1/10 13:11:25

问题描述：

解题分析：

采用 DP 动态规划的方法：

先设置 f（1）=1；

其次在计算出 f（2），再依次计算出后续的 f 的数值

例F(3)是如何计算出来的：

首先判断a【3】是否大于a【1】，确实大于，故F（3）=F（1）+ 1 = 2；

再判断a【3】是否大于a【2】，不大于，不操作

但是需要注意的是，如果a【2】=1.5，那么F（3）=F（2）+ 1 = 2 + 1 = 3【此时F（3）的数值需

要更新】

如下图：

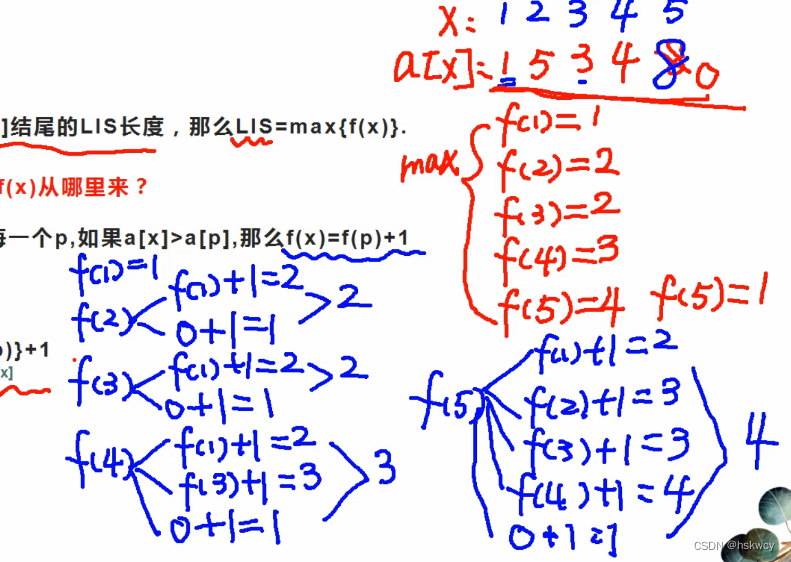
按照这个规律依次计算即可；

解题代码：

//最长上升子序列 
#include <bits/stdc++.h>
using namespace std;
const int vinf = 1e6+100;
int lin[vinf];    //最大空间
int val[vinf]; 
int main(){
	int n;
	cin>>n;
	for(int i=1;i<=n;++i){
		cin>>lin[i];
	}
	val[1]=1;  //初始起点 
	//读取完数组，开始处理
	for(int i=2;i<=n;++i){
		int pp=0;     //用来记录循环比较时最大的那个数，每一轮都要初始化为0 
		for(int j=1;j<i;++j){
			//依次比较
			if(lin[i]>lin[j]){
				if(val[j]+1 >= pp){
					pp = val[j]+1;
				}
			} 
		}
		val[i]=max(1,pp);
	}
	int ans=-1;
	for(int i=1;i<=n;i++){
		if(val[i]>ans)
			ans=val[i];
	}
	cout<<ans<<endl;
	return 0;
}