rcssci包横空出世，限制性立方样条全自动切点靓图

z致敬前辈:R语言统计与绘图

仅以本篇2800字真文一并纪念工作11年来潦倒的收入、间歇的鸡血、憋屈的倔强、幽暗的过往和心中的远方。

1 缘起

Restricted cubic splines (RCS)近年来火遍各类SCI期刊，初次接触的小伙伴们可以去搜索笔者前期的2篇RCS文章补充一下基础知识（链接）。笔者撰写SCI时候也经常苦恼，即使有代码积累但依然每次都要修改长长的代码，精雕细琢的修改图形参数，而且随着变量越多需要修改的就越多。忽然有一天，笔者想，为何不自己开发一个R包，这样你爽我爽大家爽不好吗？笔者搜索google与网上教程，RCS图形不够优美也没有OR/HR参考线条及不同形态cutoff的选取介绍（貌似深度思考的文章就属本公众号了），仅有的R包ggrcs也是过于简单且密度图错误Y2轴非动态比例。于是，笔者本着对小伙伴们负责任的精神说干就干，开发了rcssci包。至于为什么叫rcssci，后面3个字母你懂的。

2. 论文中常见RCS图形型态及切点选取

本章开始，还是要再总结升华一下RCS的型态与切点概念，rcssci包就是基于不同型态进行了4套图形的同步输出。

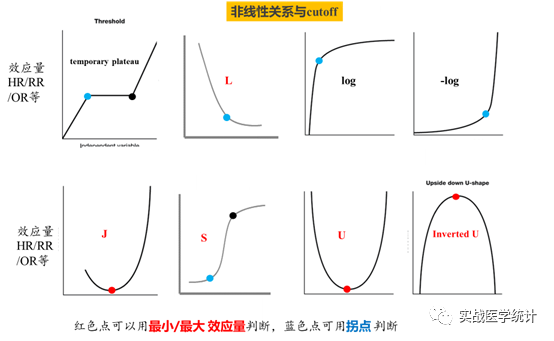
2.1  U/∩/L型态3种类

非线性关系常见U型、倒U (∩) 型、J型以及S型，4者均可依据肉眼形态判断近似最符合的形态，但是有时候L与J型曲线区分的并不是很清楚，需要测试是否最后有翘尾。笔者将非线性型态总结为泛u型(U/J)、泛∩型、泛L型(平原/L/log/-log/S)，对应ushap、nshap、lshap等3种输出图。R下图中红色点可通过效应量OR/HR最小或最大实现，蓝色点通过断点实现。

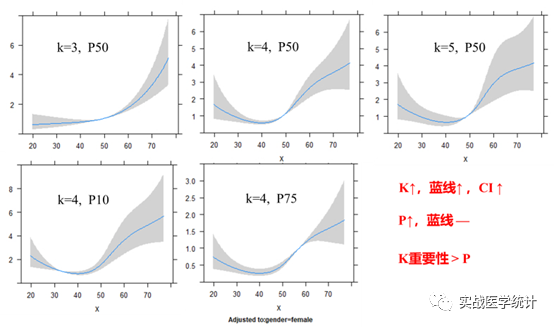
2.2  knot与波动参数refvalue

Knot(缩写K)一般选3-7，K选3或4最常见。有时候K=7变的太复杂，如果AIC十分接近，可以降低K到4-5等。K很重要，会严重影响RCS主拟合线和95%CI形态，Quantiles(缩写Q)也会影响RCS主拟合线和95%CI的形态。K的获取是拟合K 3-7后模型AIC min对应的K。设定好K数后，rms函数会拟合默认的knot节点+分位数Q，例如knot=3，自动拟合的是Q10、Q50、Q90。此时K绑定Q分位数。少见一些论文值得的会代码修改knot中的Q位置。如要手动修改代码见下图中。

指定K+默认Q参数后，再思考95%CI位置参数(波动)refvalue。Refvalue同时改变了阴影位置及波动的型态。当位置参数refvalue未明确的时候，默认是变量x的中位数，即refvalue=prob 0.5=P50；refvalue也可设为第1十分位数，即P10=prob 0.1时，如下图。rrcssci包总结了3型态2趋势场景：

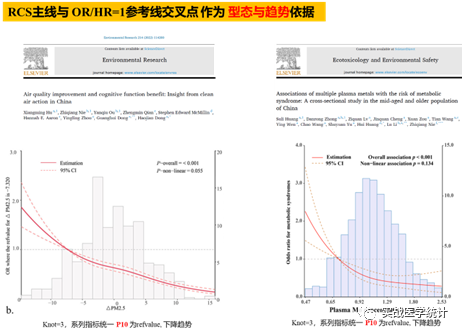
①表达下降或上升趋势，选择prob(下图中P)相对位置。例如文献https://doi.org/10.1016/j. ecoenv.2022.113183，选择prob=0.1即P10。②表达U/∩/L型切点cutoff处出现趋势逆转，rcssci包会默认输出cutoff值并记录在y轴标签。

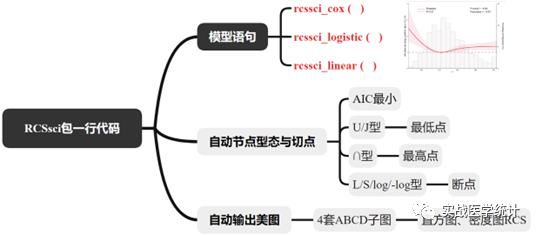
3. rcssci包适用范围图形规则

rcssci包V1.0版核心函数有3个，rcssci_cox、rcssci_logistic、rcssci_linear，分别适合于模型为等比例风险cox模型，经典二分类logistic和一般线性模型。前2者y轴为效应量HR、OR；后者y轴为原始y。rcssci包V1.0版Y为OR/HR/y效量非线性剂量关系，拟合理想的结果笔者概况为：

①剂量关联呈现出典型的非线性U型、倒U型、J型、直线型等型态；②线性关联，呈现上升趋势或下降趋势；③非线性关联探索cutoff，将x变量2分、3分类，再进行后续分段/组分析。

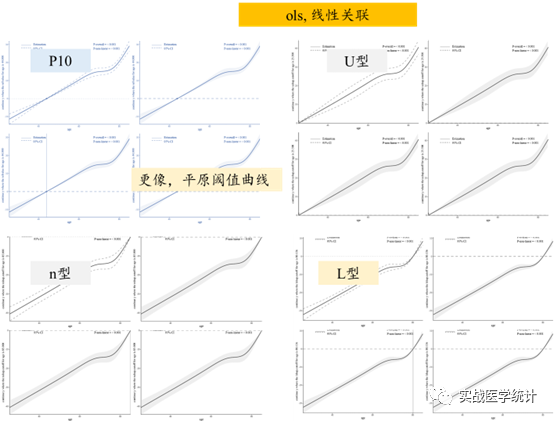
rcssci包在工作目录(setwd对应的文件夹)下自动输出4套RCS双坐标图(PDF版，方便大家后续ppt编辑)，图例包括总P值、非线性趋势P值，切点包括U型、∩型、及L型等等非线性形态切点的自动获取。4套RCS双坐标图分别为：fig.proball.pdf，fig.ushapall.PDF，fig.nshapall.PDF，fig.lshapall.PDF。①fig.proball.pdf，ABCD子图，均为位置参数refvalue=prob时RCS趋势图。②fig.ushapall.PDF，ABCD子图，均为位置参数refvalue=prob时可能的更具有解释性的U型(U/J)图。③fig.nshapall.PDF，ABCD子图，均为位置参数refvalue=prob时可能的更具有解释性的倒U(n)型图。④fig.lshapall.PDF，ABCD子图，均为位置参数refvalue=prob时可能的更具有解释性的L(L/平原/log/-log/S)型图。rcssci_cox、rcssci_logistic可以输出带直方图或密度图的双坐标图，rcssci_linear则不输出直方图或密度图。

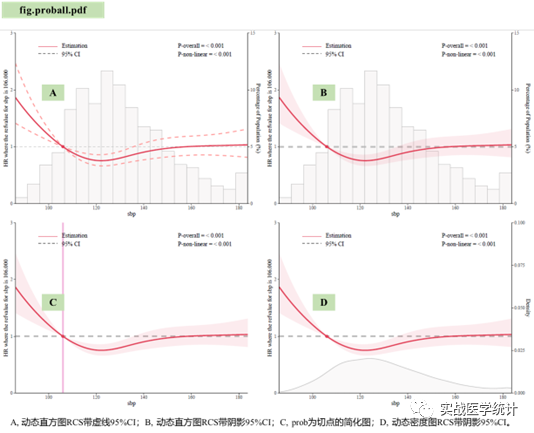
RCS判定规则与步骤如下：

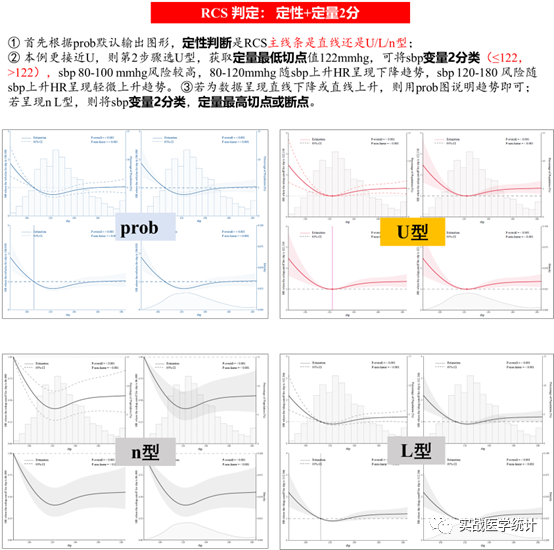
4 rcssci包实战案例与代码

rcssci包V1.0版核心函数有3个，rcssci_cox、rcssci_logistic、rcssci_linear。笔者内置了团队数据sbpdata.rdata文件（论文发表中，故仅选择性抽取了原始数据10%）为纵向数据的SBP收缩压与全因死亡关联数据。以下实战中原始sbpdata.rdata 不等于包内置sbpdata.rdata (仅为了达到Rpackage上传需要5s内演算要求)。

4.1 实战cox分析

加载rcssci包后，一行命令搞定cox分析rcs绘制，prob推荐0.1，不写默认0.5。

rcssci_cox(data=sbpdata, y = "status",x = "sbp",covs=c("age","gender"),time = "time", prob=0.1)

RCS一行代码输出四套图，见上述《RCS判定规则与步骤》。

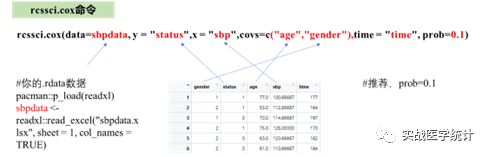
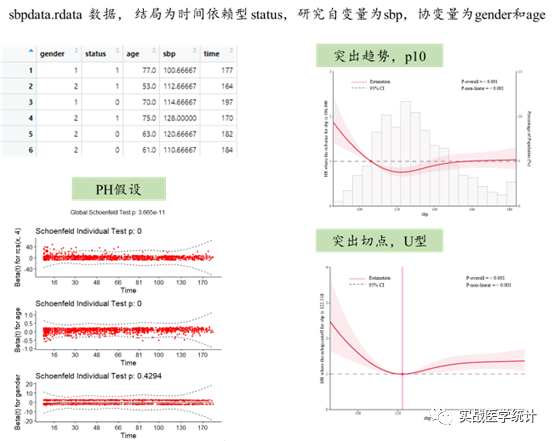
过程解析：rms包做RCS默认prob=0.5中位数。但是很多时候图形跑出来并非均衡对称。这时候，灵活无敌可爱的rcssci，可以仿照模板论文设定prob位置参数(笔者建议设定prob=0.1)进行趋势与cutoff的自动输出了。本例AIC最小原则，自动选择knot=4，采用默认Q分位数为0.05 0.35 0.65 0.95。结果解析：在setwd()工作路径下，自动输出4套RCS双坐标图分别为：fig.proball.pdf，fig.ushapall.PDF，fig.nshapall.PDF，fig.lshapall.PDF。本例研究结果为：P-overall<0.001，P non-linear <0.001，表明总的检验有意义，非线性关联检验也有意义，呈现出Ushap关联。由于最高点不呈现n型分布本数据不适合采用n型态，由于右侧拖尾阴影过高且翘尾，本数据也不适合采用L型，prob=0.1更适合直线下降或上升，故案例文件最终采用U型曲线图。RCS分析后可为x是否存在非线性关联与型态，及其切点为后续cox分析中x的P-trend，或四分位，或2分类提供分类依据。这里需要注意，本例仅作为数据演示，模拟数据不符合PH假设后续仍然需要进行其他非等比例cox分析，将在V2.0版本补充。

4.2 实战logistic分析

加载rcssci包后，一行命令搞定logistic分析rcs绘制，prob推荐0.1，不写默认0.5。结果解析同cox。

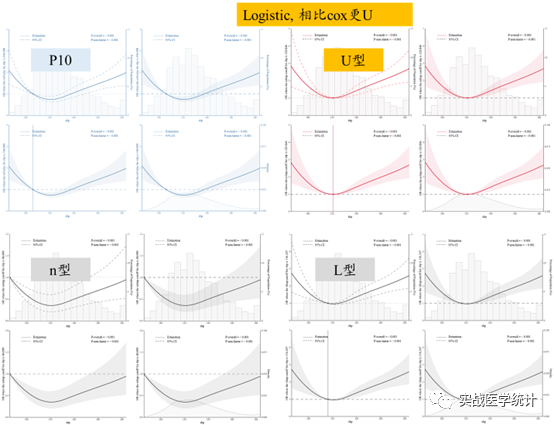
rcssci_logistics(data=sbpdata, y = "status",x = "sbp",covs=c("age","gender"), prob=0.1)

4.3 实战linear分析

加载rcssci包后，一行命令搞定一般线性分析rcs绘制，prob推荐0.1，不写默认0.5。设置结果输出到目录D:/temp/rcssci。

rcssci_linear (data=sbpdata, y = "status",x = "sbp",covs=c("age","gender"), prob=0.1, filepath= “D:/temp/rcssci”)

结果解析：本例研究结果为：P-overall<0.001，P non-linear <0.001，表明总的检验有意义，非线性关联检验也有意义，呈现出平原阈值关联。大致在60岁-80岁，为平原阈值。y为连续型，往往更偏重描述曲线递增或递减趋势。本例从L型断点发现80岁是个断点。

5. 发散思维

5.1 RCS能否证实切点

笔者测试觉得，如果根据最小AIC评价且严格测试K Q，且K在3-4以内，拟合出的曲线较为平滑，是可以证实切点的。当然，如果有时候K太大，例如K=7的AIC最小曲线拟合过度复杂，尤其是小样本研究，此时得到的切点更多是提供线索。Q最好保持默认，也可以选择平均分配，选取剧烈变化的区域，数据变化复杂的地方多设置节点，更稳定的地方少设置节点。

5.2 rms包的ref.zero=T/F 和fun转换

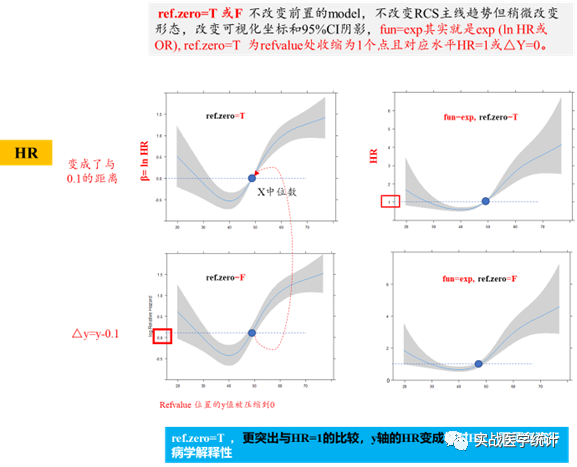
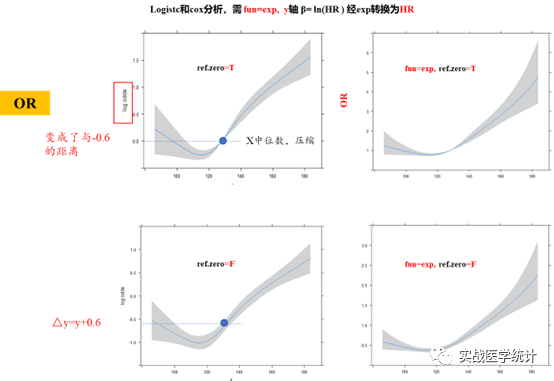
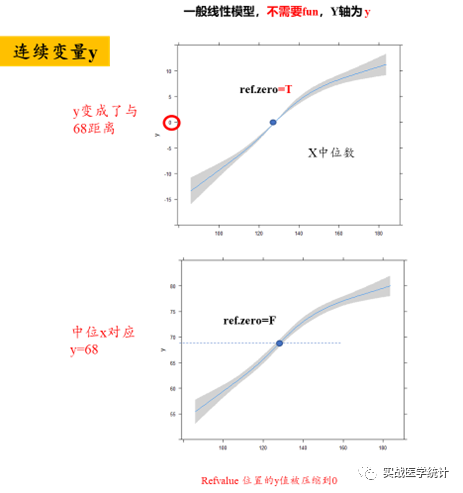
5.3 SCI中的RCS套路

5.4 U型或n型3切点

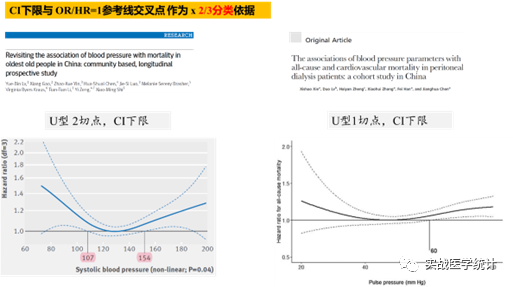
rcssci包V1.0版目前加入的是主流OR/HR/y值，可以探索x值的2分类切点。当需要探索x值3分类切点时，可尝试宽95%CI下限(设置ref.zero=F)与OR/HR=1的参考线交叉处就很可能是3分类的refvalue。当然HR、OR切点寻找方式还有很多，比如ROC曲线、xtile、KM法、GAM法、临床界值（适合组间不均衡）、Tertiles/Quartiles（适合组间均衡）等，能作出阳性结果就是好方法。最后，这些方法其实都是辅助，统计方法的切点有没有临床意义才更加关键，有时候不如直接看看临床界值。

5.5 非线性关联的套路

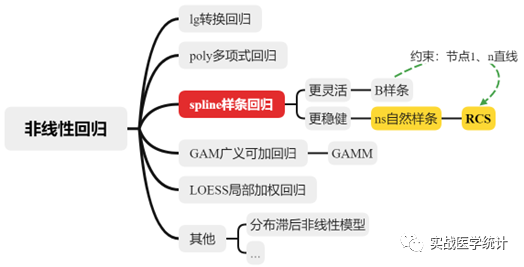
非线性关系常见的解决方法：多项式回归、分段回归。但是多项式回归中，容易共线性、过拟合、全局性等情况；分段回归中类别数目和节点位置的选择带有主观性，分类往往会损失信息，RCS就是目前分析非线性关系的最常见最流行的方法。RCS=限制性(knot约束)立方样条，样条回归本质上其实是一个分段多项式，特别之处是节点knot上连续且二阶可导保证了曲线平滑。更多非线性模型见，https://www.r-bloggers.com/2014/09/an-exercise-in-non-linear-modeling。

6 tips

这是笔者第一次开发R包，开发期间各种bug层出不穷。不过，为了不给小伙伴们添堵，笔者把Hadley Wickham的R packages通篇读了一遍，同时配合包制作了本章RCS攻略。可以负责任拍脑袋的说，是全球最详尽的RCS攻略了。哈哈，英文还没做操作手册呢，所以中文本公众号独享。本文论述的rcssci 包V1.0版为试水之作，第一次安装需要加装Rtools，不足之处或者报错还请加笔者好友私聊。各位小伙伴如果有什么强烈需求，也可在本文下方留言许愿并联系笔者提供你的数据，后续更新没准就会一一实现功能。

参考文献：

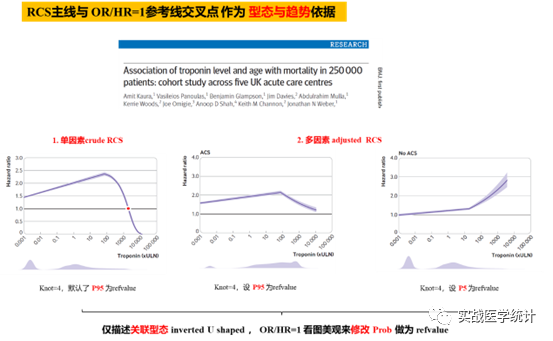
1. Association of troponin level and age with mortality in 250 000 patients: cohort study across five UK acute care centres. BMJ. 2020;369:m2225. Published 2020 Jun 18. doi:10.1136/bmj.m2225

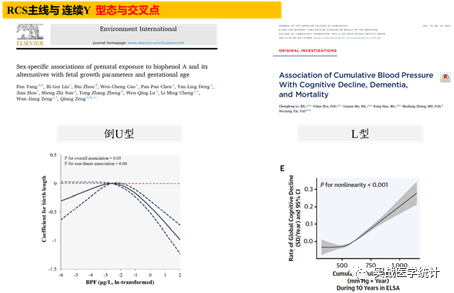
2. Lv YB, Gao X, Yin ZX, et al. Revisiting the association of blood pressure with mortality in oldest old people in China: community based, longitudinal prospective study. BMJ. 2018;361:k2158. Published 2018 Jun 5. doi:10.1136/bmj.k2158

3. https://www.nature.com/articles/s43587-022-00201-3

4. Hu X, Nie Z, Ou Y, et al. Air quality improvement and cognitive function benefit: Insight from clean air action in China. Environ Res. 2022;214(Pt 4):114200. doi:10.1016/j.envres.2022.114200

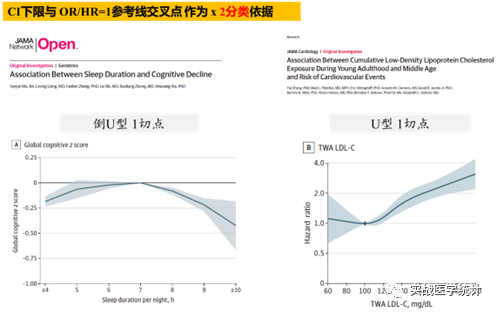
5. Ma Y, Liang L, Zheng F, Shi L, Zhong B, Xie W. Association Between Sleep Duration and Cognitive Decline. JAMA Netw Open. 2020;3(9):e2013573. Published 2020 Sep 1. doi:10.1001/jamanetworkopen.2020.13573