当前位置：首页 > article >正文

备战春招——12.2算法

article 2024/11/17 7:24:47

动态规划

动态规划的核心思想就是本次只由上一次决定。不递归连贯考虑。

判断子序列

还不会，好像是先遍历了一遍数据，用一个动态规划，从改点后下一个位置。

费波拉斯数列

在这里插入图片描述
费波拉斯数列嘛。

class Solution {
public:
    int fib(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        int  a = 0;
        int  b = 1;
        int sum = 0;
        for(int i=2;i<=n;i++){
            sum=a+b;   f(x) = f(x-1)+f(x-2);
            a= b ;      //更新下一个f(x-2)
            b =sum;     //更新下一个f(x-1)
        }
        return sum;
    }
};

使用最小花费爬楼梯

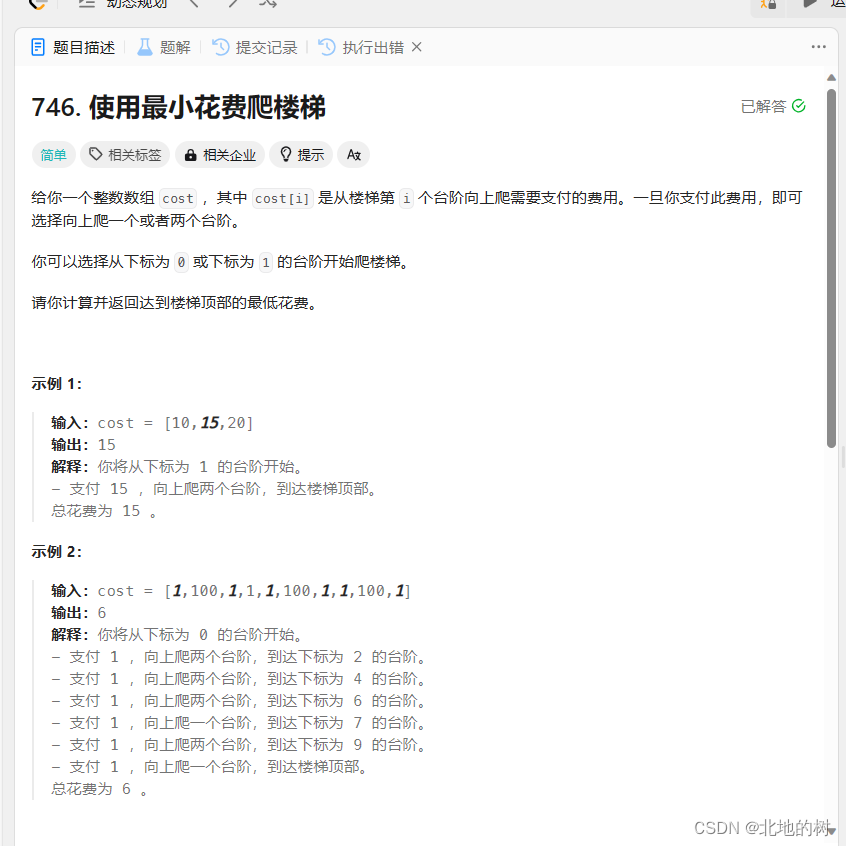
在这里插入图片描述
cost[cost.size()]是顶层，因此是从0索引的，对高楼梯、楼梯时cost[n-1].

dp[i] = min(dp[i-1]+cost[i-1],dp[i-1]+cost[i-2])

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        // 动态规划不一定是规划直接变量，例如cost
        //这里动态动画最小数量。
        int n = cost.size();
        vector<int> dp(n+1,0);
         //最小花费dp     dp[i] = min(dp[i-1]+cost[i-1],dp[i-1]+cost[i-2])
        
        dp[0] = 0;
        dp[1] = 0;
        for(int i=2;i<=cost.size();i++){    //cost.size()就是顶层哈，因为索引的时候是cost[n-1],所以是对的
            dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);  
        }  
        return dp[n];
    }
};

除数博弈

在这里插入图片描述

emm，这题咋这么尴尬，这个动态规划，还没看懂，哎

class Solution {
public:
    bool divisorGame(int n) {
       //贪心 动态规划  都是最优的话，哪应该是取最大的那个数字。

       
        return n%2==0;
    }
};

第 N 个泰波那契数

在这里插入图片描述
那个公式

class Solution {
public:
    int tribonacci(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        if(n==2) return 1;
        int  f0 = 0;
        int  f1 = 1;
        int  f2 = 1;
        int sum = 0;
        // Tn+3 = Tn + Tn+1 + Tn+2
        for(int i=3;i<=n;i++){
            sum = f0+f1+f2;
            f0 = f1;
            f1 = f2;
            f2 = sum;
        }
        return sum;
    }
};

获取生成数组中最大值

在这里插入图片描述
转换公式

class Solution {
public:
    int getMaximumGenerated(int n) {
        if(n==0) return 0;
        if(n==1) return 1;
        //转换公式
        vector<int> dp(n+1,0);
        dp[0] = 0;
        dp[1] = 1;
        int m  = 0;
        for(int i=2;i<=n;i++){
            if(i%2==0) dp[i] = dp[i/2];
            else dp[i] = dp[(i-1)/2+1]+dp[(i-1)/2];
            if(m<dp[i]) m = dp[i];  
        }
        return m;
    }
};