基于c++版本的数据结构改-python栈和队列思维总结
##栈部分-(叠猫猫)
##抽象数据类型栈的定义:是一种遵循先入后出的逻辑的线性数据结构。
换种方式去理解这种数据结构如果我们在一摞盘子中取到下面的盘子,我们首先要把最上面的盘子依次拿走,才可以继续拿下面的盘子,我们把盘子替代成各种类型的元素(如整形,字符,对象等),对于栈就是类似这种衍生出来的线性数据结构。

##栈的定义(c++):是限定仅在表尾进行插入或删除操作的线性表
##图例介绍
##LIFO结构:
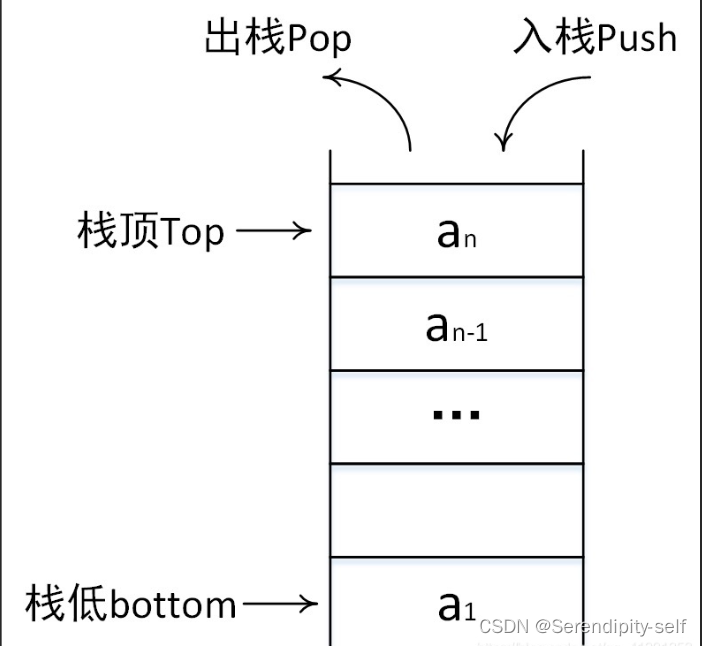
##动态过程

##栈的表示和实现
##栈常用操作:pop(),push(),peek()

然而,某些语言可能没有专门提供栈类,这时我们可以将该语言的“数组”或“链表”当作栈来使用,并在程序逻辑上忽略与栈无关的操作。
栈遵循先入后出的原则,我们只能在栈顶添加或删除元素。
但是,数组和链表都可以在任意位置添加和删除元素,所以栈可以看作是一种受限制的数组或链表。
##栈的顺序表示-基于数组的实现
采用具有一块连续存储的地址进行相关操作,具有代表性的便是数组,基于数组的实现栈。
我们可以将数组的尾部视作栈顶,入栈和出栈操作分别对应在数组的尾部添加或者删除元素,时间复杂度都为O(1)。
##图解

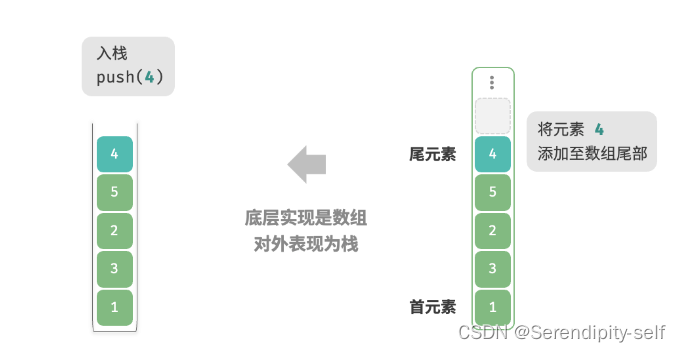

##python代码实现
考虑到入栈的元素可能会远远不断的地增加,因此我们可以使用动态数组,这样就可以不用自行处理数组的扩容问题。
在进行代码介绍之前,我们先介绍一下Python中类class基础篇(用简单的话来说,类是一个模板,而实例则是根据类创建的对象)
##Python类的定义与实例的创建
类的创建-类通过 class 关键字定义,类名通用习惯为首字母大写
class Circle(object):#创建Circle类,Circle为类名
pass#此处可添加属性和方法
实例的创建-创建实例使用 类名+(),类似函数调用的形式创建。
circle1 = Circle()
circle = Circle()
##Python类中的实例属性与类属性
实例属性:用于区分不同的实例
类属性:是每个实例的共有属性
区别:实例属性每个实例都各自拥有,相互独立;而类属性有且只有一份,是共有的属性。
circle1.r = 1#r为实例属性
circle2.R= 2
print(circle.r)#使用 实例名,属性名,可以访问我们的属性
print(circle.R)
在定义 Circle 类时,可以为 Circle 类添加一个特殊的 __init__() 方法,当创建实例时,__init__() 方法被自动调用为创建的实例增加实例属性。
class Circle(object): # 创建Circle类 def __init__(self, r): # 初始化一个属性r(不要忘记self参数,他是类下面所有方法必须的参数) self.r = r # 表示给我们将要创建的实例赋予属性r赋值
class Circle(object): # 创建Circle类
def __init__(self, R): # 约定成俗这里应该使用r,它与self.r中的r同名
self.r = R
circle1 = Circle(1)
print(circle1.r) #我们访问的是小写r类属性-实例属性每个实例各自拥有,互相独立,而类属性有且只有一份。
class Circle(object): pi = 3.14 # 类属性 def __init__(self, r): self.r = r circle1 = Circle(1) circle2 = Circle(2) print('----未修改前-----') print('pi=\t', Circle.pi) print('circle1.pi=\t', circle1.pi) # 3.14 print('circle2.pi=\t', circle2.pi) # 3.14 print('----通过类名修改后-----') Circle.pi = 3.14159 # 通过类名修改类属性,所有实例的类属性被改变 print('pi=\t', Circle.pi) # 3.14159 print('circle1.pi=\t', circle1.pi) # 3.14159 print('circle2.pi=\t', circle2.pi) # 3.14159 print('----通过circle1实例名修改后-----') circle1.pi=3.14111 # 实际上这里是给circle1创建了一个与类属性同名的实例属性 print('pi=\t', Circle.pi) # 3.14159 print('circle1.pi=\t', circle1.pi) # 实例属性的访问优先级比类属性高,所以是3.14111 print('circle2.pi=\t', circle2.pi) # 3.14159 print('----删除circle1实例属性pi-----')----未修改前----- pi= 3.14 circle1.pi= 3.14 circle2.pi= 3.14 ----通过类名修改后----- pi= 3.14159 circle1.pi= 3.14159 circle2.pi= 3.14159 ----通过circle1实例名修改后----- pi= 3.14159 circle1.pi= 3.14111 circle2.pi= 3.14159实例属性访问优先级比类属性高
##Python类的实例方法
class Circle(object): pi = 3.14 # 类属性 def __init__(self, r): self.r = r # 实例属性 def get_area(self): """ 圆的面积 """ # return self.r**2 * Circle.pi # 通过实例修改pi的值对面积无影响,这个pi为类属性的值 return self.r**2 * self.pi # 通过实例修改pi的值对面积我们圆的面积就会改变 circle1 = Circle(1) print(circle1.get_area()) # 调用方法 self不需要传入参数,不要忘记方法后的括号 输出 3.14
##基于数组栈的代码实现
class ArrayStack:
"""基于数组实现额栈"""
def __init__(self):
"""构造方法"""
self._stack:list[int] = []
def size(self):
"""获取栈的长度"""
return len(self._stack)
def is_empty(self):
"""判断栈是否为空"""
return self._stack == []
def push(self,item):
"""入栈"""
self._stack.append(item)
def pop(self):
"""出栈"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack.pop()
def peek(self):
"""访问栈顶元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._stack[-1]
def to_list(self):
"""返回列表用于打印"""
return self._stack时间效率:在基于数组的实现中,入栈和出栈操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入栈时超出数组容量,会触发扩容机制,导致该次入栈操作的时间复杂度变为O(n) 。
空间效率:在初始化列表时,系统会为列表分配“初始容量”,该容量可能超出实际需求;并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容的,扩容后的容量也可能超出实际需求。因此,基于数组实现的栈可能造成一定的空间浪费。
##栈的链式表示
使用链表实现栈时,我们可以将链表的头结点视为栈顶,尾结点视为栈底。
在进行插入元素的时候我们只需要把结点插入链表的头部,这种方法被称为“头插法”。
在进行删除操作时只需要把头结点删除即可。
##链栈示意图

##图解


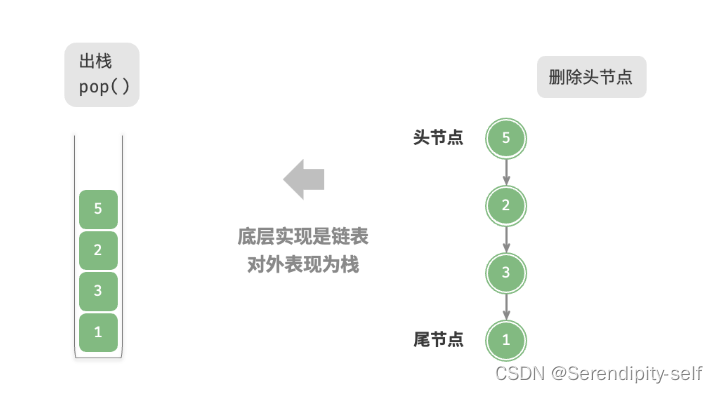
##Python链栈代码实现
class ListNode(object):
"""定义链表"""
def __init__(self):
self.val = None
self.next = None
class LinkedListStack:
"""基于链表实现的栈"""
def __init__(self):
"""构造方法"""
self._peek:ListNode | None = None
self._size: int = 0
def size(self):
"""获取栈的长度"""
return self._size
def is_empty(self):
"""判断栈是否为空"""
return self._size
def push(self,val):
"""入栈"""
node = ListNode(val)
node.next = self._peek
self._peek = node
self._size += 1
def pop(self):
"""出栈"""
if self.is_empty():
raise IndexError("栈为空")
return self._peek.val
def to_list(self):
"""转化为列表用于打印"""
arr = []
node = self._peek
while node :
arr.append(node.val)
node = node.next
arr.reverse()
return arr时间效率:在基于链表的实现中,链表的扩容非常灵活,不存在上述数组扩容时效率降低的问题。但是,入栈操作需要初始化节点对象并修改指针,因此效率相对较低。不过,如果入栈元素本身就是节点对象,那么可以省去初始化步骤,从而提高效率。
空间效率:由于链表节点需要额外存储指针,因此链表节点占用的空间相对较大。
##栈典型的用例
浏览器中的后退与前进、软件中的撤销与反撤销。每当我们打开新的网页,浏览器就会对上一个网页执行入栈,这样我们就可以通过后退操作回到上一个网页。后退操作实际上是在执行出栈。如果要同时支持后退和前进,那么需要两个栈来配合实现。
程序内存管理。每次调用函数时,系统都会在栈顶添加一个栈帧,用于记录函数的上下文信息。在递归函数中,向下递推阶段会不断执行入栈操作,而向上回溯阶段则会不断执行出栈操作。
##队列部分-猫猫排队
是一种遵循先入先出规则的线性数据结构。
是一种模拟排队现象,新来的人不断加入到队列尾部,而位于队列头部的人不断离开。

##抽象数据类型队列的定义
队列是一种先进先出的线性表,它只允许在表的一端进行插入,而在另一端删除元素。
##图例显示

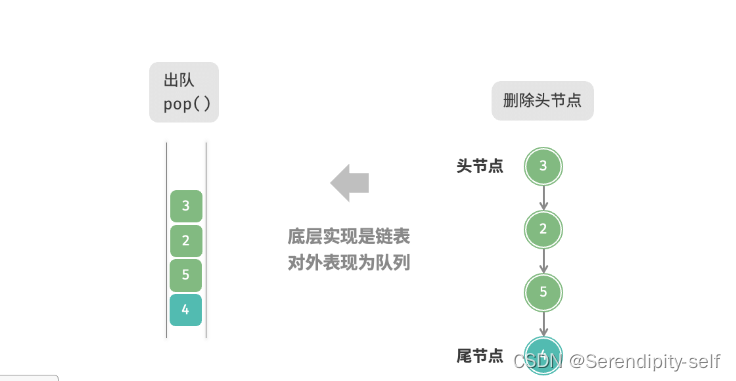
我们将队列头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。

##队列的常用操作
 ##图解
##图解


##基于数组的队列实现
我们在数组中进行删除首元素的时间复杂度为O(n),这就导致了出队的操作效率低下。
采用变量front指向队首元素的索引,rear = front + size ,通过一个变量size来记录队列的长度。
基于此设计,数组中所包含的元素的有效区间为[front,rear - 1]。

入队操作:只需要将元素赋值给rear索引处,并将size增加1。

出队操作:只需要将front增加1,并将size减少1。

##问题:
在不断进行入队和出队的过程中,front 和 rear 都在向右移动,当它们到达数组尾部时就无法继续移动了。为了解决此问题,我们可以将数组视为首尾相接的“环形数组”。
对于环形数组,我们需要让 front 或 rear 在越过数组尾部时,直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现,
##基于数组的队列代码实现
class ArrayQueue:
"""基于环形数组实现的队列"""
def __init__(self,size):
"""构造方法"""
self._nums : list[int] = [0] *size #用于存储队列元素的数组
self._front : int = 0 #队首指针,指向队首元素
self._size : int = 0 #队列长度
def capacity(self):
"""获取队列的容量"""
return len(self._nums)
def size(self):
"""获取队列的长度"""
return self._size
def is_empty(self):
"""判断队列是否为空"""
return self._size == 0
def push(self,num):
"""入队操作"""
if self._size == self.capacity():
raise IndexError("队列已满")
#计算尾指针,指向对尾的索引 + 1
#通过取余操作,实现rear超过数组尾部后回到头部
rear : int = (self._front + self._size) % self.capacity()
#将num添加至对尾
self._nums[rear] = num
self._size += 1
def pop(self):
"""出队"""
num : int = self.peek()
#队首指针指向后移动一位,若超过数组尾部后回到头部
rear : int = (self._front + self._size) % self.capacity()
self._size -= 1
return num
def peek(self):
"""访问队首元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._nums[self._front]
def to_list(self):
"""转化成列表用于打印"""
res = [0] * self.size()
j : int = self._front
for i in range(self.size()):
res[i] = self._nums[(j%self.capacity())]
j += 1
return res时间效率:在基于数组的实现中,入对和出对操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入对时超出数组容量,会触发扩容机制,导致该次入对操作的时间复杂度变为O(n) 。
空间效率:在初始化列表时,系统会为列表分配“初始容量”,该容量可能超出实际需求;并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容的,扩容后的容量也可能超出实际需求。因此,基于数组实现的栈可能造成一定的空间浪费。
##基于链表的队列实现
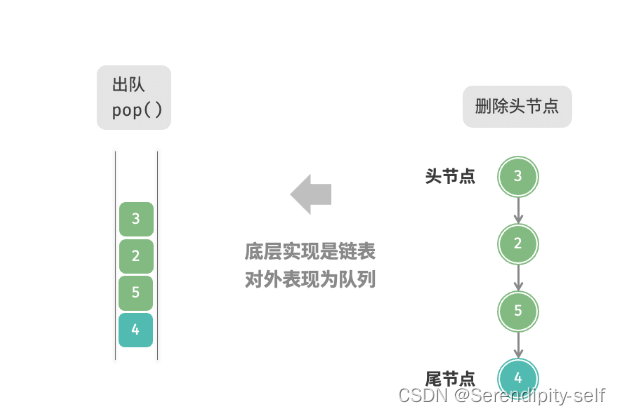
可以将链表的“头节点”和“尾节点”分别视为“队首”和“队尾”,规定队尾仅可添加节点,队首仅可删除节点。
##图解


##基于链表的队列实现代码
class ListNode:
"""定义链表"""
def __init__(self):
self.val = None
self.next = None
class LinkedListQueue:
"""基于链表实现的队列"""
def __init__(self):
"""构造方法"""
self._front : ListNode | None = None #头结点front
self._rear: ListNode | None = None # 尾节点 rear
self._size: int = 0
def size(self):
"""获取队列的长度"""
return self._size
def is_empty(self):
"""判断队列是否为空"""
return not self._front
def push(self, num):
"""入队"""
# 尾节点后添加 num
node = ListNode(num)
# 如果队列为空,则令头、尾节点都指向该节点
if self._front is None:
self._front = node
self._rear = node
# 如果队列不为空,则将该节点添加到尾节点后
else:
self._rear.next = node
self._rear = node
self._size += 1
def pop(self) -> int:
"""出队"""
num = self.peek()
# 删除头节点
self._front = self._front.next
self._size -= 1
return num
def peek(self) -> int:
"""访问队首元素"""
if self.is_empty():
raise IndexError("队列为空")
return self._front.val
def to_list(self) -> list[int]:
"""转化为列表用于打印"""
queue = []
temp = self._front
while temp:
queue.append(temp.val)
temp = temp.next
return queue##队列典型应用
淘宝订单。购物者下单后,订单将加入队列中,系统随后会根据顺序处理队列中的订单。在双十一期间,短时间内会产生海量订单,高并发成为工程师们需要重点攻克的问题。
各类待办事项。任何需要实现“先来后到”功能的场景,例如打印机的任务队列、餐厅的出餐队列等,队列在这些场景中可以有效地维护处理顺序。
