当前位置：首页 > article >正文

二叉树的右视图[中等]

article 2024/9/23 7:23:59

优质博文：IT-BLOG-CN

一、题目

给定一个二叉树的根节点root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

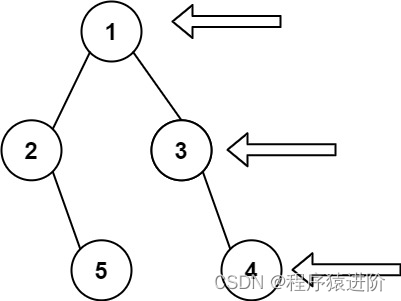
示例 1:
输入: [1,2,3,null,5,null,4]
输出: [1,3,4]

示例 2:
输入: [1,null,3]
输出: [1,3]

示例 3:
输入: []
输出: []

二叉树的节点个数的范围是[0,100]
-100 <= Node.val <= 100

二、代码

由于树的形状无法提前知晓，不可能设计出优于O(n)的算法。因此，我们应该试着寻找线性时间解。带着这个想法，我们来考虑一些同等有效的方案。

【1】深度优先搜索： 我们对树进行深度优先搜索，在搜索过程中，我们总是先访问右子树。那么对于每一层来说，我们在这层见到的第一个结点一定是最右边的结点。这样一来，我们可以存储在每个深度访问的第一个结点，一旦我们知道了树的层数，就可以得到最终的结果数组。

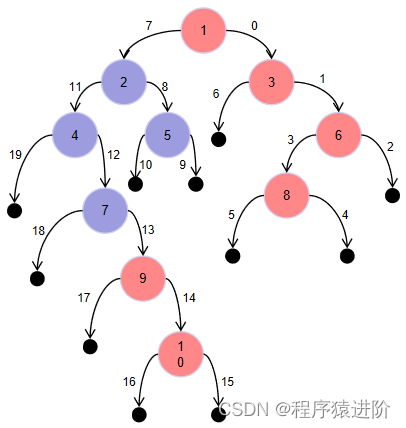
上图表示了问题的一个实例。红色结点自上而下组成答案，边缘以访问顺序标号。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
        int max_depth = -1;

        Deque<TreeNode> nodeStack = new LinkedList<TreeNode>();
        Deque<Integer> depthStack = new LinkedList<Integer>();
        nodeStack.push(root);
        depthStack.push(0);

        while (!nodeStack.isEmpty()) {
            TreeNode node = nodeStack.pop();
            int depth = depthStack.pop();

            if (node != null) {
            	// 维护二叉树的最大深度
                max_depth = Math.max(max_depth, depth);

                // 如果不存在对应深度的节点我们才插入
                if (!rightmostValueAtDepth.containsKey(depth)) {
                    rightmostValueAtDepth.put(depth, node.val);
                }

                nodeStack.push(node.left);
                nodeStack.push(node.right);
                depthStack.push(depth + 1);
                depthStack.push(depth + 1);
            }
        }

        List<Integer> rightView = new ArrayList<Integer>();
        for (int depth = 0; depth <= max_depth; depth++) {
            rightView.add(rightmostValueAtDepth.get(depth));
        }

        return rightView;
    }
}

时间复杂度： O(n)。深度优先搜索最多访问每个结点一次，因此是线性复杂度。
空间复杂度： O(n)。最坏情况下，栈内会包含接近树高度的结点数量，占用O(n)的空间。

【2】广度优先搜索： 我们可以对二叉树进行层次遍历，那么对于每层来说，最右边的结点一定是最后被遍历到的。二叉树的层次遍历可以用广度优先搜索实现。执行广度优先搜索，左结点排在右结点之前，这样，我们对每一层都从左到右访问。因此，只保留每个深度最后访问的结点，我们就可以在遍历完整棵树后得到每个深度最右的结点。除了将栈改成队列，并去除了rightmost_value_at_depth之前的检查外，算法没有别的改动。

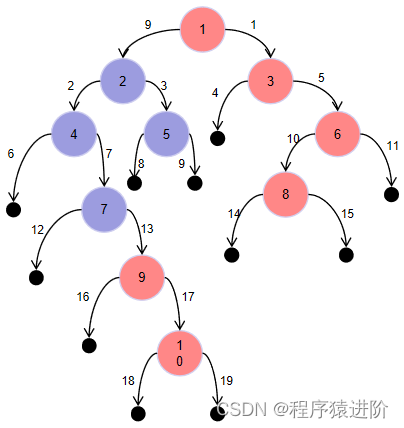
上图表示了同一个示例，红色结点自上而下组成答案，边缘以访问顺序标号。

class Solution {
    public List<Integer> rightSideView(TreeNode root) {
        Map<Integer, Integer> rightmostValueAtDepth = new HashMap<Integer, Integer>();
        int max_depth = -1;

        Queue<TreeNode> nodeQueue = new LinkedList<TreeNode>();
        Queue<Integer> depthQueue = new LinkedList<Integer>();
        nodeQueue.add(root);
        depthQueue.add(0);

        while (!nodeQueue.isEmpty()) {
            TreeNode node = nodeQueue.remove();
            int depth = depthQueue.remove();

            if (node != null) {
            	// 维护二叉树的最大深度
                max_depth = Math.max(max_depth, depth);

                // 由于每一层最后一个访问到的节点才是我们要的答案，因此不断更新对应深度的信息即可
                rightmostValueAtDepth.put(depth, node.val);

                nodeQueue.add(node.left);
                nodeQueue.add(node.right);
                depthQueue.add(depth + 1);
                depthQueue.add(depth + 1);
            }
        }

        List<Integer> rightView = new ArrayList<Integer>();
        for (int depth = 0; depth <= max_depth; depth++) {
            rightView.add(rightmostValueAtDepth.get(depth));
        }

        return rightView;
    }
}