【GAMES101】二维变换和齐次坐标
这几天都在抽空学OpenGL、敲leetcode和看games,这里留点笔记给以后复习
games101第一节课在吹水,第二节课讲了线性代数的入门知识,比较简单,这里稍微回顾一下重点,然后开始讲第三节课的二维变换和齐次坐标
目录
向量
向量的点乘
向量的叉乘
二维变换
缩放
拉伸
旋转
平移
齐次坐标
向量
games101的向量是默认列向量
向量的点乘
向量的点乘就是对应的元素相乘
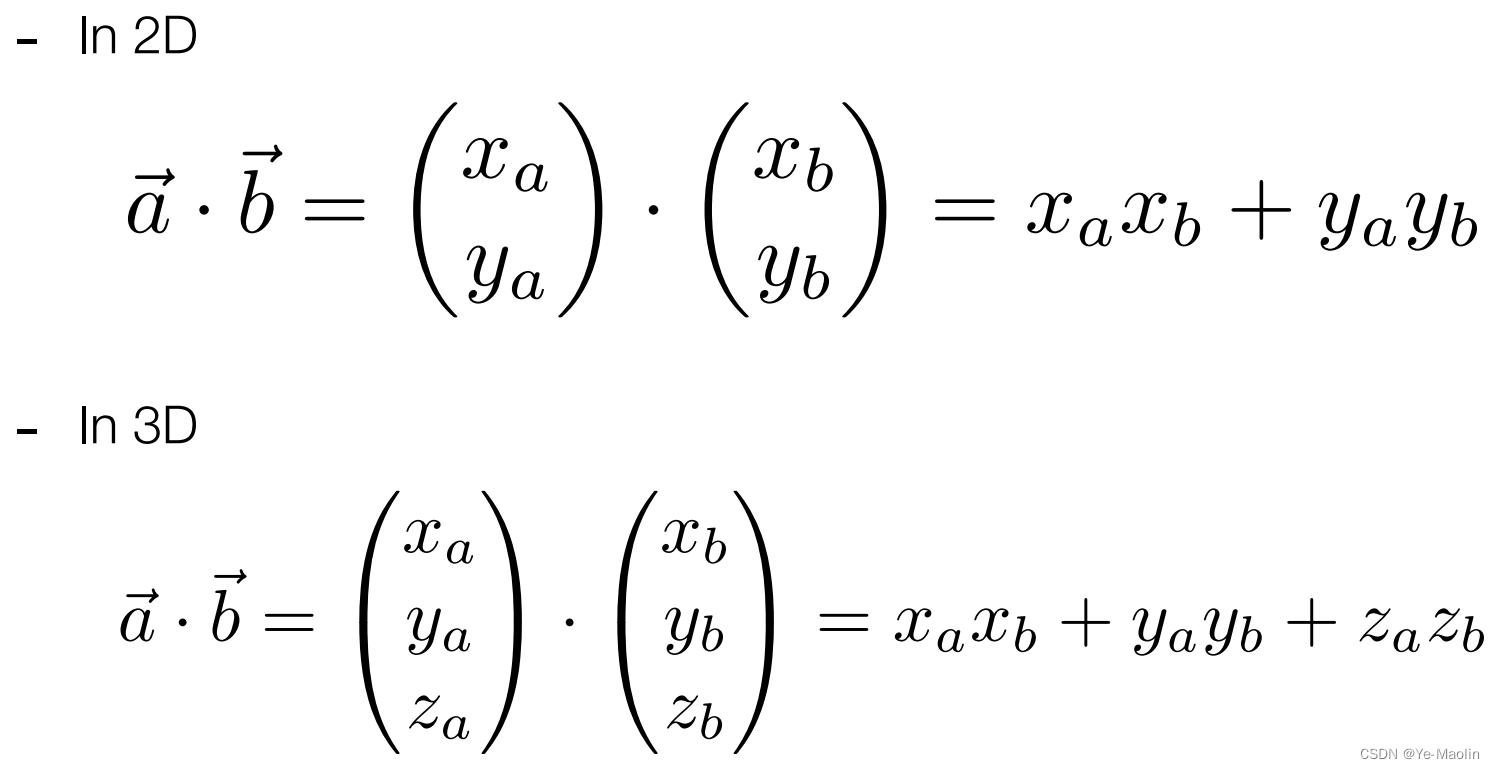
这个可以用来求向量之间的夹角,特别是当两个向量都是单位向量的时候,它们夹角的余弦值就是两个向量点乘的结果
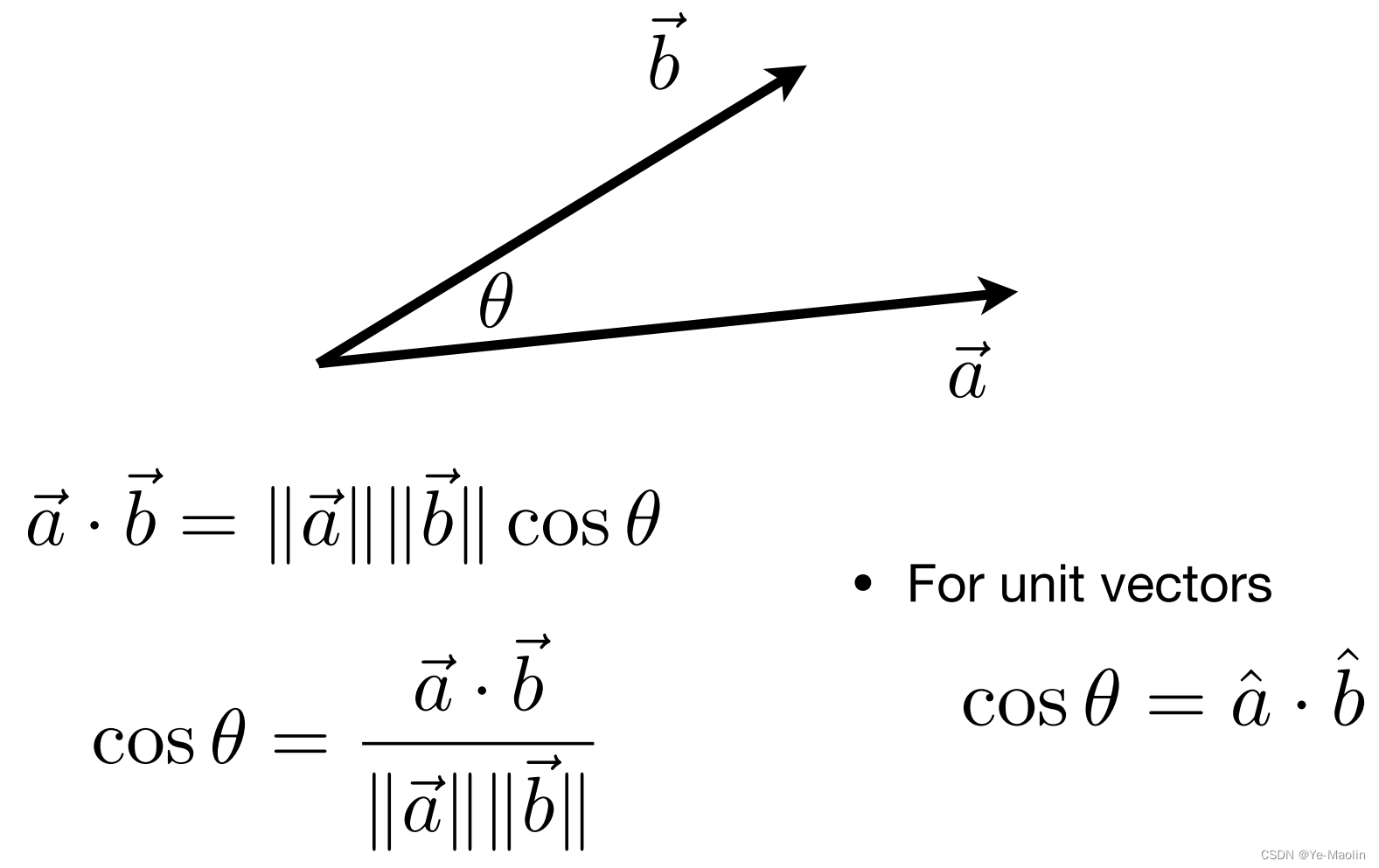
向量的叉乘
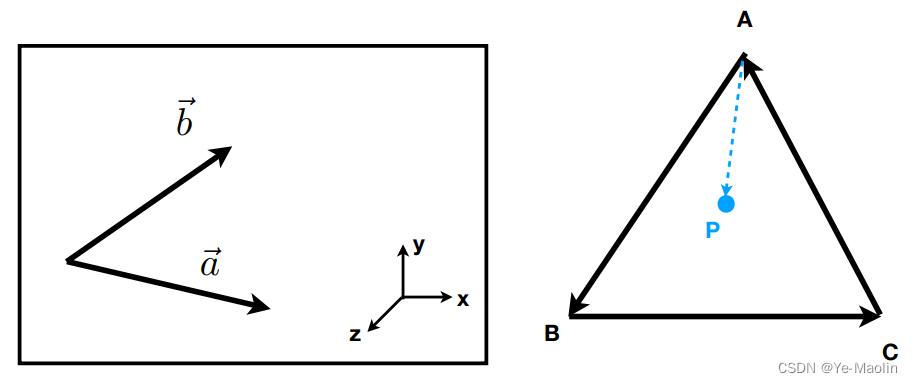
两个向量叉乘的结果是这样的一个向量:方向与两个向量垂直,按右手系是从a旋转到b大拇指指向的方向,大小是两个向量的长度和夹角正弦值的乘积
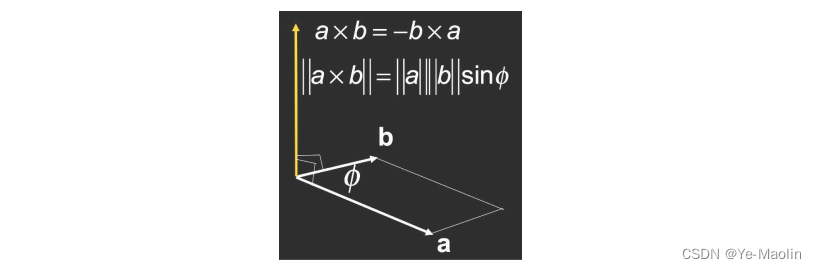
坐标系的话,games101用的是右手系,OpenGL用的也是右手系,但是unity和ue都是左手系
叉乘可以用来判断一个点是否在一个多边形内部,如下P点,如果AP×AB和BP×BC和CP×CA的方向是一样的,那么这个P点就在三角形内部
二维变换
缩放
对于一个图形进行缩放,实际上就是对于每一个点的坐标进行缩放,比如缩小一半,就是x和y都变成原来的一半,这个没有什么问题
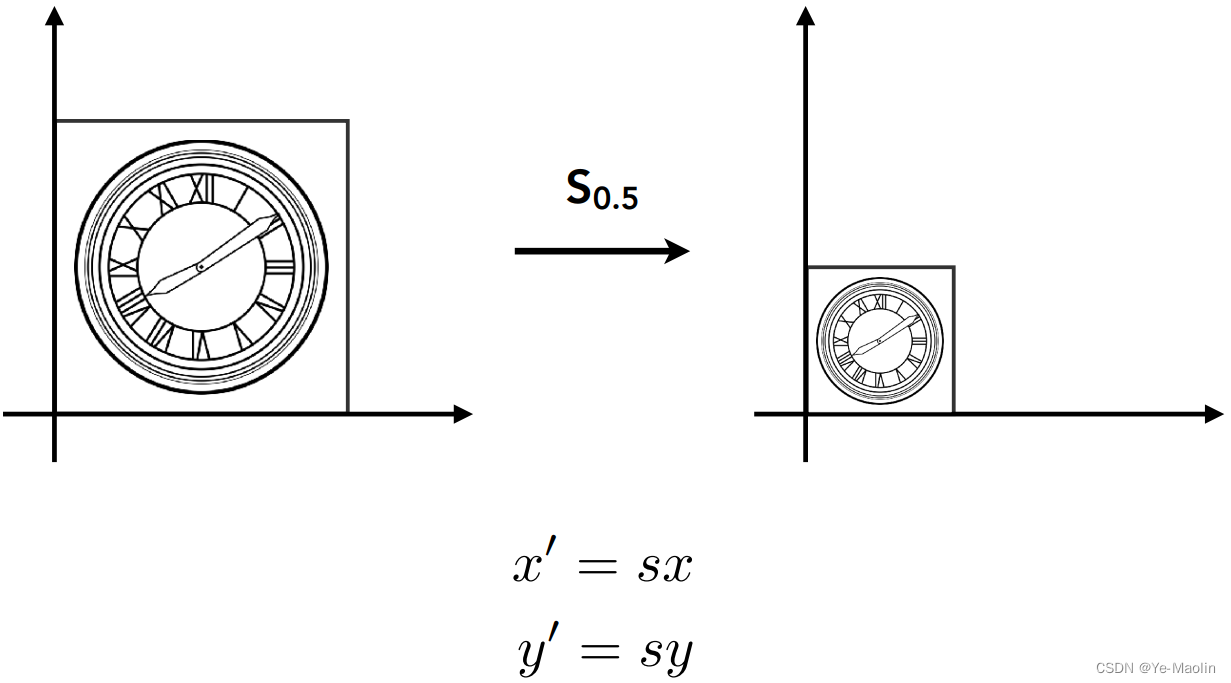
更方便的统一操作,我们可以用一个矩阵乘法来表示缩放这个操作,x和y都乘以s
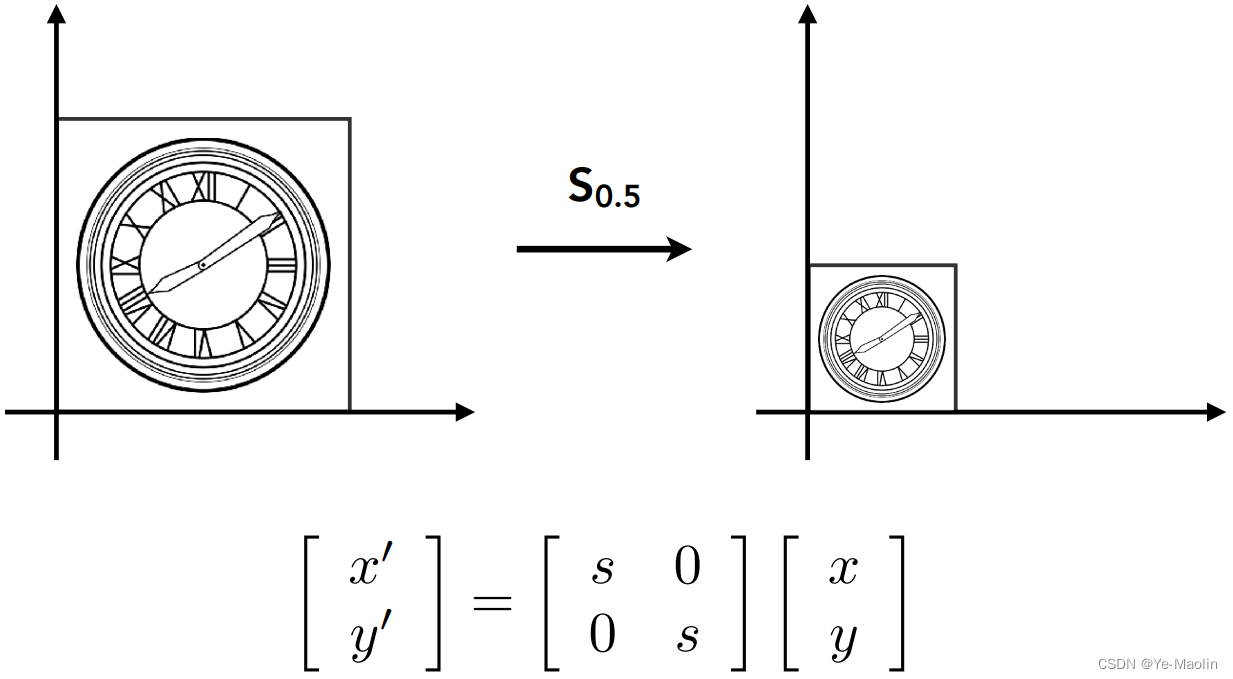
x和y不同程度的拉伸
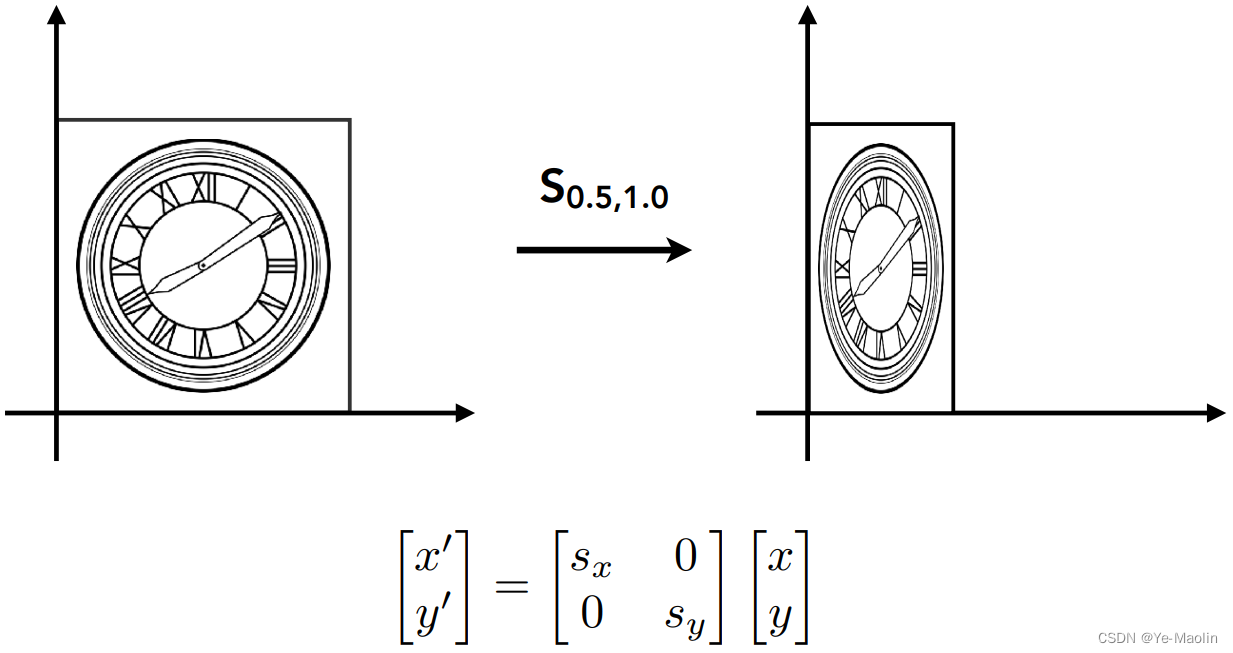
对称变换
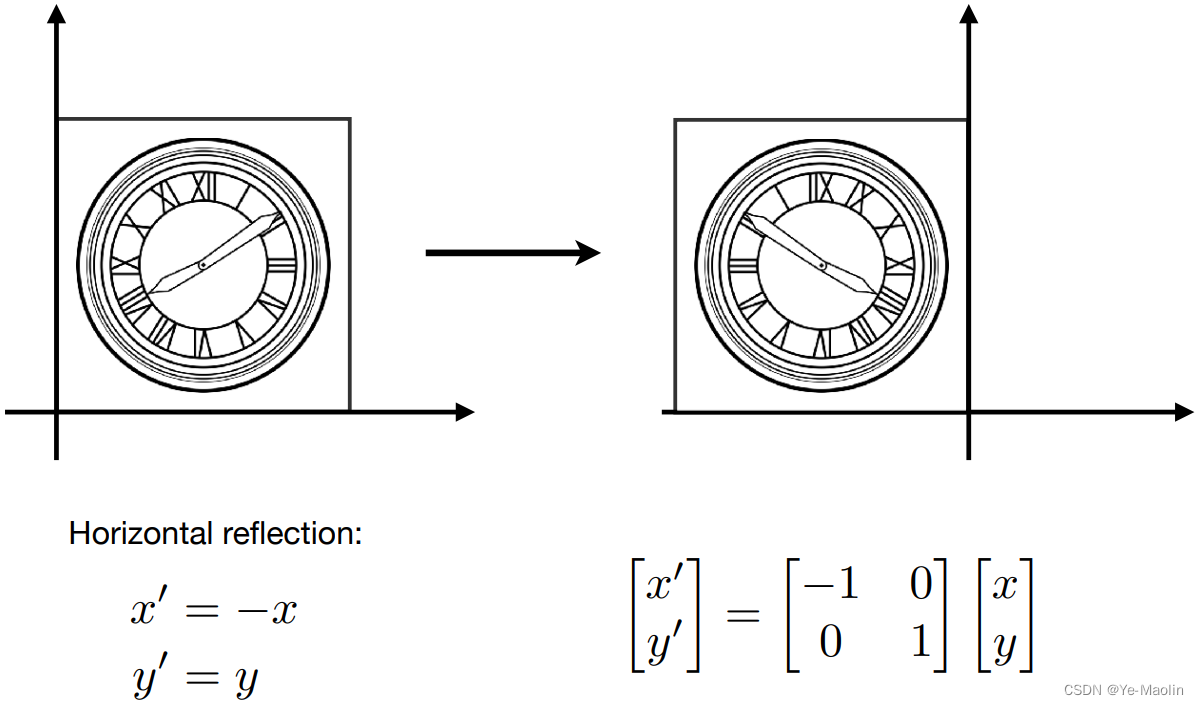
拉伸
往某个方向拉伸,比如x方向,y不变,x’=x+ay
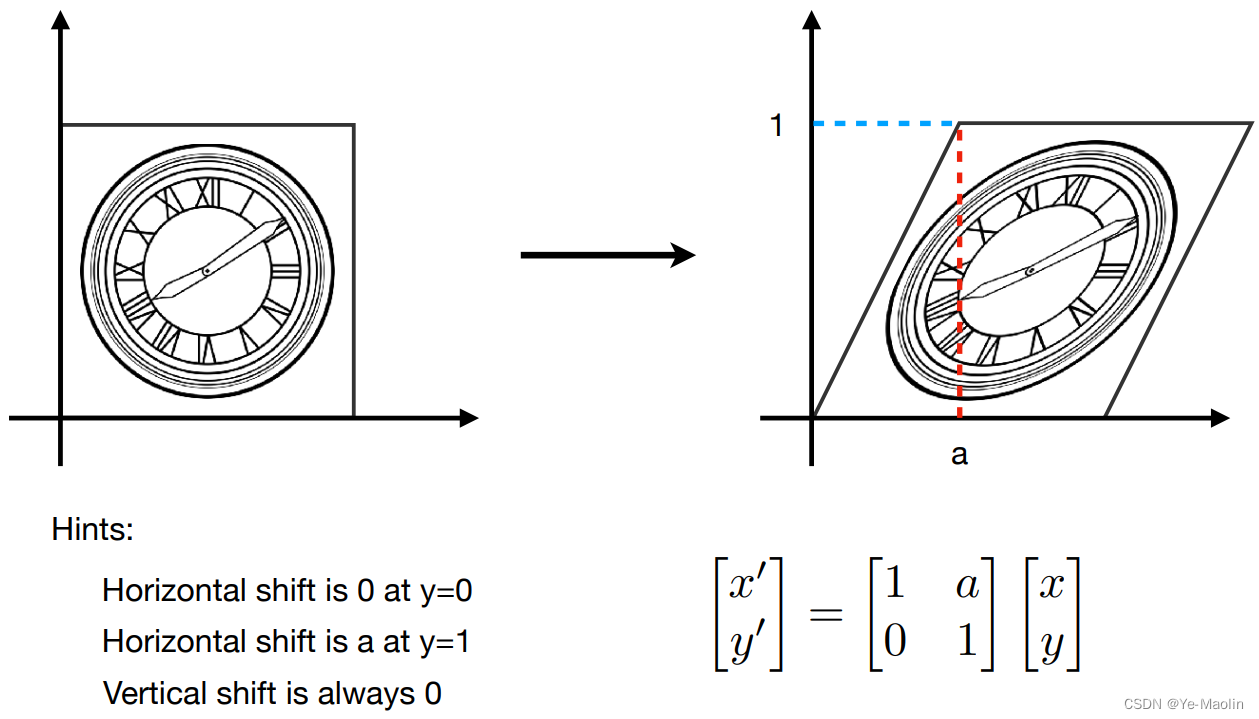
旋转
逆时针旋转,这个可以通过固定两个顶点来推出这个变换矩阵

平移
对于平移,即x和y加上对应的平移量
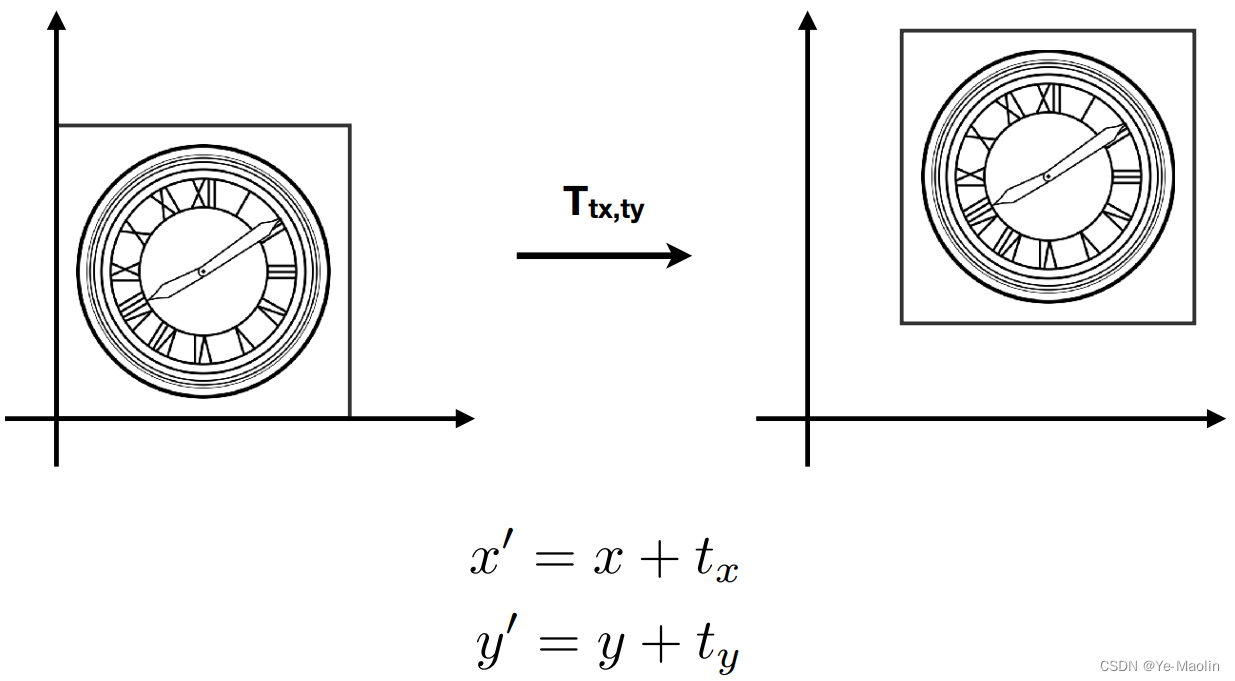
齐次坐标
其实你可能已经发现,在变换中,缩放、拉伸和旋转都可以用一个矩阵乘法来表示,这三个变换又可以称为线性变换,唯独平移不可以用矩阵乘法表示(我尝试过了,真不行)

齐次坐标就是解决这个问题的,可以统一变换为一个矩阵乘法形式
解决办法:通过增加一个维度来表示,第三个维度为1表示这是个点,第三个维度为0表示这是个向量,这样就可以通过三维矩阵乘法来表示平移变换了

这样子的话,那么两个向量相加是向量,两个点相减是向量,一个点加上一个向量还是一个点

那么点加点呢?
实际上还是点,而且是这两个点的中点,因为点,确切的表示是这个:
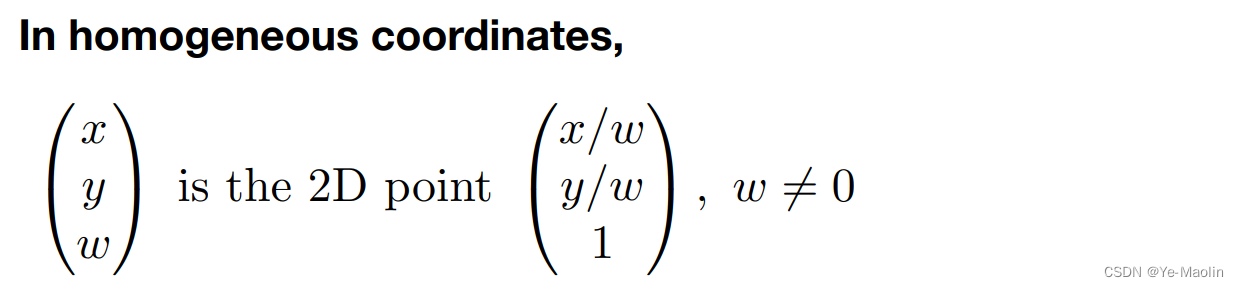
因此通过齐次坐标,我们就可以统一变换为矩阵乘法形式

由于矩阵乘法的规律,所以多次变换是以矩阵左乘的顺序相乘的,而且是先进行线性变换再平移