数据结构之交换排序

目录

交换排序

冒泡排序

冒泡排序的时间复杂度

快速排序

快速排序单趟排序的时间复杂度

快速排序的时间复杂度

交换排序

在日常生活中交换排序的使用场景是很多的，比如在学校做早操，老师通常会让学生按大小个排队，如果此时来了一个新学生，要让他进入队伍，此时就要让他先与队列的第一个学生进行比较，发生交换，最终将他排到合适的队列位置，这就是一个简单的交换排序的使用场景。在数据结构中，我们怎样实现交换排序呢？

 交换排序分为冒泡排序和快速排序（重点），下来就让我们一起研究这两个排序。

冒泡排序

冒泡排序的思想：我们将冒泡排序分成了多个单趟排序，每趟排序找出最大的元素，并且将最大的元素放置于数组的末尾。

冒泡排序的单趟排序代码：

for (int i = 0; i < size -j-1; i++)
		{
			//比较两个元素，因为是排升序，所以如果第一个元素比第二个元素要大，就要发生交换
			if (a[i] > a[i + 1])
			{
				Swap(&a[i], &a[i + 1]);
				flag = 0;
			}
		}

冒泡排序整体代码：

void BubbleSort(int* a, int size)
{
	//整体的排序
	for (int j = 0; j < size - 1; j++)
	{
		//定义一个标志变量，为循环结束的条件
		int flag = 1;
		//单趟排序：先让第一个元素与第二个元素进行比较大小，因为是排升序，所以如果第一个元素比第二个元素大，要发生交换，依此步骤，完成一次单趟排序
		for (int i = 0; i < size -j-1; i++)
		{
			//比较两个元素，因为是排升序，所以如果第一个元素比第二个元素要大，就要发生交换
			if (a[i] > a[i + 1])
			{
				Swap(&a[i], &a[i + 1]);
				flag = 0;
			}
		}
		//优化：如果进行了一趟排序之后，没有元素发生交换，就意味着数组已经变得有序，所以就没有必要再去进行下一趟排序了
		if (flag == 1)
		{
			break;
		}
	}
}

int main()
{
	int arr[] = { 1000,999,888,777,666,555,444,333,222,111 };
	BubbleSort(arr, sizeof(arr) / sizeof(int));
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

 运行截图如下：

 注意：我们里面定义了一个flag变量为循环结束的标志，因为我们对冒泡排序做了优化，因为当一个数组已经有序时，我们人眼可以看出来，但是编译器是看不出来的，所以，我们要设置这个变量，为的就是，当我们进行了一趟排序后，如果没有发生元素的交换，证明此时数组已经变得有序了，所以就没有必要再去进行下一趟排序了，应该直接终止排序，即跳出循环。

冒泡排序的时间复杂度

时间复杂度： 最好：O(N)     最坏：O(N^2)

稳定性：稳定

快速排序

快速排序是排序中最牛也是最重要的排序。 本期我们主要讲解快速排序的递归版本。

快速排序的思想：先进行单趟排序，单趟排序找出key之后，对key左边的数组和key右边的数组依次进行快速排序，按照递归的思想最终完成排序。

单趟排序的思想：

方法一：hoare版本，这个版本是发明快排的大佬所使用的版本，有些难懂，称之为原始版本。

主要思路：1.设置两个变量left和right，分别表示数组第一个元素和最后一个元素的位置，然后规定key为left或者right的位置。

                  2.从left位置开始，找比key位置上的元素大的元素，从right位置开始，找比key位置上的元素小的元素，这里需要注意：如果选取left为key，应从right位置开始找，如果选取right为key，应该从left位置开始找。

                  3.当找到了对应的元素之后，将两个位置上的元素进行交换，分别让left++，right--然后重复上述2步骤，直到left和right处于同一位置，将此位置上的元素与key位置上的元素进行交换，然后将key挪动到此位置，一趟排序就完成了，此时key位置左边的所有位置的元素都比key位置上元素要小，key位置右边的元素都比key位置上的元素都要大，此时就证明key位置上的元素已经放到了最终的位置，排好了序。

单趟排序图示如下：

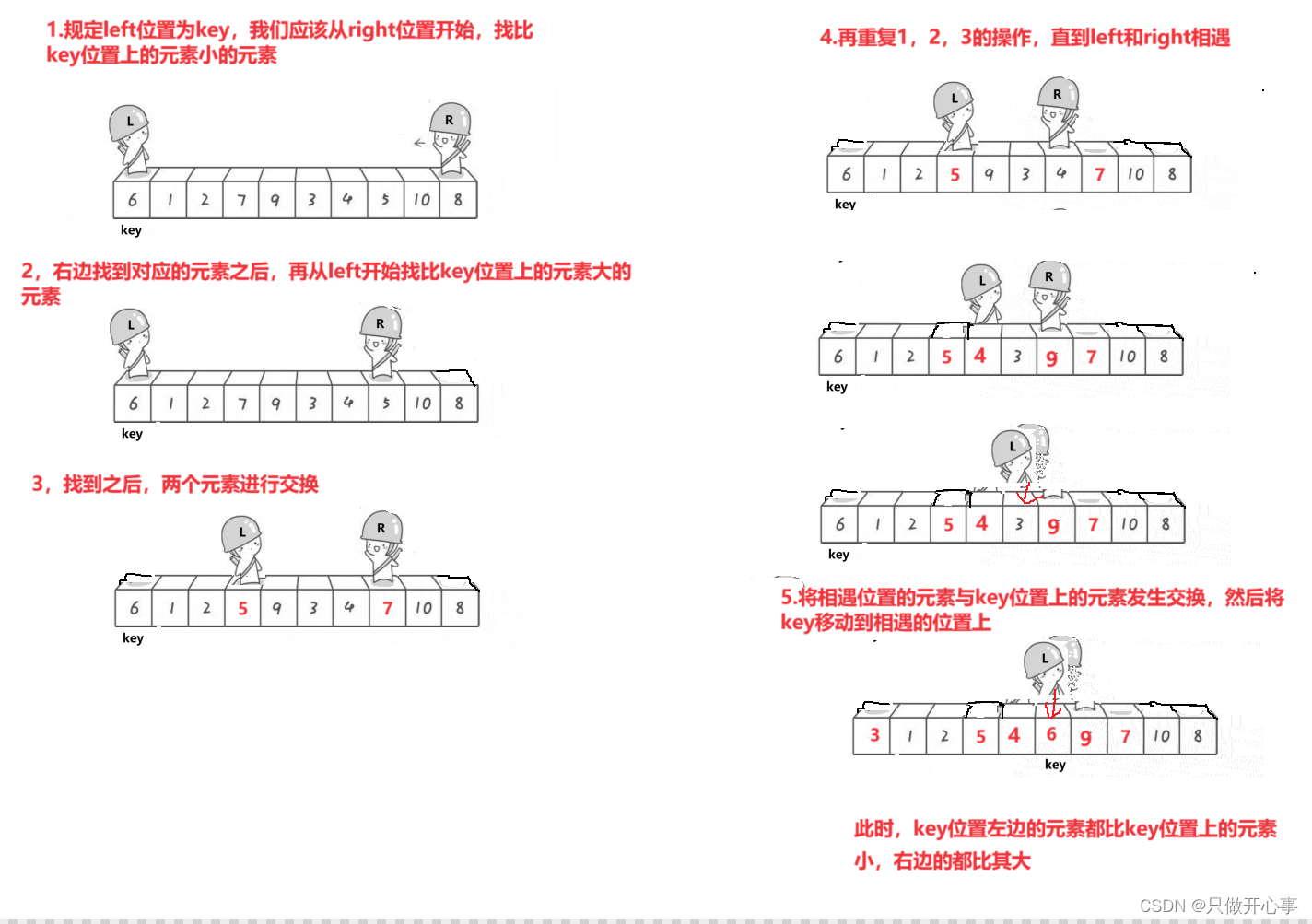
单趟排序的代码如下：

int PartSort1(int* a, int left, int right)
{
	int key = left;
	while (left < right)
	{
		while (left<right && a[right]>=a[key])
		{
			right--;
		}
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		swap(&a[right], &a[left]);
	}
	swap(&a[left], &a[key]);
	key = left;
}

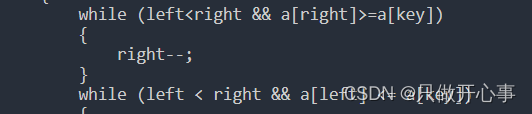
   大家注意这两行代码：

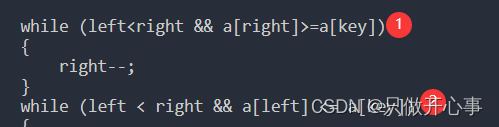
为什么限制条件必须这样写呢？因为我们要避免两种极端情景。

情景1：当数组元素相同时

当数组元素相同时，按照我们以往的算法，从right开始找比key小的，如果比key大就right--，，然后在从left开始找，找比key大的，如果比key小就left++，但是在这种情况下right不可能比key大的，所以right就不可能--，left也不可能比key值小，所以left就不可能++，里面的while循环无法正常进行，所以为了避免这样情况下我们就要，增加判断条件，即a[right]>=a[key]和a[left] <= a[key]，比以往多了一个==，这样就会让left++和right--正常进行。

情景2：当数组已经是个有序数组时：

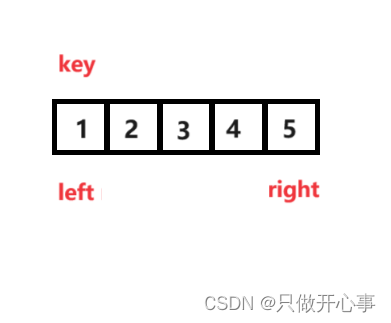
这种情景刚开始都是正常的，但是大家仔细思考下面的两行代码。

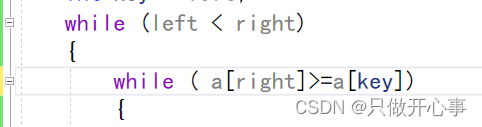
当right和left相遇之后，因为最外层的控制条件只会堆内层的循环产生一次限制影响，所以此时的right仍然会再次--，这就会导致right越界。所以我们还必须加上一个限制条件，里面的while循环也必须加上left<right的限制条件，所以改善之后的代码如下：

单趟排序方法二：挖坑法

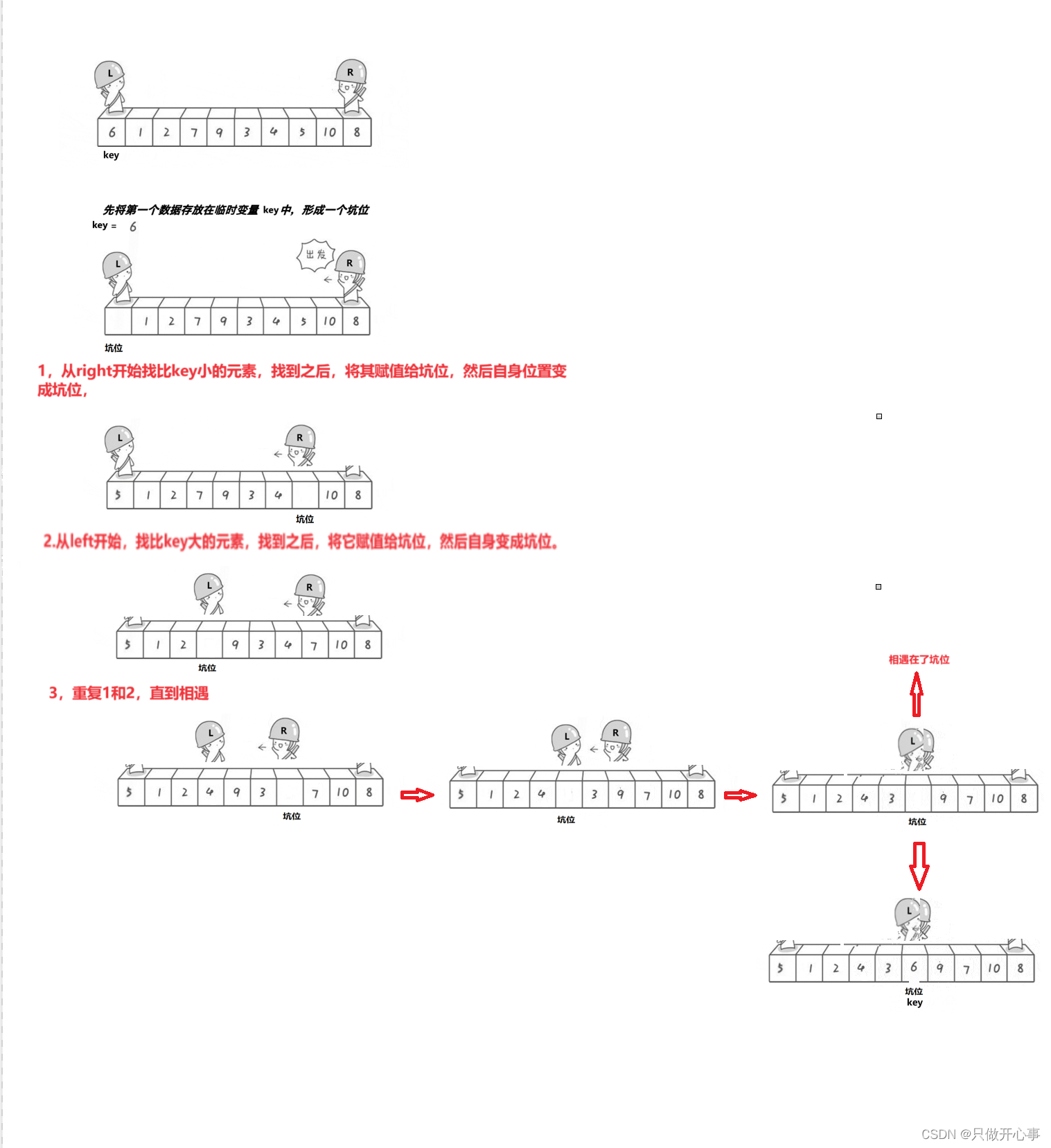
主要思路：1.将第一个数据存放在临时变量key中，然后第一个位置形成一个坑位。然后从right开始找比key小的元素，找到之后与放置到坑位，然后自己成为坑位。

                  2.从left开始找比key大的元素，找到之后放置到坑位，然后自己形成一个坑位。

                  3.重复1,2，直到left和right相遇。最终将key的值放置在坑位，最红key左边的值都小于key的值，右边的值都大于key的值。

单趟排序第二种方法代码：

int PartSort2(int* a, int left,int right)
{
	int mid = GetMid(a, left, right);
	Swap(&a[left], &a[mid]);
	int key = a[left];
	int pivot = left;
	while (left < right)
	{
		while (left<right && a[right]>=key)
		{
			--right;
		}
		a[pivot] = a[right];
		pivot = right;
		while (left < right && a[left] <= key)
		{
			++left;
		}
		a[pivot] = a[left];
		pivot = left;
	}
	a[left] = key;

}

快速排序整体代码：

void  QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	int key= PartSort1(a, left, right);
	QuickSort(a, left, key - 1);
	QuickSort(a, key + 1, right);
}
int main()
{
	int arr[] = { 100,99,88,77,66,55,44,33,22,11 };
	QuickSort(arr,0,sizeof(arr)/sizeof(int)-1);
	for (int i = 0; i < sizeof(arr) / sizeof(int); i++)
	{
		printf("%d ", arr[i]);
	}
	return 0;
}

 运行截图如下：

快速排序单趟排序的时间复杂度

left和right从数组两端一直到相遇，再与key交换，整个过程刚好每个元素都和key位置的元素比较了一次，所以快速排序单趟排序的时间复杂度为O(N)

快速排序的时间复杂度

最好:O(N*logN)

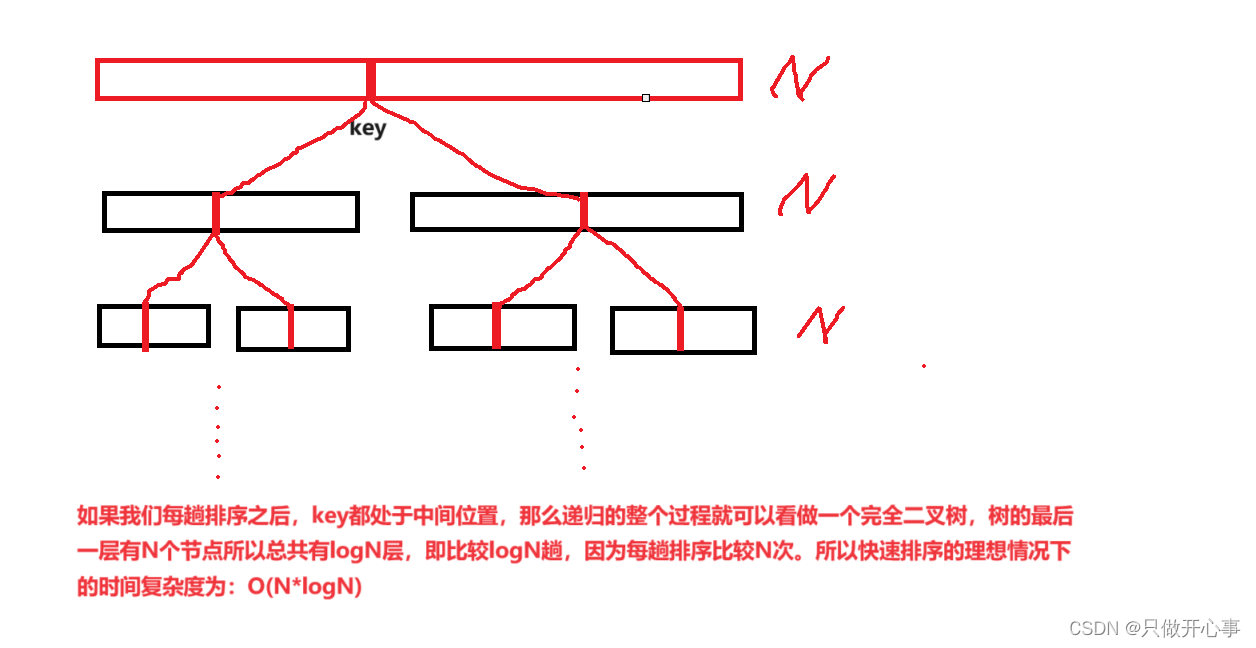
最坏:O(N^2)

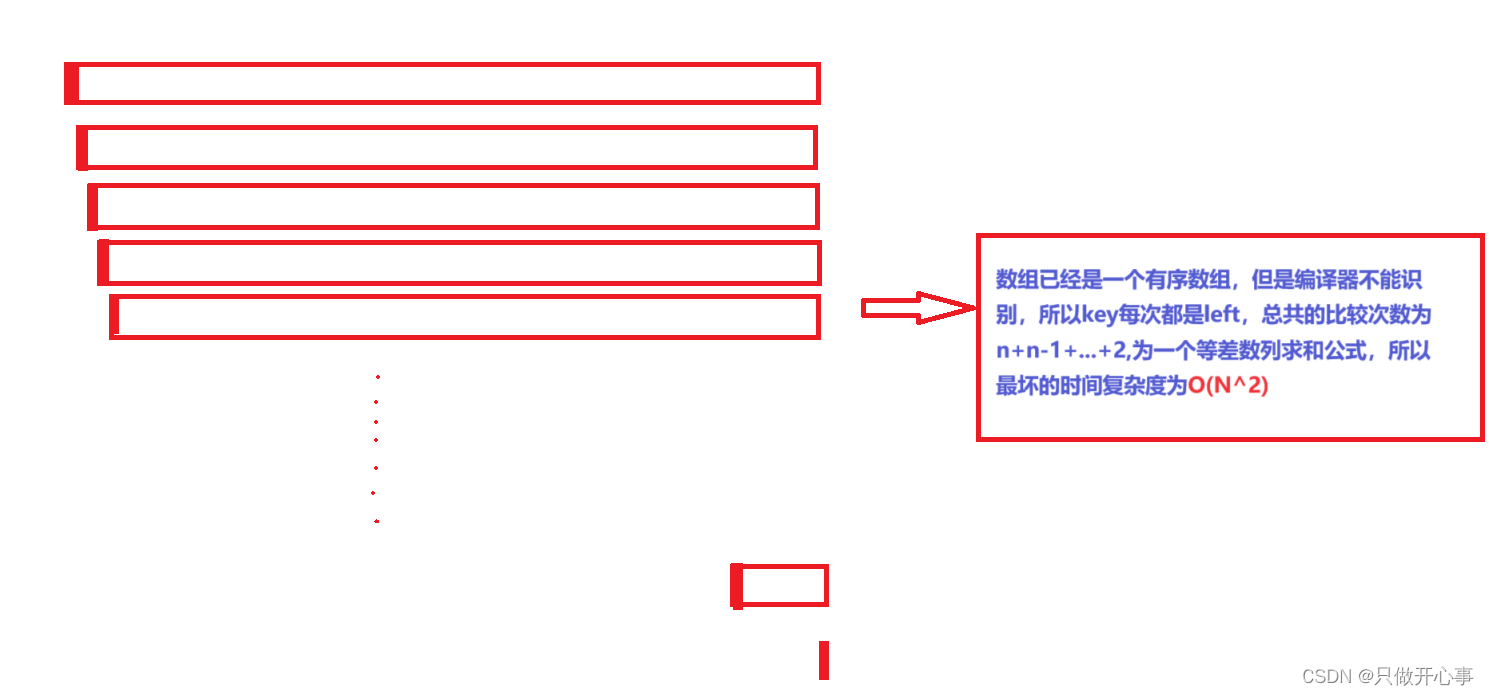
稳定性：不稳定。 

综上我们知道，当数组有序时吗，快排的效率非常差劲，为了提高效率，我们发明了一种三数取中法，为一个将有序数组变称无序数组的方法，以提高效率。

具体思路：在进行单趟排序之前，先将left，right和(left+right)/2,位置上的元素分别进行对比，找出出刚好大小处于中间的元素，将次位置设置成mid；然后将mid位置上的元素与left位置上的元素进行交换，就导致left位置上的元素已经是数组中两个元素中间的一个元素，也就意味着进行了这样的一个调整之后，数组一定是无序的。这样就强制性的改变了快排最坏的情况，向最好的情况引导。

 这就保证了，单趟排序之后，key的位置一定不是处于最边上的位置，而是处于中间的位置。

获取中间元素的位置代码：

int GetMid(int* a, int left, int right)
{
	int mid = left + right / 2;
	if (a[left] < a[mid])
	{
		if (a[mid] < a[right])
			return mid;
		else if (a[left] > a[right])
			return left;
		else
			return right;
	}
	else
	{
		if (a[left] < a[right])
			return left;
		else if (a[mid] > a[right])
			return mid;
		else
			return right;
	}
}

 改进后的单趟排序代码：

int PartSort(int* a, int left, int right)
{
	int mid = GetMid(a, left, right);
	Swap(&a[mid], &a[left]);
	int key = left;
	while (left < right)
	{
		while (left < right && a[right]>=a[key])
		{
			right--;
		}
		while (left < right && a[left] <= a[key])
		{
			left++;
		}
		Swap(&a[right], &a[left]);
	}
	Swap(&a[left], &a[key]);
	key = left;
	return key;
}

 以上便是交换排序的所有内容，比较重要的还得是快速排序，但是快速排序我们只学习了递归版本，非递归版本在下期为大家讲解。欲知后事如何，且看下期分解。

本期的所有内容到此结束^_^