当前位置：首页 > article >正文

LeetCode 2477. 到达首都的最少油耗：深度优先搜索(DFS)

article 2024/9/22 3:48:51

【LetMeFly】2477.到达首都的最少油耗：深度优先搜索(DFS)

力扣题目链接：https://leetcode.cn/problems/minimum-fuel-cost-to-report-to-the-capital/

给你一棵 n 个节点的树（一个无向、连通、无环图），每个节点表示一个城市，编号从 0 到 n - 1 ，且恰好有 n - 1 条路。0 是首都。给你一个二维整数数组 roads ，其中 roads[i] = [a_i, b_i] ，表示城市 a_i 和 b_i 之间有一条 双向路 。

每个城市里有一个代表，他们都要去首都参加一个会议。

每座城市里有一辆车。给你一个整数 seats 表示每辆车里面座位的数目。

城市里的代表可以选择乘坐所在城市的车，或者乘坐其他城市的车。相邻城市之间一辆车的油耗是一升汽油。

请你返回到达首都最少需要多少升汽油。

示例 1：

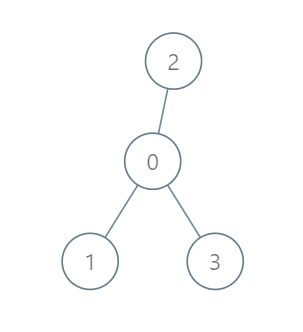
输入：roads = [[0,1],[0,2],[0,3]], seats = 5
输出：3
解释：
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 2 直接到达首都，消耗 1 升汽油。
- 代表 3 直接到达首都，消耗 1 升汽油。
最少消耗 3 升汽油。

示例 2：

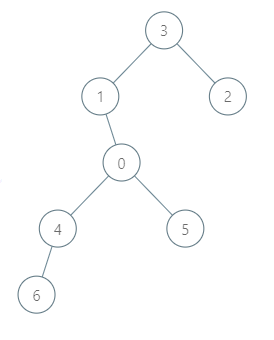
输入：roads = [[3,1],[3,2],[1,0],[0,4],[0,5],[4,6]], seats = 2
输出：7
解释：
- 代表 2 到达城市 3 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达城市 1 ，消耗 1 升汽油。
- 代表 2 和代表 3 一起到达首都，消耗 1 升汽油。
- 代表 1 直接到达首都，消耗 1 升汽油。
- 代表 5 直接到达首都，消耗 1 升汽油。
- 代表 6 到达城市 4 ，消耗 1 升汽油。
- 代表 4 和代表 6 一起到达首都，消耗 1 升汽油。
最少消耗 7 升汽油。

示例 3：

输入：roads = [], seats = 1
输出：0
解释：没有代表需要从别的城市到达首都。

提示：

1 <= n <= 10⁵
roads.length == n - 1
roads[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
roads 表示一棵合法的树。
1 <= seats <= 10⁵

方法一：深度优先搜索(DFS)

车是可以随时“丢弃”与“重选”的，因此我们只需要知道“每一步”有多少人即可。

从“根节点”0开始深搜，深搜过程中，对于节点node：

假设node有数个子节点，各个子节点为根的子树的大小分别为 $a_1$ ， $a_2$ ，…，

那么从这些节点到达节点node分别需要耗油 $\lceil\frac{a_1}{seats}\rceil$ ， $\lceil\frac{a_2}{seats}\rceil$ ，…

将这些耗油累加到答案中，同时也得到了以节点node为根的子树的大小。

上述过程中，所有人一同往根节点的方向走一步，就将耗油累加到了答案中，因此最终返回答案即可。

时间复杂度 $O(N^2)$
空间复杂度 $O(N\log N)$

AC代码

C++

class Solution {
private:
    long long ans;
    vector<vector<int>> graph;
    vector<bool> visited;

    long long dfs(int node, int seats){
        visited[node] = true;
        int cnt = 1;
        for (int toNode  : graph[node]) {
            if (!visited[toNode]) {
                long long peopleFromThatNode = dfs(toNode, seats);
                cnt += peopleFromThatNode;
                ans += (peopleFromThatNode + seats - 1) / seats;
            }
        }
        return cnt;
    }

public:
    long long minimumFuelCost(vector<vector<int>>& roads, int seats) {
        ans = 0;
        graph = vector<vector<int>>(roads.size() + 1);
        visited = vector<bool>(roads.size() + 1);
        for (auto& road : roads) {
            graph[road[0]].push_back(road[1]);
            graph[road[1]].push_back(road[0]);
        }
        dfs(0, seats);
        return ans;
    }
};

Python

# from typing import List

class Solution:
    def dfs(self, node: int) -> int:
        self.visited[node] = True
        cnt = 1
        for nextNode in self.graph[node]:
            if not self.visited[nextNode]:
                peopleFromThatNode = self.dfs(nextNode)
                cnt += peopleFromThatNode
                self.ans += (peopleFromThatNode + self.seats - 1) // self.seats
        return cnt
    
    def minimumFuelCost(self, roads: List[List[int]], seats: int) -> int:
        self.ans = 0
        self.graph = [[] for _ in range(len(roads) + 1)]
        for from_, to in roads:
            self.graph[from_].append(to)
            self.graph[to].append(from_)
        self.visited = [False] * (len(roads) + 1)
        self.seats = seats
        self.dfs(0)
        return self.ans