利用Sklearn框架实现简单线性回归,用于预测房价
前言:什么是sklearn框架和其他机器学习框架有何不同
Scikit-learn(简称sklearn)是一个基于Python编程语言的机器学习框架。它提供了丰富的机器学习算法和工具,可以帮助开发人员快速实现机器学习任务,例如分类、回归、聚类和降维等。同时,scikit-learn还提供了模型选择和评估、数据预处理和特征工程等功能,可以使机器学习的开发更加高效和方便。
与其他机器学习框架相比,scikit-learn的优点在于:
易于使用和上手。scikit-learn具有简单易懂的API,文档和示例丰富,可以帮助初学者快速掌握机器学习的基本概念和算法。
算法覆盖广泛。scikit-learn提供了大量的机器学习算法,包括监督学习、无监督学习和强化学习等多种类型,涵盖了各种不同的机器学习任务。
代码可移植性好。scikit-learn的代码可以在不同的平台和操作系统上运行,并且可以很容易地与其他Python库和框架集成。
社区支持强大。scikit-learn拥有庞大的用户社区和开发者社区,可以获得及时的技术支持和开发更新。
需要注意的是,与其他机器学习框架相比,scikit-learn也存在一些限制和缺点,例如对大规模数据集的处理能力较弱,缺乏深度学习算法的支持等。因此,在选择机器学习框架时,需要根据具体的任务和需求来进行综合评估和选择。
利用Sklearn框架实现简单线性回归,用于预测房价
# 导入Scikit-learn库和相关模块
from sklearn.linear_model import LinearRegression
import numpy as np
# 构造样本数据
x = np.array([1400, 1600, 1700, 1875, 1100, 1550, 2350, 2450, 1425, 1700])
y = np.array([245000, 312000, 279000, 308000, 199000, 219000, 405000, 324000, 319000, 255000])
# 将样本数据reshape为二维数组
x = x.reshape((-1, 1))
# 创建线性回归模型
model = LinearRegression()
# 将模型拟合到样本数据上
model.fit(x, y)
# 使用模型进行预测
x_test = np.array([2000]).reshape((-1, 1))
y_pred = model.predict(x_test)
# 输出预测结果
print("预测房价为:", y_pred)
![]()
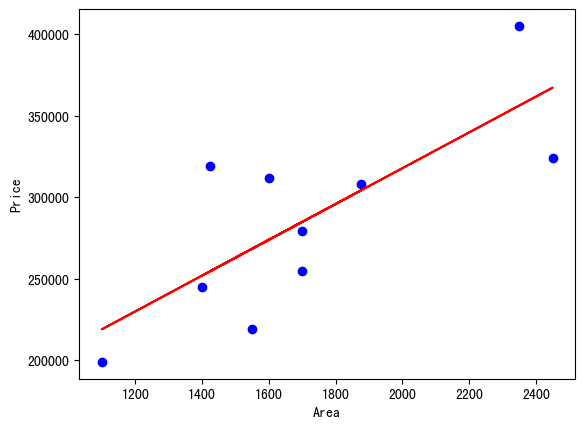
但是用这种方式,只是最终给了我们一个预测结果,我们想要更加直观的表现出来,即使用绘画的方式实现
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成样本数据
x = np.array([1400, 1600, 1700, 1875, 1100, 1550, 2350, 2450, 1425, 1700])
y = np.array([245000, 312000, 279000, 308000, 199000, 219000, 405000, 324000, 319000, 255000])
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(x.reshape(-1, 1), y)
# 预测结果
y_pred = model.predict(x.reshape(-1, 1))
# 绘制散点图和回归线图
plt.scatter(x, y, color='blue')
plt.plot(x, y_pred, color='red')
# 设置横轴和纵轴标签
plt.xlabel('Area')
plt.ylabel('Price')
# 显示图形
plt.show()
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# 生成样本数据
x = np.array([1400, 1600, 1700, 1875, 1100, 1550, 2350, 2450, 1425, 1700])
y = np.array([245000, 312000, 279000, 308000, 199000, 219000, 405000, 324000, 319000, 255000])
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(x.reshape(-1, 1), y)
# 预测结果
y_pred = model.predict(x.reshape(-1, 1))
# 绘制散点图和回归线图
plt.scatter(x, y, color='blue')
plt.plot(x, y_pred, color='red')
# 设置横轴和纵轴标签
plt.xlabel('Area')
plt.ylabel('Price')
# 显示图形
plt.show()