深入理解KMP算法
看这个算法之前,希望你做过:"leetcode-28-找出字符串中第一个匹配项的下标" 这一道题。
题目描述(直接上例子):
主串(T):leetcode
字串(P):leeto
在主串(T)中找出包含字串(P)的最小下标。
BF算法(暴力)
BF算法:下一个主串与子串不匹配时,满足以下条件 👇
1. 主串回退到此次开始匹配位置+1处;
2. 子串回退到0位置。
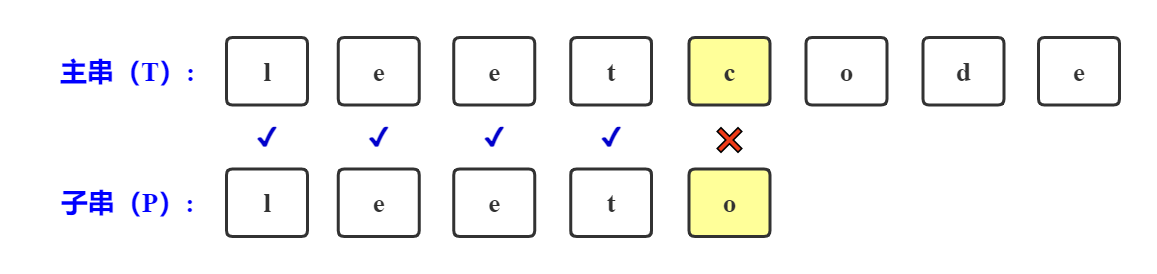
第一次比较
主串在'c'处与子串在'o'处不匹配
1. 主串回退到此次开始匹配位置+1,即是下标为1的位置;
2. 子串回退到0位置。
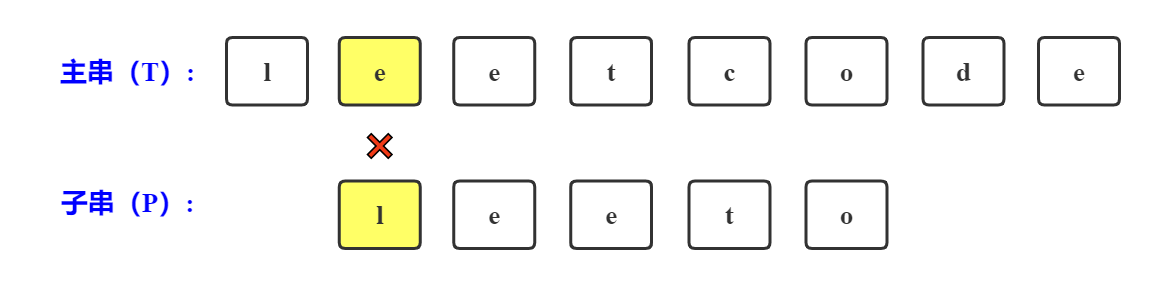
第二次比较
主串在'e'处与子串在'l'处不匹配
1. 主串回退到此次开始匹配位置+1,即是下标为2的位置;
2. 子串回退到0位置。
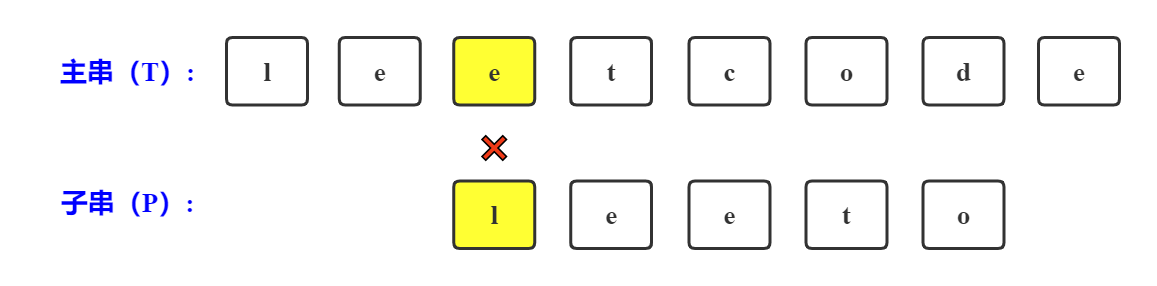
第三次比较
主串在'e'处与子串在'l'处不匹配
1. 主串回退到此次开始匹配位置+1,即是下标为3的位置;
2. 子串回退到0位置。
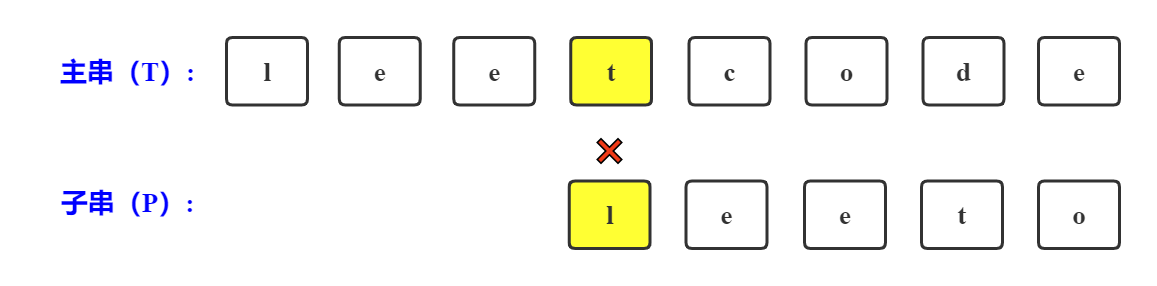
第四次比较
主串在't'处与子串在'l'处不匹配
1. 主串回退到此次开始匹配位置+1,即是下标为4的位置;
2. 子串回退到0位置。
下一次比较子串长度已经大于主串长度,不可能包含字串了,所以结束比较。
从上面的算法可以得出时间复杂度为:O((n-m)*m),其中n为主串字符串长度,m为子串字符串长度。
class Solution {
public int strStr(String haystack, String needle) {
int n = haystack.length(); // 主串(T)长度
int m = needle.length(); // 子串(P)长度
// 两个特例
if (n < m) return -1; // 子串(P)大于主串(T)
if (haystack.equals(needle)) { // 子串(P)等于主串(T)
return 0;
}
int end = n - m; // 控制提前结束,就是剩下的主串长度小于子串长度,不用比了,肯定不相等
for (int i = 0; i <= end; i++) {
if(haystack.charAt(i) != needle.charAt(0)) {
continue; // 子串开头就不等于主串的开头,跳过比较
}
int k = 0; // 子串与主串相等的字符个数
for (int j = i; j < i+m; j++, k++) {
if(haystack.charAt(j) != needle.charAt(k)){
break;
}
}
if(k == m){ // 一共有m个相等,即是找到答案啦,返回下标
return i;
}
}
return -1;
}
}KMP算法
KMP算法:下一个主串与子串不匹配时,满足以下两个条件 👇
1. 主串不回退;
2. 子串回退到特定位置。
理解2(子串回退到特定位置)之前,首先要了解一下"最长公共前后缀",这里是子串回退到哪的重点。
最长公共前后缀
首先,我先通过一个例子解释一下"最长公共前后缀",因为这个词可能表达得不是很正确,但是我找不到比这个更合适得词来描述这种情况了。
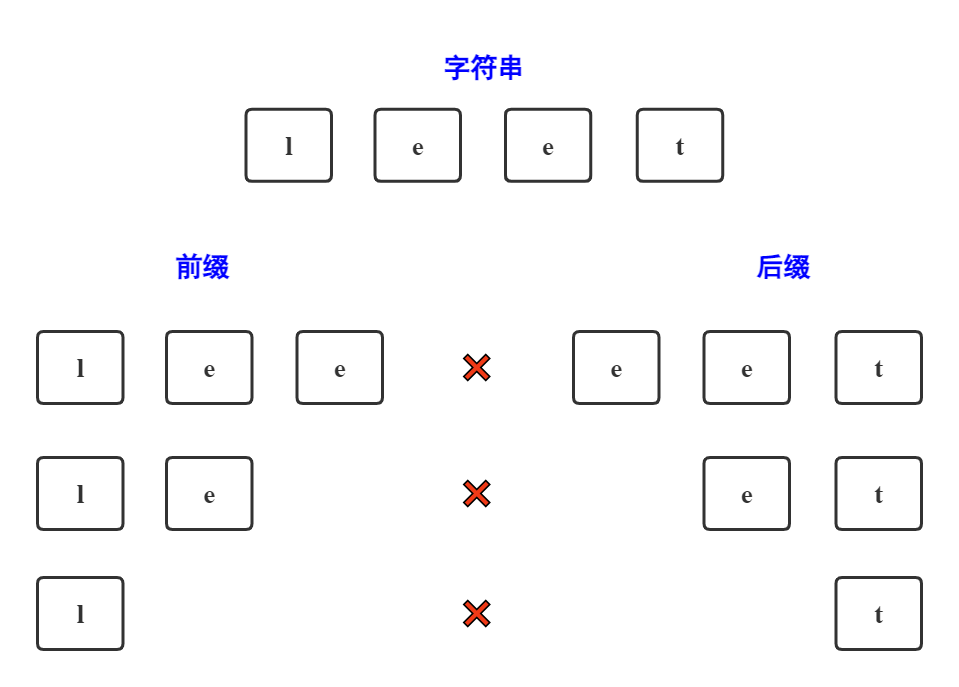
例如,上图中的例子,其中字符串为 "leet"。
前缀:包含第一个单词,不包含后一个单词的连续子串,则为前缀。
lee:包含第一个单词"l",不包含最后一个单词"t"
le:包含第一个单词"l",不包含最后一个单词"t"
l:包含第一个单词"l",不包含最后一个单词"t"
后缀:包含最后一个单词,不包含第一个单词的连续子串,则为后缀。
eet:包含最后一个单词"t",不包含第一个单词"l"
et:包含最后一个单词"t",不包含第一个单词"l"
t:包含最后一个单词"t",不包含第一个单词"l"
有了字符串的"前后缀"概念之后,我们可以找出子串的最长公共前后缀,例如上述例子中,字符串的最长公共前后缀为:0。因为没有一个前、后缀子串是相等的。
为了加深理解,再举一个例子:
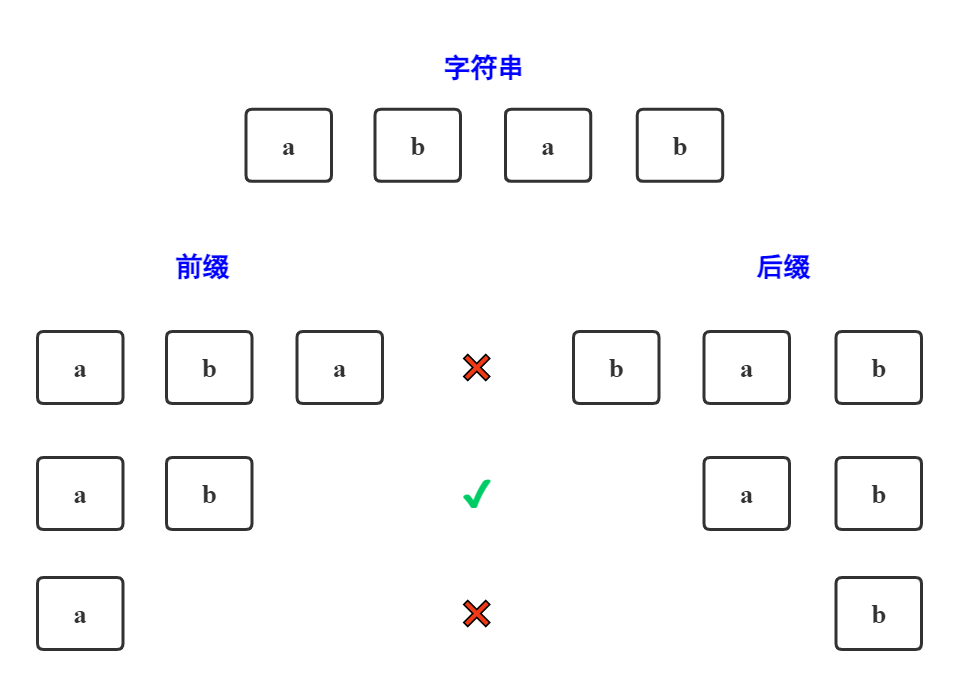
图中例子,字符串为:"abab",则最长的公共前后缀为2,因为,前缀"ab"=后缀"ab"。
回退数组
理解了最长公共前后缀,其实子串与主串匹配失败,应该回退到哪个位置,已经出现答案了。
举个例子:
主串:abeabababeabf
子串:abeabf
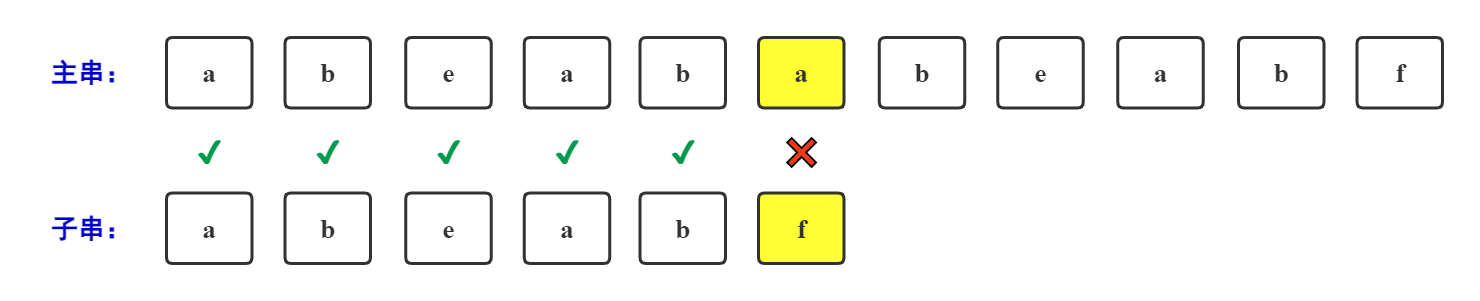
由图可得,主串在'a'处于子串在'f'处不相等,按照BF算法的回退过程,应该如下图所示:
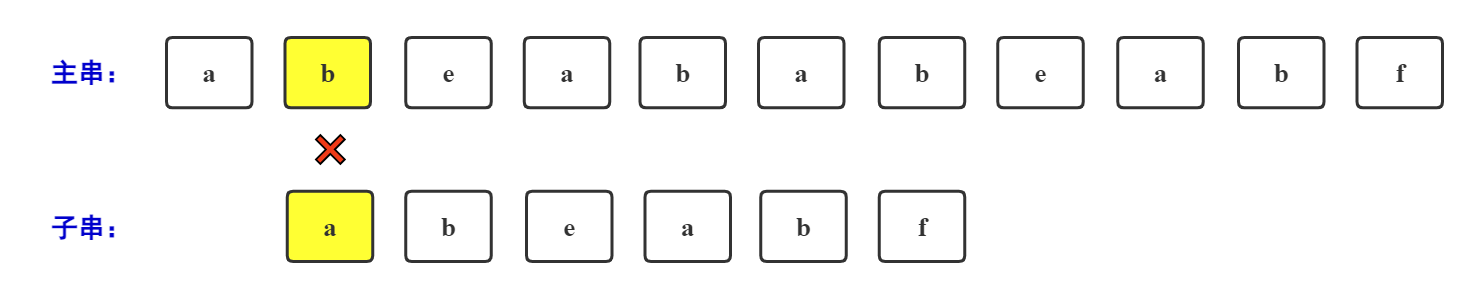
按KMP算法,回退如下图所示:
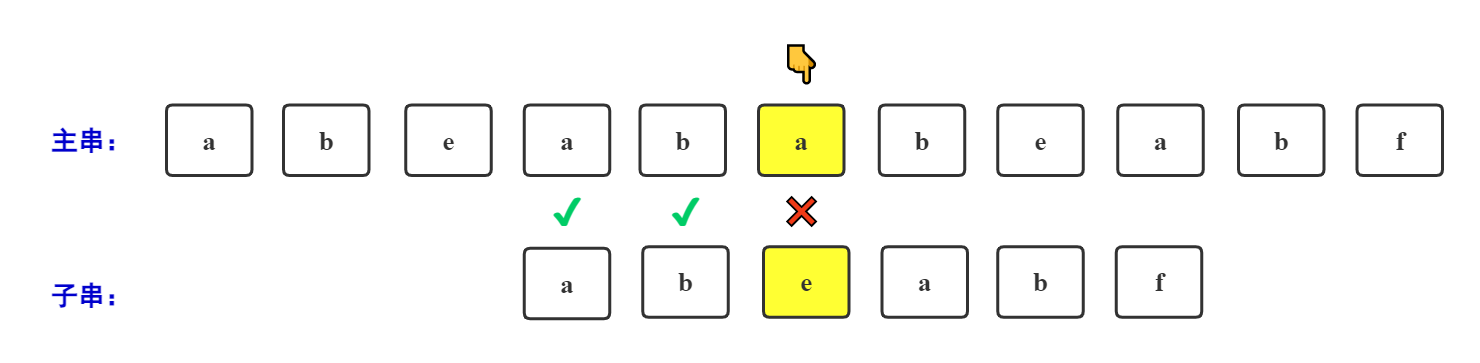
其实,这里就运用到"最长公共前后缀"的知识进行回退的。
主串在'a'处于子串在'f'处不相等,那么,前面字符串"abeab"其实已经之前比较过了(是相等的),那我们只需要找"abeab"的最长公共前后缀位置的下一个下标位置即可(这一步很关键,我尝试过多次入门KMP,但是都被这一步拒之门外,虽然这样做没错,但是为什么可以这么做??这其实也是我之前一直想知道为什么的一步,下面做一个解释)。
解释以下为什么只要找到最长公共前后缀位置的下标就是回退的位置!
匹配错误的字符串"abeaba",是在最后一个位置"a"处匹配错误的,是不是可以理解成有一对组合它以"a"为结尾与子串匹配不上。那我是不是可以找另一对组合,不是以"a"结尾的,但是前面是相同的。那我看一下前面有没有(看的这一步就是最长公共前后缀)。
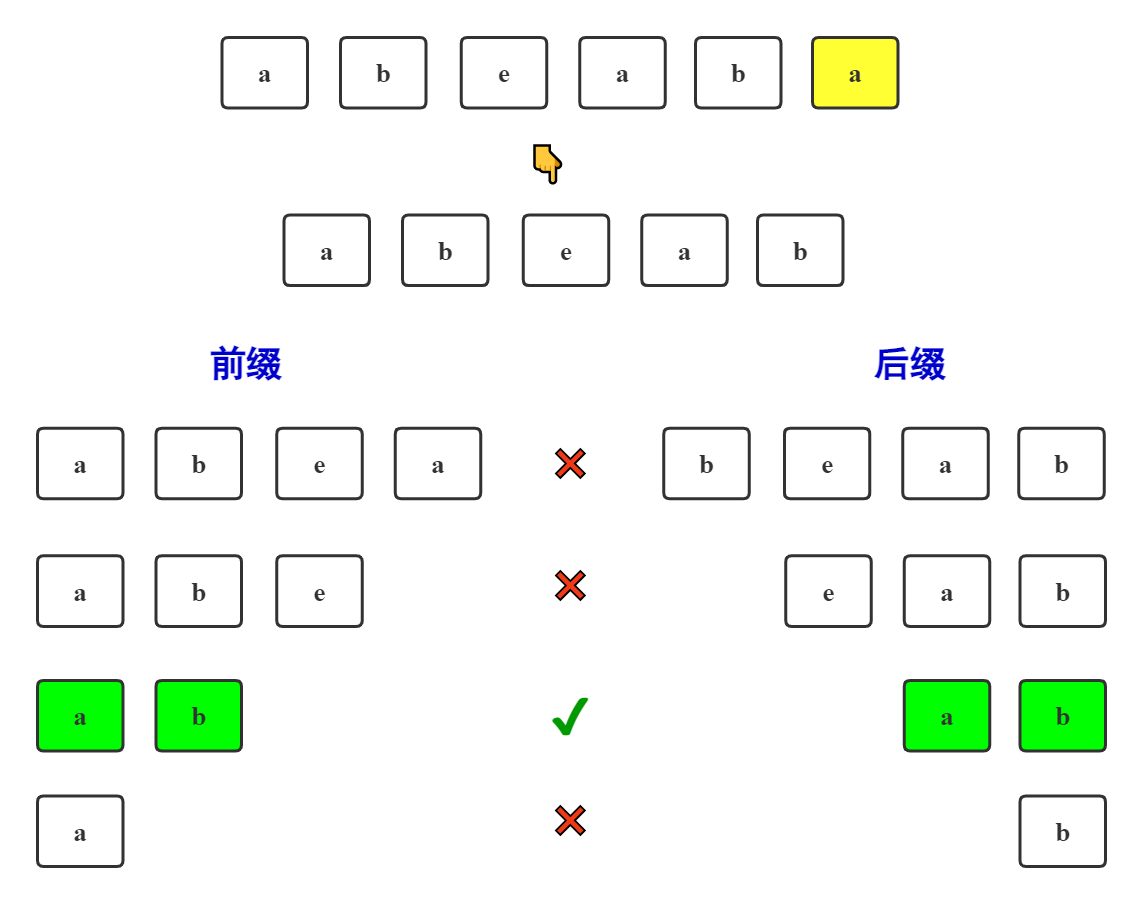
由图可得,找到了一对"ab",匹配错误的子串是"aba",但是这一对是"abe"。那我们就回退到最长公共前后缀位置的下一个下标位置即可。
class Solution {
public int strStr(String haystack, String needle) {
//int n = haystack.length(); // 主串(T)长度
//int m = needle.length(); // 子串(P)长度
//
两个特例
//if (n < m) return -1; // 子串(P)大于主串(T)
//if (haystack.equals(needle)) { // 子串(P)等于主串(T)
// return 0;
//}
//
//
//int end = n - m; // 控制提前结束,就是剩下的主串长度小于子串长度,不用比了,肯定不相等
//for (int i = 0; i <= end; i++) {
// if(haystack.charAt(i) != needle.charAt(0)) {
// continue; // 子串开头就不等于主串的开头,跳过比较
// }
// int k = 0; // 子串与主串相等的字符个数
// for (int j = i; j < i+m; j++, k++) {
// if(haystack.charAt(j) != needle.charAt(k)){
// break;
// }
// }
// if(k == m){ // 一共有m个相等,即是找到答案啦,返回下标
// return i;
// }
//}
//
//return -1;
int n = haystack.length(); // 主串(T)长度
int m = needle.length(); // 子串(P)长度
// 两个特例
if (n < m) return -1; // 子串(P)大于主串(T)
if (haystack.equals(needle)) { // 子串(P)等于主串(T)
return 0;
}
int[] next = getNext(needle); // 获取回退数组
for (int i = 0; i < m; i++) { // 打印回退数组
System.out.println(next[i]);
}
int i = 0; // 主串下标
int j = 0; // 子串下标
while (i < n){
if(haystack.charAt(i) == needle.charAt(j)) {
i++;
j++;
if(j == m) {
return i-m;
}
} else {
j = next[j]; // 不相等,则子串进行回退
if(j == -1){ // 到了第一个子串位置
j++;
i++;
}
}
}
return -1;
}
public int[] getNext(String str){
int n = str.length();
int[] next = new int[n];
next[0] = -1;
for (int i = 2; i < n; i++) {
String tempStr = str.substring(0, i);
int right = i-1;
int left = 1;
int find = 0;
while (left < i){
String leftStr = tempStr.substring(0, right);
String rightStr = tempStr.substring(left, i);
if (leftStr.equals(rightStr)){
find = leftStr.length();
break;
}
left++;
right--;
}
next[i] = find;
}
return next;
}
}