【面试经典150 | 二叉树】翻转二叉树

写在前面

本专栏专注于分析与讲解【面试经典150】算法，两到三天更新一篇文章，欢迎催更……

专栏内容以分析题目为主，并附带一些对于本题涉及到的数据结构等内容进行回顾与总结，文章结构大致如下，部分内容会有增删：

• Tag：介绍本题牵涉到的知识点、数据结构；
• 题目来源：贴上题目的链接，方便大家查找题目并完成练习；
• 题目解读：复述题目（确保自己真的理解题目意思），并强调一些题目重点信息；
• 解题思路：介绍一些解题思路，每种解题思路包括思路讲解、实现代码以及复杂度分析；
• 知识回忆：针对今天介绍的题目中的重点内容、数据结构进行回顾总结。

Tag

【递归】【迭代】【二叉树】

题目来源

226. 翻转二叉树

题目解读

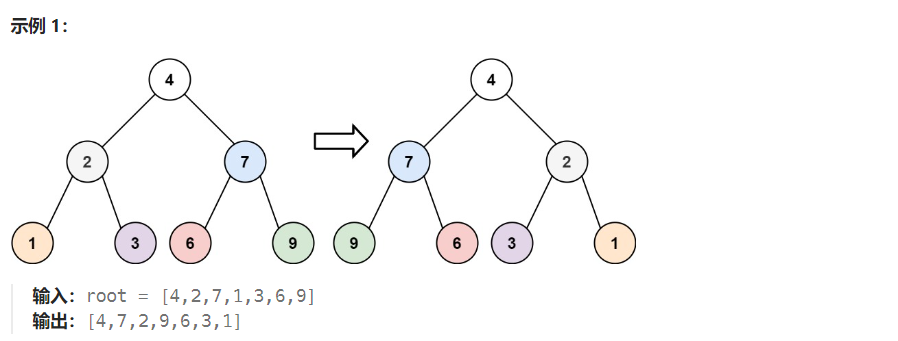
如示例 1 所示，翻转就是将二叉树的每个节点的所有子树都左右交换，原来父节点左子树现在变成了父节点的右子树，原来是父节点右子树现在变成了父节点的左子树。

解题思路

二叉树问题有两种解题方法，递归与迭代。

方法一：递归

思想

从根节点开始，先翻转左子树并记录翻转后的根节点 leftRoot，再翻转右子树并记录翻转后的根节点 rightRoot，然后将根节点的左子树替换为 rightRoot，右子树替换为 leftRoot。

算法

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == nullptr){
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);
        root->left = right;
        root->right = left;
        return root;
    }
};

复杂度分析

时间复杂度：$O(n)$，$n$ 为二叉树的节点个数。

空间复杂度：$O(n)$，最坏情况下二叉树退化成一条链，占用的栈空间为 $O(n)$。

方法二：迭代

思路

从根节点往下，按层枚举所有的节点，将每一个节点的左右子树进行交换就可以了。

算法

根节点为空，直接返回 nullptr。

根节点非空，则维护一个队列 q 用来记录节点。按照层序遍历的模板，依次交换左右子树：

• 首先，将根节点加入到队列 q；
• 接着，主要 q 不为空，就执行以下操作：
  • 弹出队首节点 node；
  • 只要该节点有子树（左右子树有一个节点或左右子树都存在），则交换两个子节点；
  • 将非空子节点加入到队列中。
• 最后返回翻转后的根节点 root。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }

        queue<TreeNode*> q;
        q.push(root);
        while (!q.empty()) {
            TreeNode* node = q.front();
            q.pop();
            if (node->left != nullptr || node->right != nullptr) {
                swap(node->left, node->right);
            }
            if (node->left) {
                q.push(node->left);
            }
            if (node->right) {
                q.push(node->right);
            }
        }
        return root;
    }
};

复杂度分析

时间复杂度：$O(n)$，$n$ 为二叉树的节点个数。

空间复杂度：$O(n)$。

写在最后

如果文章内容有任何错误或者您对文章有任何疑问，欢迎私信博主或者在评论区指出 💬💬💬。

如果大家有更优的时间、空间复杂度方法，欢迎评论区交流。

最后，感谢您的阅读，如果感到有所收获的话可以给博主点一个 👍 哦。