【SAS应用统计分析】方差分析
声明:本文知识参考内容来自网络,如有侵权请联系删除。
目录
【anova过程】
1.anova过程的语句格式
2.语句说明
【glm过程】
1.glm过程的语句格式
2.语句说明
【实例分析】
【实验步骤】
总结
【anova过程】
SAS系统的START软件提供了anova过程和glm过程等几个过程进行方差分析。
anova过程主要处理均衡数据,所谓均衡数据是指自变量的每种组合中的观察数是相等的,如果不相等则称为非均衡数据。对于均衡数据使用anova比使用glm计算快且占用内存少。如果实验设计不均衡,也不是上述的集中特定情况,那么应该使用glm过程。
1.anova过程的语句格式
anova过程的主要控制语句如下:
| proc anova | 指定分析的数据集名<选项列表>; |
| class | 变量列表; |
| model | 因变量列表=自变量列表 </选项列表>; |
| means | 效应列表 </选项列表>; |
| test | <H=效应列表> E = 效应列表; |
| run; |
其中class语句、model语句是必需的,而且class语句必需出现在model语句之前。test语句必需放在model语句之后。
2.语句说明
(1)proc means语句中的<列表选项>
- manova ---- 按多元方式删除哪些含有丢失值的观察,即在因变量中有丢失值就是从这次分析中删除这个观察
- outstat ---- 输出数据集名 生成一个输出数据集,它包含模型中每个效应的平方和、F统计量和概率水平
(2)class语句
在anova 过程中要使用的分类变量、区组变量必须首先在 clnss 语句的变量列表中说明class 语句是必需的,且必须放在 model 语前面。class 变量可以是数值型,也可以字符型。
(3)model语句
该语句用来规定因变量和自变量效应。如果没有规定自变量的效应,则只拟合截距,假设检验为因变量的均值是否为 0。model 语句的主要形式有四种 :
- 主效应模型
model y=a b c;
- 含有交叉因素的模型
model y-a b c a*b a*c b*c a*b*c;
- 嵌套模型
model y=a b c(a b);
- 包含嵌套、交叉和主效应的模型
modely=a b(a) c(a) b*c(a);
model 语句的选项列表有:int--打印与截距有关的假设检验结果。anova 过程总是把截距作为模型的一个效应进行处理,缺省时,不打印结果。
- nouni 不打印单变量分析结果
(4)means语句
该语句是用来计算在 means 语句后列出的每个效应所对应的因变量均值。anova 过程可以对出现在 model语句等号右边的任一效应计算因变量的均值。不过这些均值没有针对模型中的效应进行修正。如果需要修正的均值,应该调用glm 过程,使用其中的 Ismenas 语句。在anova过程里可以使用任意多个means 语句,它们放在model语句后面。
Means 语句的选项列表主要有两个内容,一是选择多重比较的检验方法,二是规定这些检验的细节,注意这些细节选项只能用于主效应。
多重比较的检验方法
- bon---对所有主效应均值之差进行 Bonferroni的t检验
- duncan---对所有主效应均值进行 Duncan 的多重极差检验。
- dunnett<('格式化对照值')>---进行 Dunnett 的双尾t检验。用以检验对所有主效应均值的某个水平作为对照,处理有无显著差异。为了规定这个对照效应的水平,在括号内用单引号把这个水平的格式化值括起来。缺省时,效应的第一个水平作为对照。
- dunnetl<('格式化对照值')>---进行 Dunnett 的单尾t检验。检验是否任一个处理显
著地小于这个对照。 - dunnettu<('格式化对照值')>---进行 Dunnett 的单尾t检验。检验是否任一个处理显著地大于这个对照。
- gabriel---对所有主效应均值进行 Gabriel的多重对比检验。
- regwf---对所有主效应均值进行 Ryan-Einot-Gabriel-Welsch 的多重F检验
- regwq---对所有主效应均值进行 Ryan-Einot-Gabriel-Welsch 的多重极差检验
- scheffe---对所有主效应均值进行 Scheffe 的多重对比检验
- sidak---对所有主效应局值水平依期 Sidak 不等式进行调整后,对其均值之差两两进行t检验
- Smm|gt2---当样本量不等时,基于学生化最大惯和 Sidak 不相关t不等式,使用Hochbeg 的 GT2方法,对主效应均值进行两两对比检验。
- snk-对所有主效应均值进行 Studen-Newmnn-Keuls 的多重极差检验。进行·检股。
- t|sd一对所有主效应均值进行两两 t 检验,它相当于在单元观察数相等时 Fishe的最小显著差 (Fisher's least-significant-dinerence)检验。
- tukey---对所有主效应均值进行 Tukey 的学生化极差检验。对所有主效应均值进行
- waller---对所有主效应均值进行 Waller-Duncan 的k 比率 (k-ratio) 检验。
多重比较的检验细节
- alpha=p--- 给出均值间对比检验的显著性水平。缺省值是 0.05。
- cldiff--- 要求把两两均值之差的结果用置信区间的形式输出。
- clm--- 对变量的每个水平的均值按置信区间形式输出。
- e=效应--- 指定在多重对比检验中所使用的误差均方.如果缺省,使用残差均方(MS)。指定的效应必须是在 model 语句中出现过的效应。
- kratio=值--- 给出 Waller-Ducan 检验的类型 1/类型2的误差限制比例。Kratio 的合理值为 50、100、500,大约相当于两水平时 alpha 值为 0.1、0.05、0.01 的情况。缺省值为100。
- lines--- 按下降次序列出所有检验方法产生的均值,并用一条线段在均值旁指出非显著的子集。
- hovtest---指定不同检验方法检验方差齐性,只适用于单因子方差分析,可供选择的方法有 hovtes=levenebartlett/bfjobrien。
(5)test语句
- 在分析中,如果这个语句缺省,仍然使用残差均方(MS)作为误差项对所有平方和((SS)计算F值。但用户可以使用本语句要求使用其他效应作为误差项,得到另外的F检验。可以使用多个 test 语句,把它们放在 model 语句后面。Test 语句的选项为:
- h=效应---规定模型里哪些效应用来作为假设的效应。
- e=效应---规定一个且只能是一个效应用来作为误差项,这个说明项是必需的
【glm过程】
1.glm过程的语句格式
Proc glm 是分析符合一般线性模型 (General Linear Models)的数据,因此取名 GLM。它能被用在许多不同的分析中,如简单回归、多元回归、方差分析、协方差分析、加权回归、多项式回归、偏相关分析、多元方差分析等。
在glm过程中的大多数方差分析的语句和选项与anova过程中基本相同。用anova过程编写的程序几乎不用修改就可在 glm 过程中运行。gm 过程仅仅附加了三条语句:contrast、estimate 和lsmeans。contrast和estimate 语句允许你测试和估计均值的某种功能。Ismeans语句允许你计算调整后的均值。
glm过程的主要控制语句如下:
| proc glm | 指定分析的数据集名<选项列表>; |
| class | 变量列表; |
| model | 因变量列表=自变量列表 </选项列表>; |
| contrast | '标签'效应 值表 </选项列表>; |
| estimate | '标签'效应 值表 </选项列表>; |
| lsmeans | 效应列表 </选项列表>; |
| means | 效应列表 </选项列表>; |
| output | <out = 输出数据集名><统计关键字=变量名列表>; |
| test | <H=效应列表> E = 效应列表; |
| run; |
其中,class语句、model语句是必须的,而且class语句必须出现在model语句之前,其他语句必须放在model语句之后,下面介绍anova过程相比不同的语句和新增加的语句。
2.语句说明
(1)model语句

(2)contrast语句



(3)Estimate语句

(4)Lsmeans语句

【实例分析】


【实验步骤】
步骤一,单因素方差分析(例3.1)
data veneer;
input brand $ wear @@;
cards;
ACME 2.3 ACME 2.1 ACME 2.4 ACME 2.5
CHAMP 2.2 CHAMP 2.3 CHAMP 2.4 CHAMP 2.6
AJAX 2.2 AJAX 2.0 AJAX 1.9 AJAX 2.1
TUFFY 2.4 TUFFY 2.7 TUFFY 2.6 TUFFY 2.7
XTRX 2.3 XTRX 2.5 XTRX 2.3 XTRX 2.4
;
ods html file = 'D:\SAS\sasdata\shiyan\new.html';
proc anova data = veneer;/*调用anova过程进行单因素方差分析*/
class brand; /*class必须放在model与means之前,用于指明统计模型的自变量*/
model wear = brand; /*model语句是因变量=实验效果值,因变量为wear*/
means brand /hovtest;/*选项hovtest计算不同品牌经济方财胄灶的假设检验*/
run;
ods html close;
程序的运行结果如下:
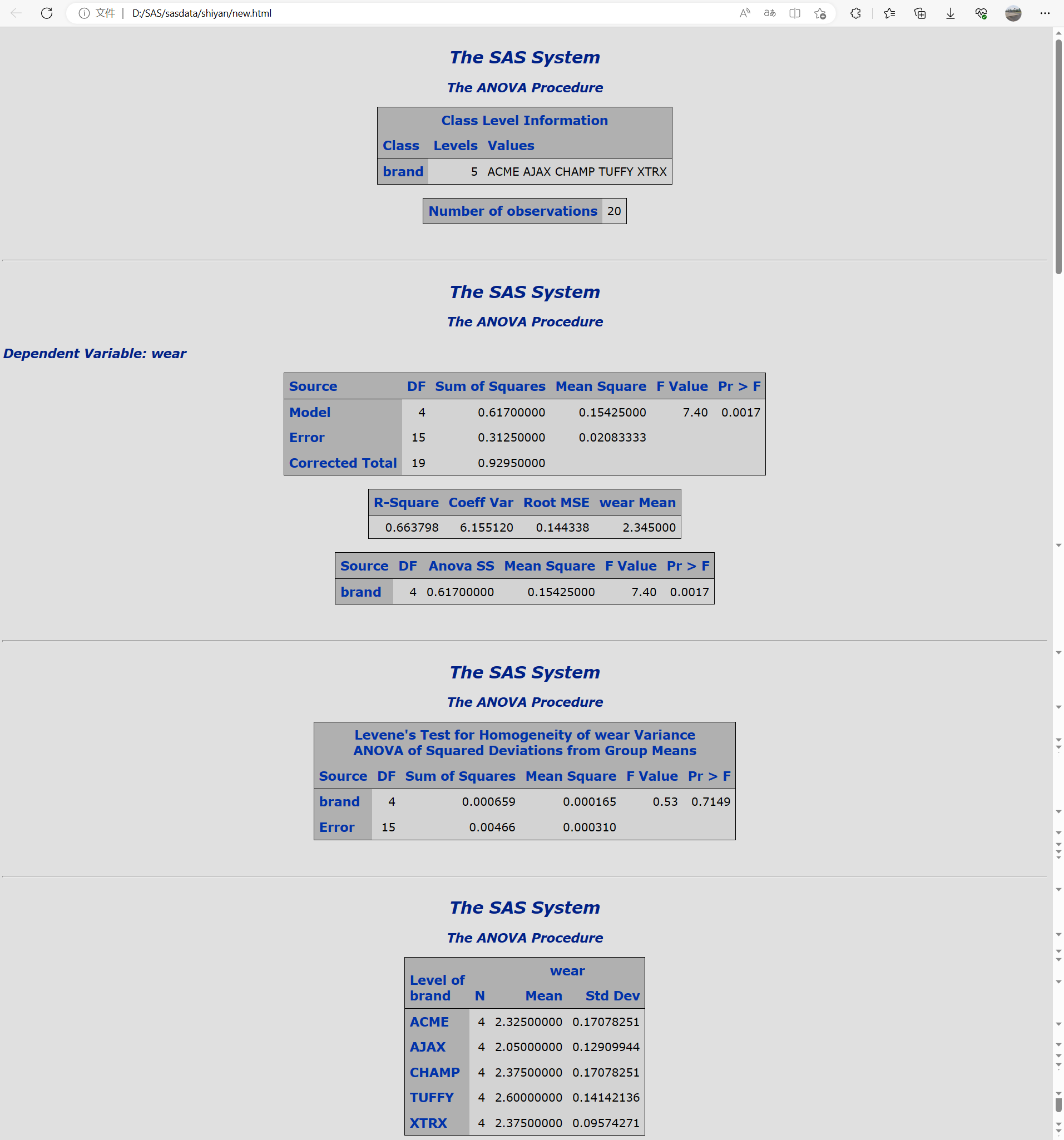
结果由五部分组成:
(1)给出类水平信息:分类变量为brand,该水平量有5个水平,变量取ACME,AJAX,CHAMP,TUFFY,XTRE,以及数据集中有20个观测值(此处忽略)
(2)方差部分分析:

对模型的F检验与对分组变量的F检验结果时一致的,因为Model语句中唯一的变差来源就是这一个变量。
(3)Levene的方差齐性检验部分:检验结果表明,不能拒绝不同品牌组间观测值的方差是相等的 假设。
(4)输出了每种品牌的观测值、均值和标准差。
方差分析的结果表明,总体F检验是极显著的,说明模型是有意义的。品牌的F检验也是极显著的,说明至少有两种品种的树高生长量(平均值)有显著差异,但并没有指明具体哪些品种之间有差异,需要通过多重比较来实现。程序如下:
data veneer;
input brand $ wear @@;
cards;
ACME 2.3 ACME 2.1 ACME 2.4 ACME 2.5
CHAMP 2.2 CHAMP 2.3 CHAMP 2.4 CHAMP 2.6
AJAX 2.2 AJAX 2.0 AJAX 1.9 AJAX 2.1
TUFFY 2.4 TUFFY 2.7 TUFFY 2.6 TUFFY 2.7
XTRX 2.3 XTRX 2.5 XTRX 2.3 XTRX 2.4
;
proc anova data = veneer;
class brand;
model wear = brand;
means brand/duncan;/*使用means语句进行多重比较,选项duncan是要求计算输出组间均值比较多的多重极差检验*/
means brand/lsd clm cldiff; /*使用means语句进行多重比较,选项lsd clm cldiff分别要求对各组间均值之间采用最小显著差检验,输出组间的均值及均值置信区间、各组均值之差的置信区间*/
run;
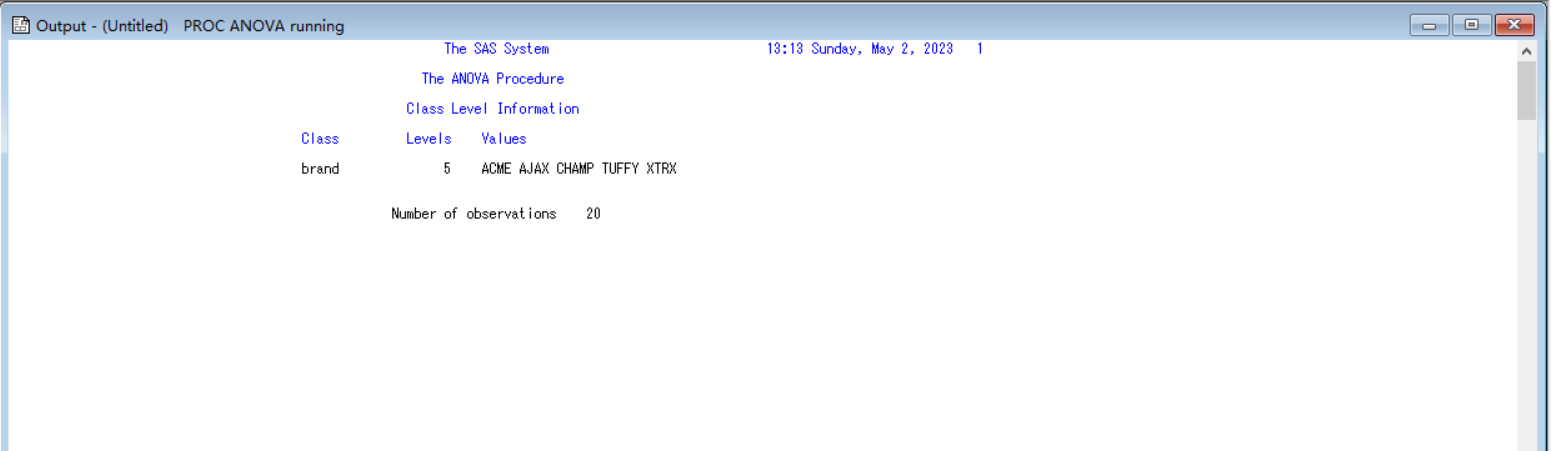
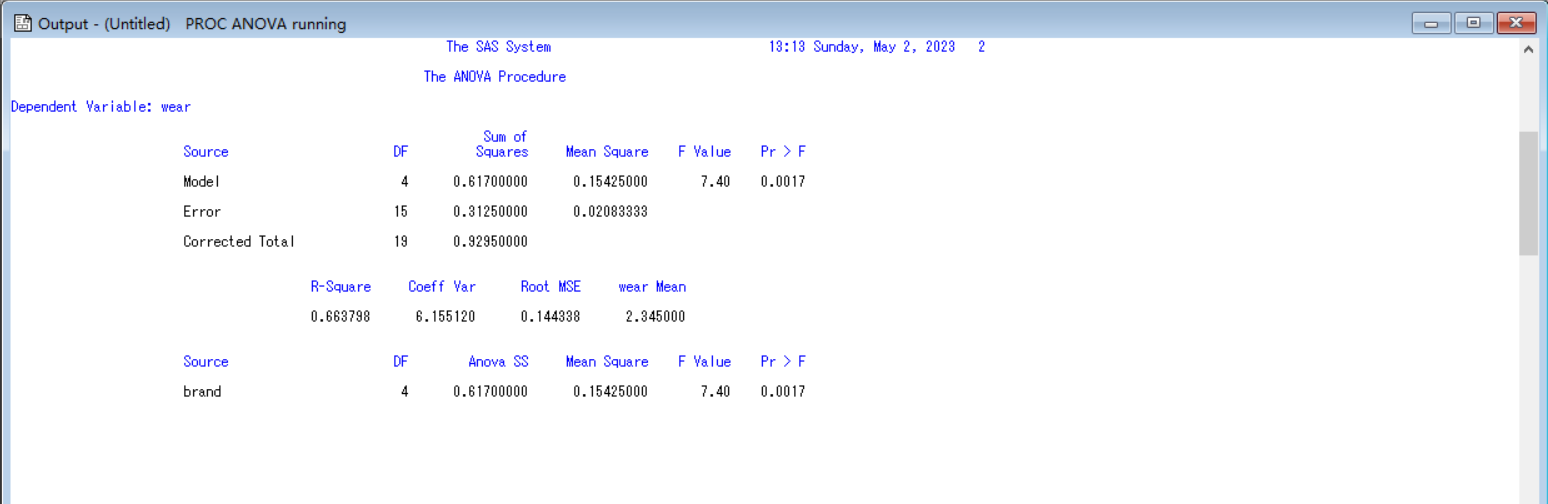
(1)程序运行的主要结果
(2)均值的两两t检验、各组均值的置信区间及采用最小显著差检验


步骤二,双因素方差分析(考虑交互作用)(例3.2)
options linesize=76;
data shoushizhe;
do a=60 to 120 by 20;
do b=1 to 4;
do i = 1 to 2;
input energy @@ block; output;
end;
end;
end;
drop i;
cards;
2.70 3.30 1.71 2.14 1.90 2.00 2.72 2.85
1.38 1.35 1.74 1.56 3.14 2.29 3.51 3.15
2.35 1.95 1.67 1.50 1.63 1.05 1.39 1.72
2.26 2.13 3.14 2.56 3.17 3.18 2.22 2.19
;
run;
proc anova data =shoushizhe;
class a b;
model energy = a b a*b;
test h = a e=a*b;
means a/duncan e= a*b;
run;
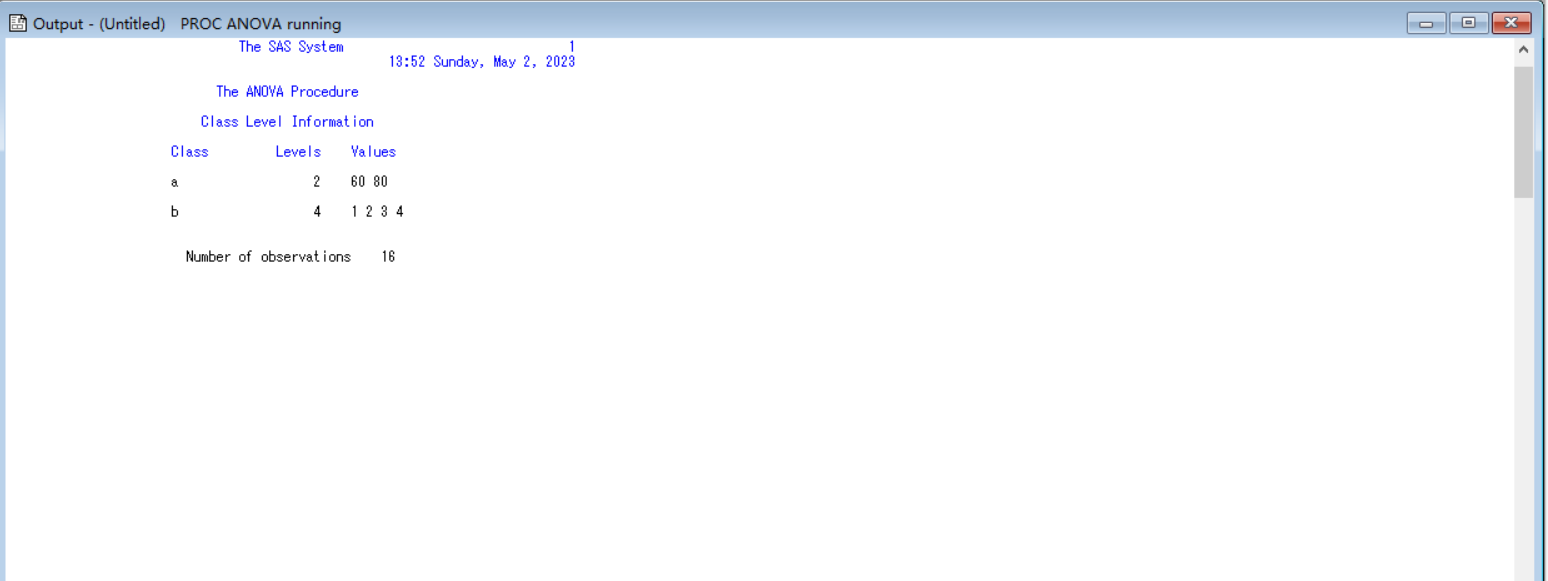
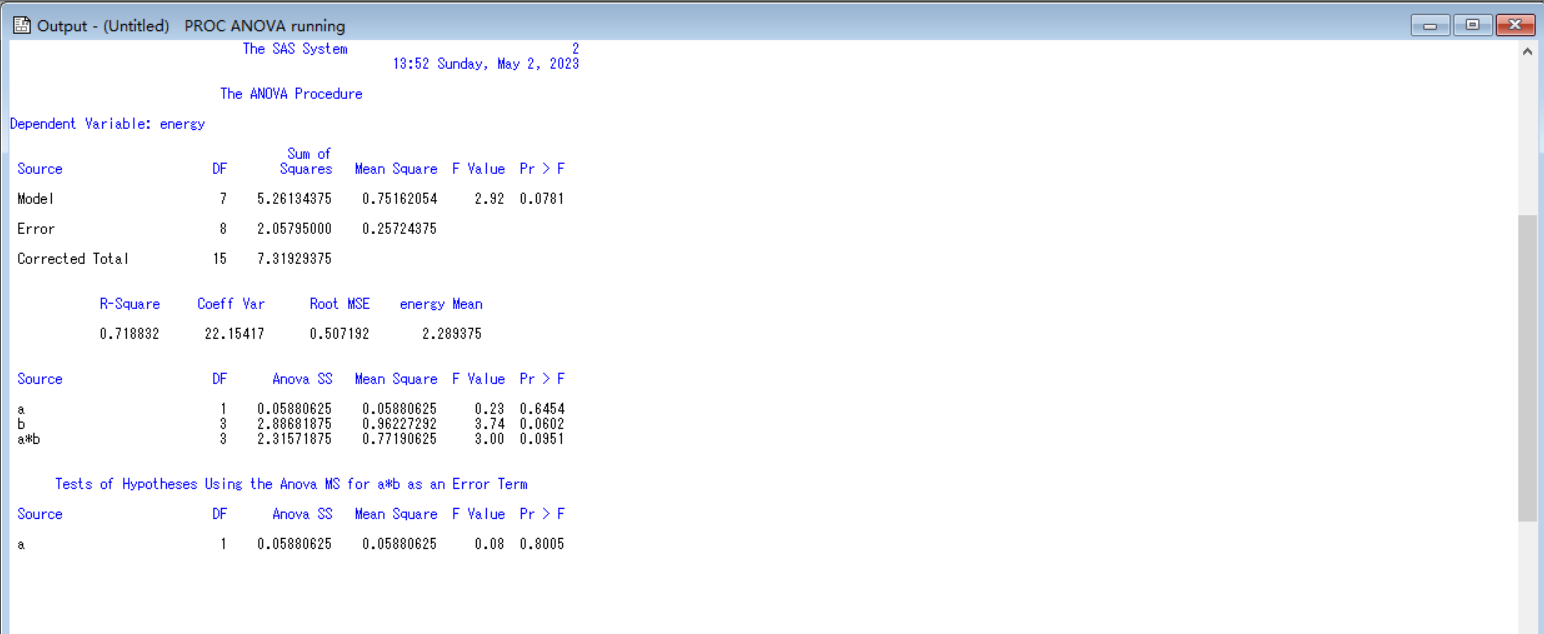

步骤四,不等重复实验的方差分析
data turang;
do soil=1 to 3;
input m @@;
do repl =1 to m;
input height @@;output;
end;
end;
drop repl;
cards;
5 53 47 41 43 48
8 64 62 57 70 71 82 78
6 56 61 52 48 52 46
;
proc glm;
class soil;
model height=soil;
quit ;
run;

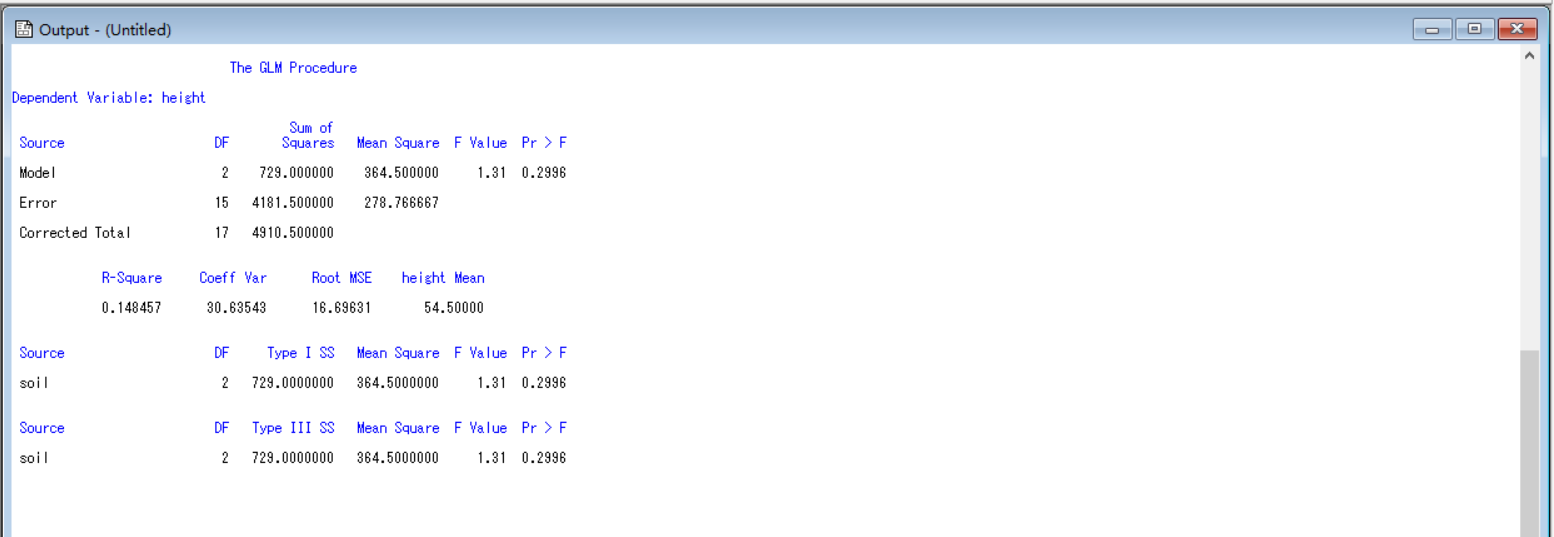
总结
- 掌握用anova过程分别进行单因素方差分析和等重复的双因素方差分析
- 掌握用glm过程进行不等重复的方差分析
- 了解do语句的格式和用法
