2023第十二届“认证杯”数学中国数学建模国际赛赛题A完整解析
A题完整题解
- 写在前面
- 假设
- 数据预处理
- 问题一
- 1 基于自适应ARIMA-BP神经网络模型的影响因素预测
- 1.1 ARIMA模型的建立
- 1.2 BP神经网络模型的建立
- 1.3 基于GABP神经网络的预测模型构建
- 1.4 自适应混合ARIMA-BP神经网络模型的建立
- 1.5 模型求解
- 代码
- Q1_1.m
- Q1_2.m
- 完整代码与论文获取
写在前面
发布赛题一直到现在,总算完成了认证杯A题完整的解题过程,包括代码完整代码与结果、解题思路、模型文档与论文框架~
学姐的代码和论文框架保证原创,保证高质量哦,都是跟国奖学长一起努力完成的!!
假设
数据预处理
磁场数据中包含缺失值,故需对缺失值进行插补。在本文中,利用拟合模型对缺失值的进行插补。基于拟合的插补方法的一般步骤如下:
1、收集已有数据:首先,需要收集包含缺失数据的数据集。确保数据集中有足够的样本和特征来进行非线性拟合。
2、建立模型:选择适当的模型来拟合已有数据。常见的非线性模型包括多项式回归、指数函数、对数函数、幂函数等。根据数据的特点和领域知识,选择合适的模型。
3、拟合已有数据:使用已有数据来拟合选定的非线性模型。可以使用回归分析等方法来估计模型的参数。
4、预测缺失数据:使用拟合好的非线性模型来预测缺失数据的值。将已有数据中的特征值代入模型,得到对应的预测值。
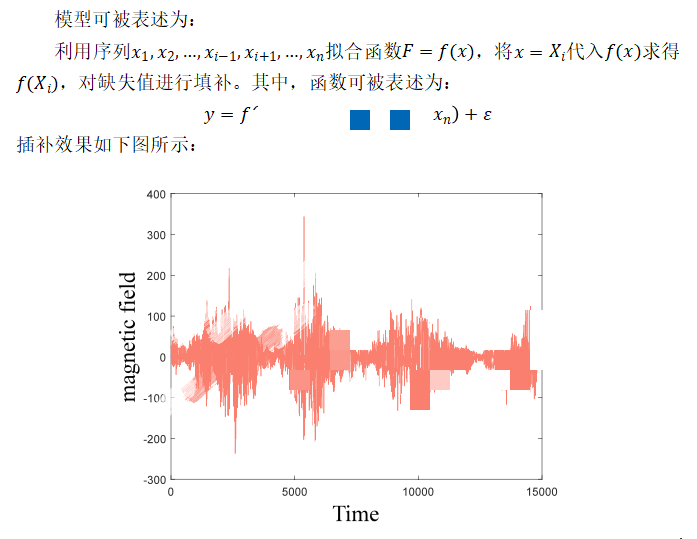
其次,题目中要求以月份为单位对数值进行统计,而原始数据集的统计单位时日。故对日期进行转换,得到以月为单位的序列图如下所示:
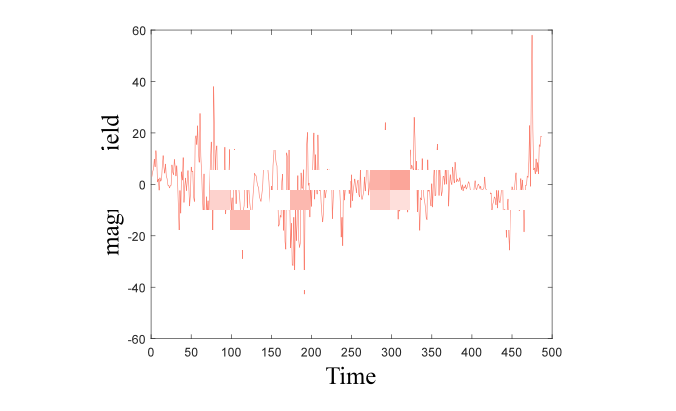
问题一
1 基于自适应ARIMA-BP神经网络模型的影响因素预测
在本章中,基于自适应ARIMA-BP神经网络模型对数据进行预测。
1.1 ARIMA模型的建立

1.2 BP神经网络模型的建立
BP神经网络是是一种多层前馈算法,由输入层、隐含层和输出层组成。层与层之间有工作信号与误差信号传播。如下图所示为神经网络结构图。
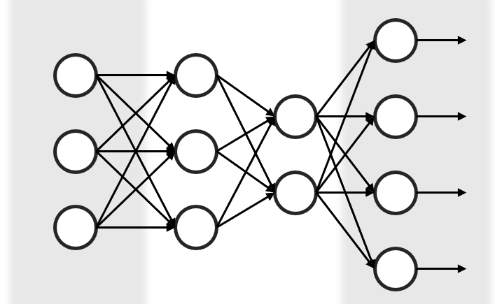
BP神经网络的运算原理如下:
在这里插入图片描述
1.3 基于GABP神经网络的预测模型构建
(这里写一段话,描述一下问题的复杂度,引出为什么要在BP的基础上设计GABP
本文采用遗传算法对BP神经网络的进行了优化,并在迭代过程中利用BP神经网络的前向传播过程来计算每个个体的适应度,以此来提升算法的优化效率。算法的设计框架如算法如下所示。

在遗传算法的编码环节,IGABP将神经网络的权重和阈值连续地表示为一个向量,用于构成个体基因的表达。由于在算法运行过程中网络的结构已经确定,所需确定的权重及阈值数量也已经被确定,故在迭代过程中染色体的长度保持不变。
在遗传算法中计算个体适应度的部分,相比GABP使用解码后的个体初始化神经网络,然后根据训练后的输出计算适应度,IGABP从原理上着手,利用神经网络前向传播的过程,直接计算个体的适应度,免去了训练所需的计算量,提高了算法的优化效率。
编码及解码
假设BAGP中所使用的神经网络如下图所示:
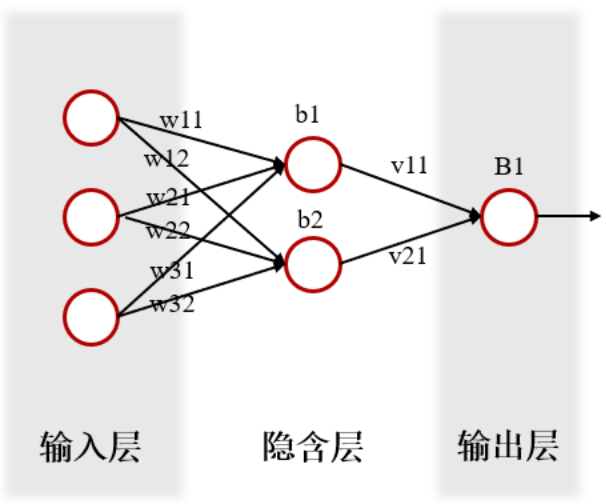
则在确定网络的权重和阈值时,可以设计编码结构为:

在本文所设计的染色体中,基因位依次分别表述:输入层与隐含层之间的权值、隐含层的阈值、隐含层与输出层之间的权值,输出层的权值。由此,即可确定一个神经网络完整的结构。
在本文所设计的染色体中,基因位依次分别表述:输入层与隐含层之间的权值、隐含层的阈值、隐含层与输出层之间的权值,输出层的权值。由此,即可确定一个神经网络完整的结构。
1.4 自适应混合ARIMA-BP神经网络模型的建立
对于每一预测算法,均通过部分序列作为测试集。本文所设计的混合算法的混合思想主要为:在往期的预测中性能越好则在未来的预测中的权重就越高,对预测值的贡献度就越高。

式中,为算法k在混合算法中的权重。在每次计算混合预测值时,需要将ARIMA算法与BP神经网络算法的预测值结合起来。其计算公式可以表述为:
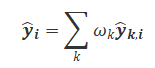
1.5 模型求解
模型求解结果如下:
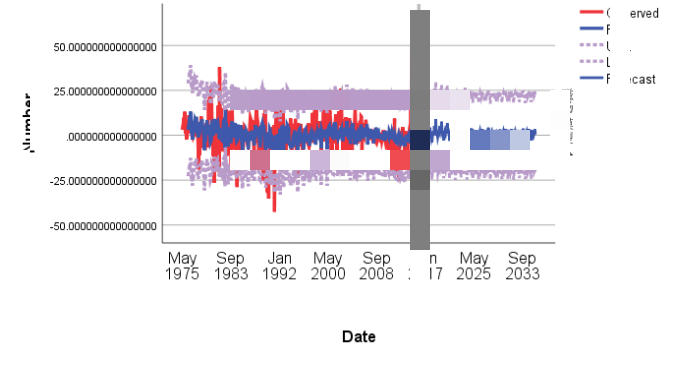
(分析一下预测结果,识别出了波动。。。。)

结合黑子数进行分析,解得下一个太阳周期的开始时间约为2031年,结束时间约为2042年。
代码
Q1_1.m
clc
clear
data=xlsread('磁场.xlsx');
for i=1:size(data,1)
if isnan(data(i,3))
if isnan(data(i-1,3))
data(i,3)=data(i+1,3);
elseif isnan(data(i+1,3))
data(i,3)=data(i-1,3);
else
data(i,3)=round((data(i-1,3)+data(i+1,3))/2);
end
end
end
color=[250/255,127/255,111/255;
130/255,176/255,210/255;
190/255,184/255,220/255;
231/255,218/255,210/255;
153/255,153/255,153/255];
plot([1:1:size(data,1)],data(:,3),'color',color(1,:))
set(gcf,'Color',[1 1 1])
xlabel({'Time'},'Color','k','FontSize',20,'FontName','Times New Roman')
ylabel({'magnetic field'},'Color','k','FontSize',20,'FontName','Times New Roman')
Q1_2.m
clc
clear
data=xlsread('磁场.xlsx');
index=[];
M=Inf;
for i=1:size(data,1)
if data(i,2)~=M
index=[index;i];
M=data(i,2);
end
end
index=[index;size(data,1)+1];
new_data=[];
for i=1:size(index,1)-1
temp_data=data(index(i):index(i+1)-1,:);
new_data(i,1:2)=temp_data(1,1:2);
new_data(i,3)=mean(temp_data(:,3));
end
color=[250/255,127/255,111/255;
130/255,176/255,210/255;
190/255,184/255,220/255;
231/255,218/255,210/255;
153/255,153/255,153/255];
plot([1:1:size(new_data,1)],new_data(:,3),'color',color(1,:))
set(gcf,'Color',[1 1 1])
xlabel({'Time'},'Color','k','FontSize',20,'FontName','Times New Roman')
ylabel({'magnetic field'},'Color','k','FontSize',20,'FontName','Times New Roman')
完整代码与论文获取
目前只分享第一问哦,以下是我们的论文框架、技术模板,代码以及使用到的数据。有需要的小伙伴看下面哦