【C语言】操作符详解(一):进制转换,原码,反码,补码
目录
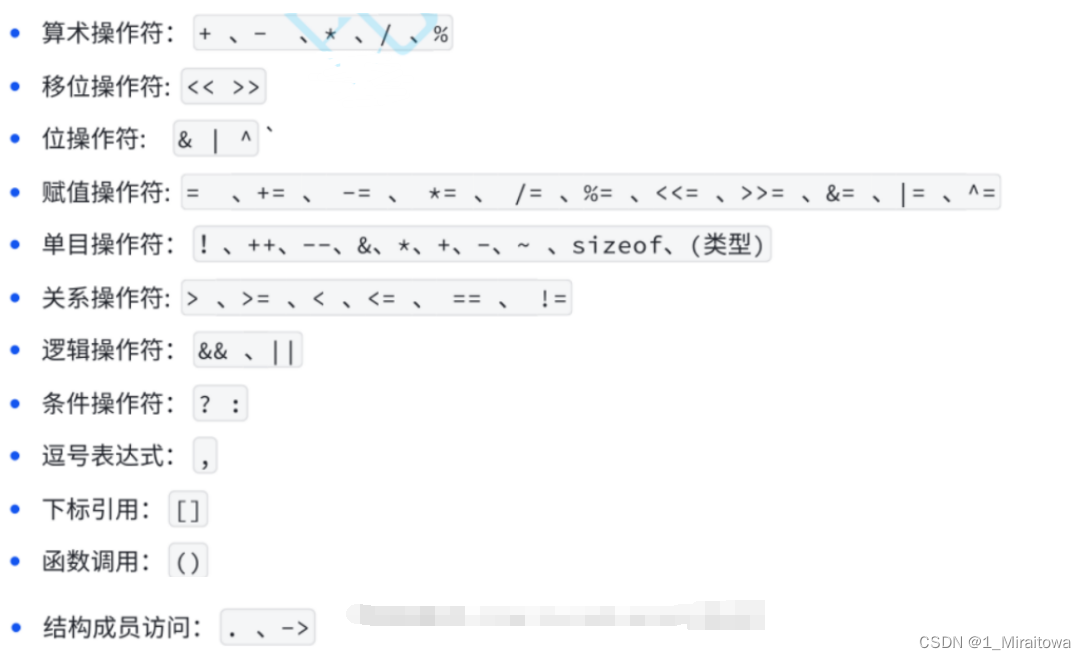
操作符分类
2进制和进制转换
2进制转10进制
10进制转2进制
2进制转8进制和16进制
2进制转8进制
2进制转16进制
原码、反码、补码
操作符分类
操作符中有一些操作符和二进制有关系,我们先铺垫一下二进制的和进制转换的知识。
2进制和进制转换
其实我们经常能听到2进制、8进制、10进制、16进制这样的讲法,那是什么意思呢?其实2进制、8进制、10进制、16进制是数值的不同表示形式而已。
比如:数值15的各种进制的表示形式:
15的2进制:1111
15的8进制:17
15的10进制:15
15的16进制:F
我们重点介绍一下二进制:
首先我们还是得从10进制讲起,其实10进制是我们生活中经常使用的:
⭐10进制中满10进1。
⭐10进制的数字每一位都是0~9的数字组成。
其实2进制也是一样:
⭐2进制中满2进1。
⭐2进制的数字每一位都是0~1的数字组成那么1101就是二进制的数字了。
2进制转10进制
其实10进制的123表示的值是一百二十三,为什么是这个值呢?其实10进制的每一位是权重的,10进制的数字从右向左是个位、十位、百位.....,分别每一位的权重是
如下图:
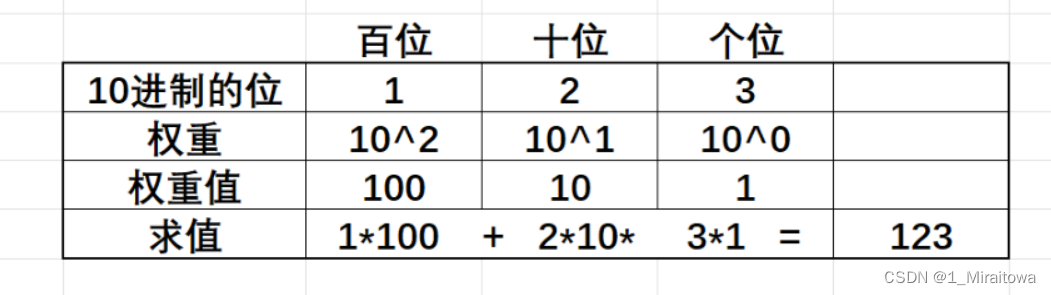
2进制和10进制是类似的,只不过2进制的每一位的权重,从右向左是:如果是2进制的1101,该怎么理解呢?

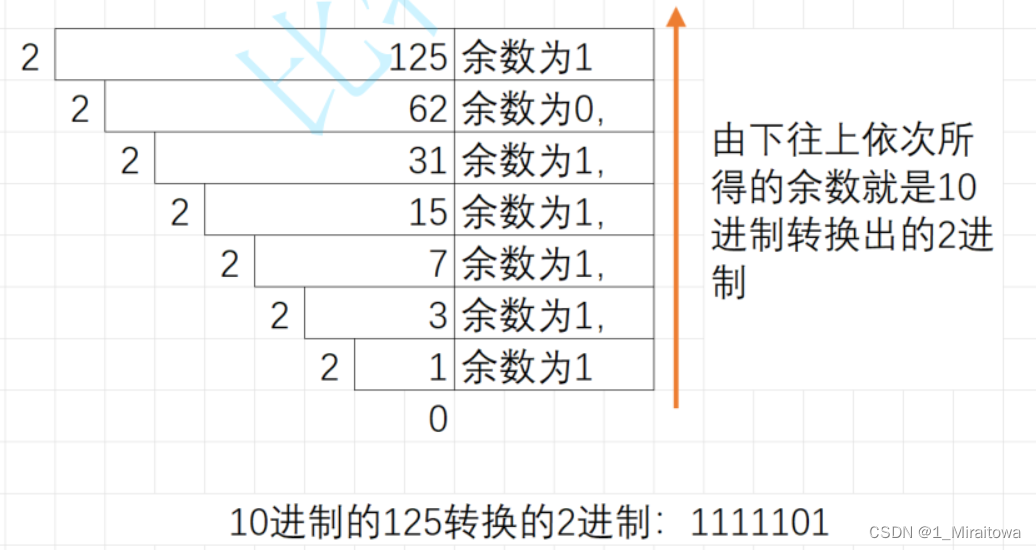
10进制转2进制
2进制转8进制和16进制
2进制转8进制
8进制的数字每一位是0~7的,0~7的数字,各自写成2进制,最多有3个2进制位就足够了,比如7的二进制是111,所以在2进制转8进制数的时候,从2进制序列中右边低位开始向左每3个2进制位会换算一个8进制位,剩余不够3个2进制位的直接换算。
如:2进制的01101011,换成8进制:0153,0开头的数字,会被当做8进制。

2进制转16进制
16进制的数字每一位是0~9,a ~f的,0~9,a ~f的数字,各自写成2进制,最多有4个2进制位就足够了,比如f的二进制是1111,所以在2进制转16进制数的时候,从2进制序列中右边低位开始向左每4个2进制位会换算一个16进制位,剩余不够4个二进制位的直接换算。
如:2进制的01101011,换成16进制:0x6b,16进制表示的时候前面加0x
原码、反码、补码
整数的2进制表示方法有三种,即原码、反码和补码
有符号整数的三种表示方法均有符号位和数值位两部分,2进制序列中,最高位的1位是被当做符号位,剩余的都是数值位。 符号位都是用0表示“正”,用1表示“负”。
🔺正整数的原、反、补码都相同
🔺负整数的三种表示方法各不相同
原码:直接将数值按照正负数的形式翻译成二进制得到的就是原码。
反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。
补码:反码+1就得到补码。
反码得到原码也是可以使用:取反,+1的操作。
对于整形来说:数据存放内存中其实是存放的补码
为什么呢?
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理; 同时,加法和减法也可以统一处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
以上便是我为大家带来的进制转换,原码,反码,补码内容,若有不足,望各位大佬在评论区指出,谢谢大家!可以留下你们点赞、收藏和关注,这是对我极大的鼓励,我也会更加努力创作更优质的作品。再次感谢大家!

