嗯,这个树怎么和往常不一样?
文章目录
- 前言
- 一、二叉树的链式存储
- 二、二叉树链式结构的实现
- 二叉树的结构设计
- 手动构建二叉树
- 二叉树的前序遍历
- 二叉树的中序遍历
- 二叉树的后序遍历
- 二叉树的层序遍历
- 计算二叉树大小
- 计算叶子节点个数
- 计算二叉树高度
- 计算第K层的节点个数
- 查找某个值对应的节点
- 二叉树的销毁
- 三、完整代码
- test.c
前言
今天五一假期,学习了数据结构的二叉树相关内容,所以写这一篇博客来记录自己的学习内容,主要就是重点知识的梳理。
一、二叉树的链式存储
概念:二叉树的链式存储结构是指用
链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。
结构示意图:
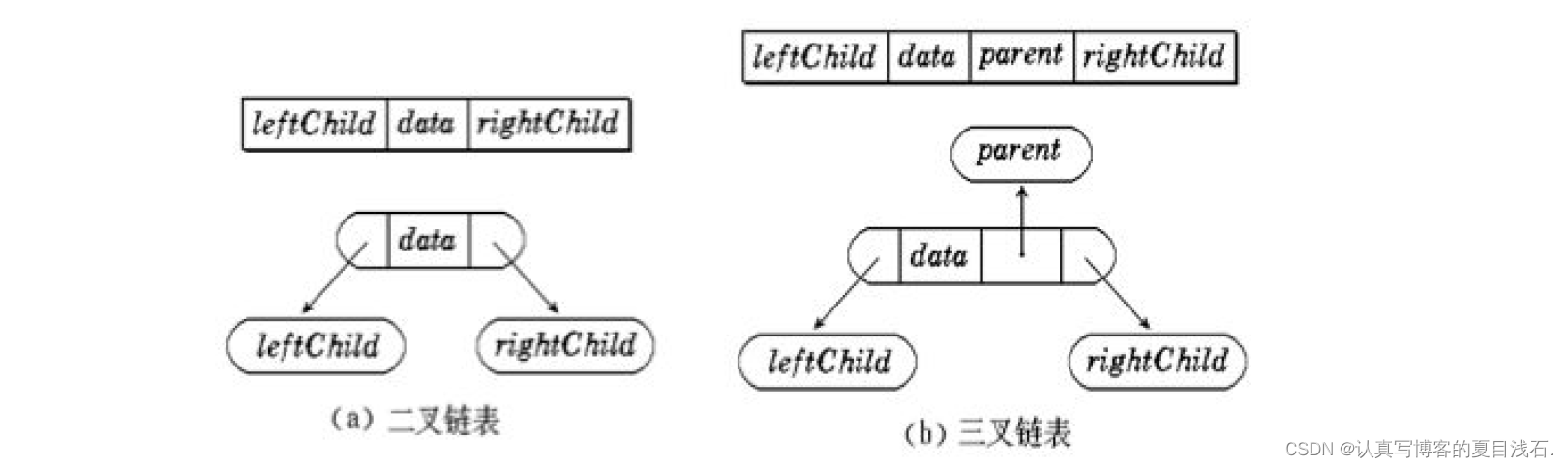
逻辑结构:
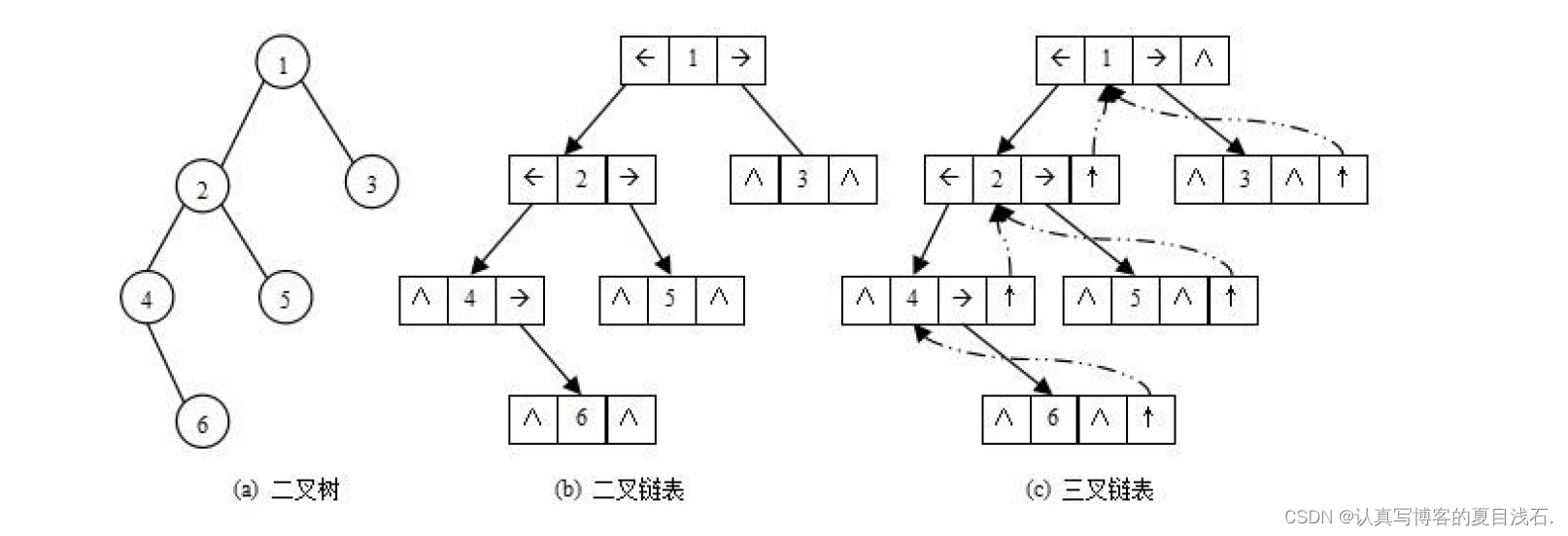
二叉链和三叉链的结构设计:
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{
struct BinTreeNode* left; // 指向当前节点左孩子
struct BinTreeNode* right; // 指向当前节点右孩子
BTDataType data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{
struct BinTreeNode* parent; // 指向当前节点的双亲
struct BinTreeNode* left; // 指向当前节点左孩子
struct BinTreeNode* right; // 指向当前节点右孩子
BTDataType data; // 当前节点值域
};
二、二叉树链式结构的实现
在学习二叉树的基本操作前,需要创建一棵二叉树,然后才能学习其相关的基本操作。为了降低学习成本,我们直接手动创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
而对于增删查改等功能,对于我们当前学习的二叉树并没有价值,所以我们的学习主要围绕遍历二叉树,或者计算节点或高度来进行。
二叉树的结构设计
此处我们使用的结构为 二叉链 的结构
typedef int BTDataType;
//二叉链
struct BinaryTreeNode
{
struct BinaryTreeNode* left; //指向当前节点的左孩子
struct BinaryTreeNode* right; //指向当前节点的右孩子
BTDataType data; //当前节点的值
}
手动构建二叉树
本篇博客 我构建了一颗简单的二叉树,如下图所示:
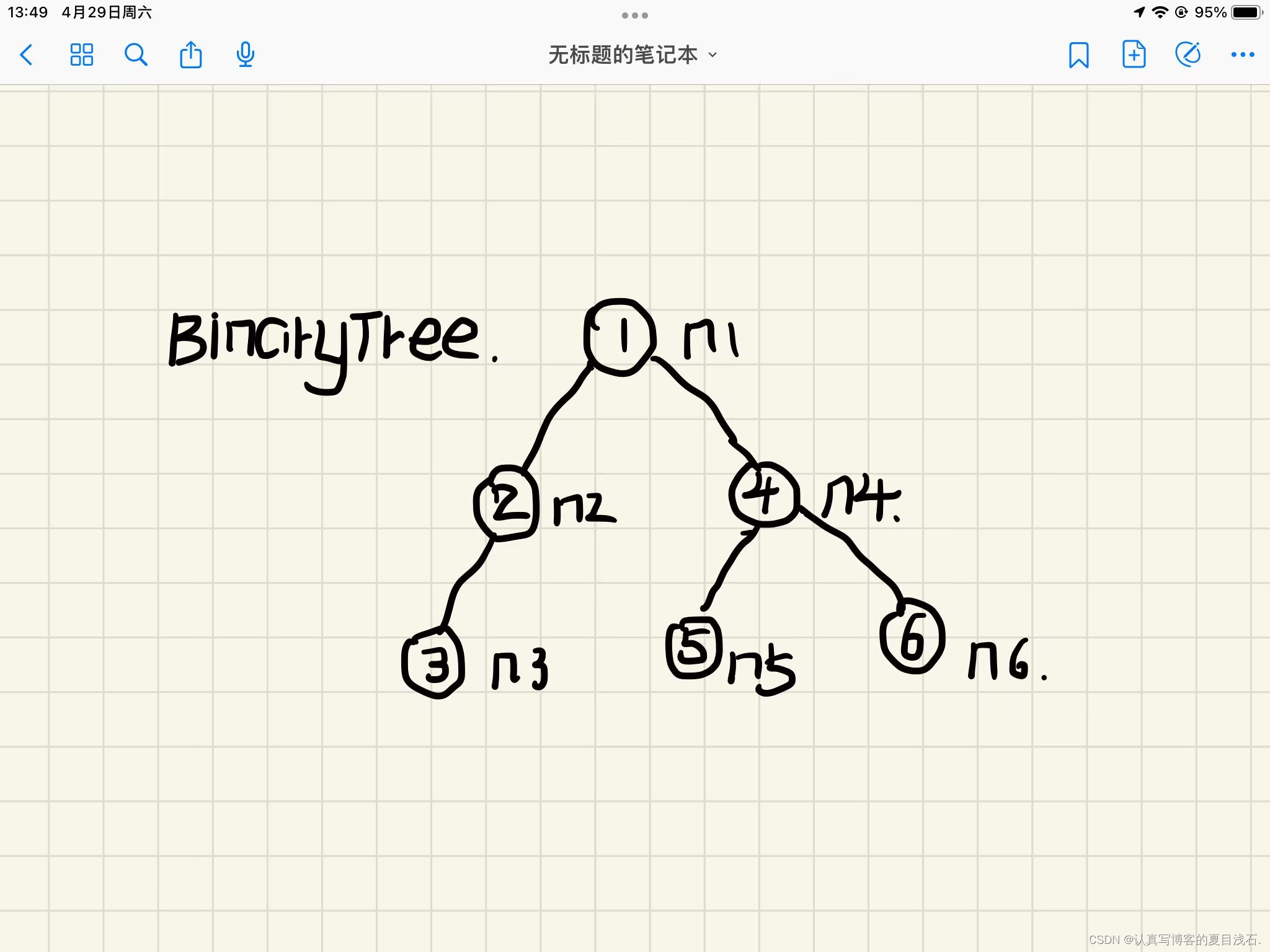
//创建节点
BTNode* BuyBTNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
return NULL;
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
void Test1()
{
// 构建二叉树
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
}
二叉树的前序遍历
前序遍历(Preorder Traversal 亦称先序遍历) —— 访问根结点的操作发生在遍历其左右子树之前。
由于被访问的结点必是某子树的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为根、根的左子树和根的右子树。所以 前序遍历 又可以被称为 NLR。
前序遍历图解:
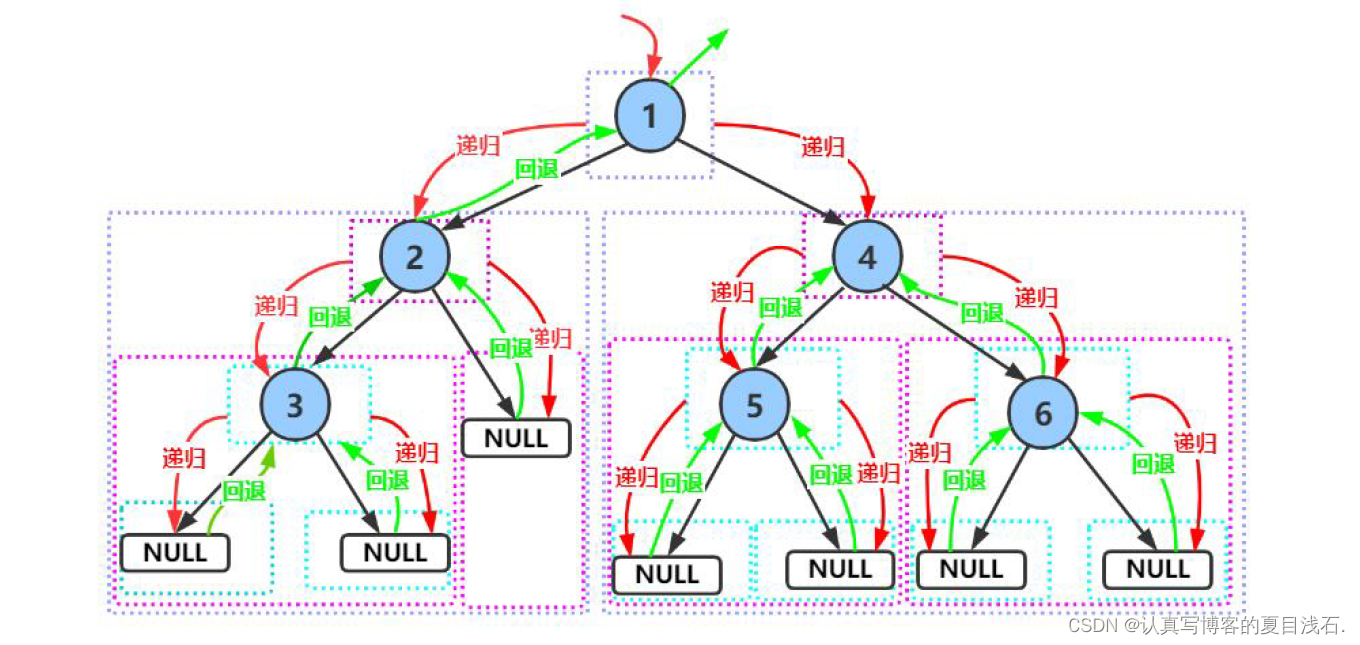
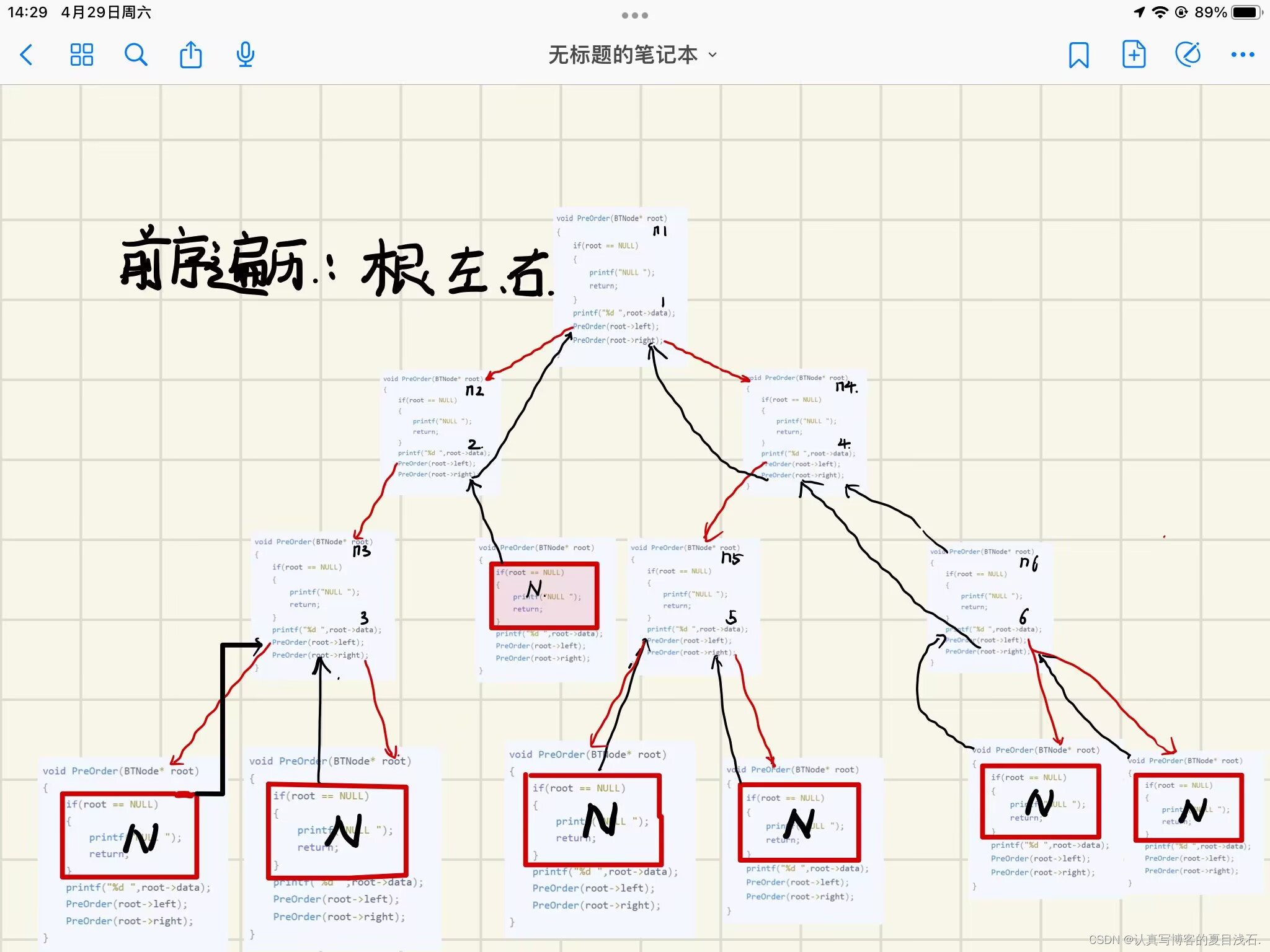
前序遍历的访问次序是 先访问根节点,再访问左子树,再访问右子树。
那么当前树的遍历结果为:1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
前序遍历的代码实现:
void PreOrder(BTNode* root)
{
if(root == NULL)
{
printf("NULL ");
return;
}
printf("%d ",root->data);
PreOrder(root->left);
PreOrder(root->right);
}
二叉树的中序遍历
中序遍历(Inorder Traversal) —— 访问根结点的操作发生在遍历其左右子树之中(间)。
中序遍历 又可以被称为 LNR。
中序遍历的访问次序是 先访问左子树,再访问根节点,再访问右子树。
那么当前树的遍历结果为:NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
中序遍历的代码实现:
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ",root->data);
InOrder(root->right);
}
二叉树的后序遍历
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
后序遍历 又可以被称为 LRN。
后序遍历的访问次序是 先访问左子树,再访问右子树,再访问根节点。
那么当前树的遍历结果为:NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
后序遍历的代码实现:
void PostOrder(BTNode* root)
{
if(root==NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ",root->data);
}
二叉树的层序遍历
序遍历就是从第一层开始从左向右逐个遍历。
那么当前树的遍历结果为:1 2 4 3 5 6
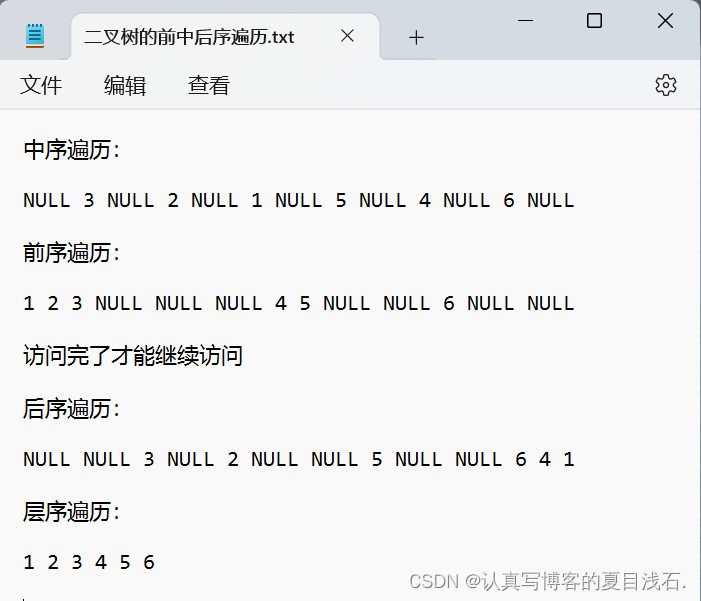
计算二叉树大小
计算二叉树的大小,其实就是计算二叉树中 节点的个数
思路:
1.给一个size,遍历二叉树,分别遍历左右子树,遍历过程中遍历到非空节点size++,遍历到空,则返回0。
2.二叉树的大小 = 根节点 + 左子树节点+右子树节点,将其分成多个子问题,递归求解。
思路1的实现:
当size是局部变量的时候,显然是不可以的!我们遍历的过程还是递归,当每次递归的时候,都会建立新的函数栈帧,递归当中的size不是同一个size,每次递归时的size一开始都是0,无法成功计算出大小。
所以这时候,我们需要设置一个全局变量的size,但是size不会被销毁,所以每一次计算二叉树大小的时候,就要重新初始化size的大小为0,避免计算错误。
思路一的代码实现:
int size=0;
int TreeSize1(BTNode* root)
{
if (root==NULL)
{
return 0;
}
size++;
TreeSize1(root->left);
TreeSize1(root->right);
return size;
}
思路1每次调用之前置0都很麻烦,代码也不是那么简洁,那么 思路2 能否改良这些?
显然思路2正能解决这两个缺陷
如果访问节点为空,则返回0;如果访问节点不为空,则 +1返回,就这样分别递归左子树和右子树,最后的返回结果就是节点个数。
思路二的代码实现:
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1;
}
计算叶子节点个数
叶子节点,就是没有左右孩子的节点。
如果节点为空,那么不是叶子结点,返回0;如果左右孩子都为空,那么就是叶子结点,返回1。
最后分别递归计算左右子树的叶子结点。
int TreeLeafSize(BTNode* root)
{
if(root == NULL)
return 0;
if(root->left==NULL && root->right == NULL)
return 1;
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
计算二叉树高度
二叉树的高度就是二叉树左右子树中最高的一边加上当前 1(根节点)。
我们可以分别递归到左右子树的最后一层,如果当前节点为空,返回0;不为空则比较当前左右子树的高度,+1返回高度较高的一边。
在递归过程中使用 leftHeight 和 rightHeight 分别记录当前高度,防止重复递归调用。
计算二叉树高度代码的实现:
int TreeHeight(BTNode* root)
{
if(root==NULL)
{
return 0;
}
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
计算第K层的节点个数
假设 k 足够大:
对于第一层,需要计算的是 第 k 层的节点个数;
对于第二层,需要计算的是 第 k - 1 层的节点个数;
… … … … … …
对于第 k 层,计算的就是 第 1 层( 当前层数 ) 的节点个数。
那么有了这个思路,我们就可以解决当前这个接口:
如果 当前节点为空,则返回0;
如果 节点不为空,且 k == 1,那么说明已经到达第 k 层,返回1;
如果 节点不为空,且 k > 1,那么说明需要继续递归,分别递归左右子树的 第 k - 1 层。
计算第K层的节点个数代码实现:
int TreeLevalSize(BTNode* root, int k)
{
if (root == NULL) return 0;
if (k == 1) return 1;
return TreeLevalSize(root->left, k - 1) + TreeLevalSize(root->right, k - 1);
}
查找某个值对应的节点
如果查找节点为空,则返回空;如果找到了则返回当前节点。
否则就分别递归查找左右子树,在查找过程中可以用变量来保存查找的值,如果查找返回的结果非空,那么说明找到了,就返回结果;如果左右子树都没有找到,则返回空。
BTNode* TreeFind(BTNode* root, int x)
{
// 如果 root 为空,则返回空
if (root == NULL)
{
return NULL;
}
// 找到了
if (root->data == x)
{
return root;
}
// 递归左右子树
BTNode* ret1 = TreeFind(root->left, x);
// 如果左子树非空,则找到了,返回
if (ret1 != NULL)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if (ret2 != NULL)
return ret2;
// 到这里没找到,就得返回NULL
return NULL;
}
二叉树的销毁
销毁二叉树,我们使用 后序遍历 的思想销毁。
遍历到最后一层,先销毁左子树,再销毁右子树,如果遇到空指针,那么直接返回。
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
}
这里我们需要注意一下,由于传的是一级指针,所以改变形参并不影响实参。在调用处销毁后需要 置空,防止误用。
三、完整代码
test.c
#define _CRT_SECURE_NO_WARNINGS 1
#include <stdio.h>
#include <stdlib.h>
typedef int BTDataType;
typedef struct BinaryTreeNode
{
BTDataType data;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
#include "Queue.h"
BTNode* BuyBTNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->left = NULL;
newnode->right = NULL;
return newnode;
}
// 前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
printf("%d ", root->data);
PreOrder(root->left);
PreOrder(root->right);
}
// 二叉树中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
// 二叉树后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PostOrder(root->left);
PostOrder(root->right);
printf("%d ", root->data);
}
// 计算二叉树大小
int size = 0;
int TreeSize1(BTNode* root)
{
if (root == NULL)
{
return 0;
}
size++;
TreeSize1(root->left);
TreeSize1(root->right);
return size;
}
int TreeSize2(BTNode* root)
{
return root == NULL ? 0 : TreeSize2(root->left) + TreeSize2(root->right) + 1;
}
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
// 层序遍历
//void LevelOrder(BTNode* root)
//{
// Queue q;
// QueueInit(&q);
//
// // 如果根非空,则入队列
// if (root != NULL)
// {
// QueuePush(&q, root);
// }
//
// // 队列非空则进行遍历
// while (!QueueEmpty(&q))
// {
// BTNode* front = QueueFront(&q);
// printf("%d ", front->data);
// QueuePop(&q);
//
// // 非空入队列
// if (front->left)
// {
// QueuePush(&q, front->left);
// }
//
// if (front->right)
// {
// QueuePush(&q, front->right);
// }
// }
//
// printf("\n");
// QueueDestroy(&q);
//}
// 控制一下层序遍历一层一层出
void LevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
// 如果根非空,则入队列
if (root != NULL)
{
QueuePush(&q, root);
}
// 算出每层的大小
int levelSize = QueueSize(&q);
// 不为空,则继续
while (!QueueEmpty(&q))
{
// 如果一层不为空,则继续出
while (levelSize--)
{
BTNode* front = QueueFront(&q);
printf("%d ", front->data);
QueuePop(&q);
// 非空入队列
if (front->left)
{
QueuePush(&q, front->left);
}
if (front->right)
{
QueuePush(&q, front->right);
}
}
printf("\n");
levelSize = QueueSize(&q);
}
printf("\n");
QueueDestroy(&q);
}
int TreeKLevelSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
if (k > 1)
{
return TreeKLevelSize(root->left, k - 1) + TreeKLevelSize(root->right, k - 1);
}
}
BTNode* TreeFind(BTNode* root, int x)
{
// 如果 root 为空,则返回空
if (root == NULL)
{
return NULL;
}
// 找到了
if (root->data == x)
{
return root;
}
// 否则递归左右子树
BTNode* ret1 = TreeFind(root->left, x);
// 如果左子树非空,则找到了,返回
if (ret1 != NULL)
return ret1;
BTNode* ret2 = TreeFind(root->right, x);
if (ret2 != NULL)
return ret2;
// 到这里没找到,就得返回NULL
return NULL;
}
// 判断二叉树是否是完全二叉树
bool TreeComplete(BTNode* root)
{
// 使用层序遍历思想
Queue q;
QueueInit(&q);
// 如果非空,则入队列
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
// 一旦出队列到空,就出去判断
if (front == NULL)
{
break;
}
else
{
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
}
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
if (front != NULL)
{
QueueDestroy(&q);
return false;
}
else
{
QueuePop(&q);
}
}
QueueDestroy(&q);
return true;
}
// 销毁
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
}
void TestBTree1()
{
// 构建二叉树
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
PreOrder(n1);
printf("\n");
InOrder(n1);
printf("\n");
PostOrder(n1);
printf("\n");
}
void TestBTree2()
{
// 构建二叉树
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
BTNode* n7 = BuyBTNode(7);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
n2->right = n7;
/*size = 0;
printf("%d\n", TreeSize1(n1));
size = 0;
printf("%d\n", TreeSize1(n1));
size = 0;
printf("%d\n", TreeSize1(n1));
printf("%d\n", TreeSize2(n1));
printf("%d\n", TreeLeafSize(n1));
printf("%d\n", TreeHeight(n1));
printf("%d\n", TreeKLevelSize(n1, 3));*/
printf("%d\n", TreeComplete(n1));
LevelOrder(n1);
TreeDestroy(n1);
n1 = NULL;
}
int main()
{
//TestBTree1();
TestBTree2();
return 0;
}