【拓扑排序】课程表系列
文章目录
- 课程表(环检测算法)
- 1. DFS
- 2. BFS
- 课程表 II(拓扑序列)
- 1. DFS
- 2. BFS
- 课程表 IV(记忆化搜索)
- 1. DFS
- 2. BFS
课程表(环检测算法)

1. DFS
先修课程之间的关系可以用有向图表示,用哈希表存储邻接表,很显然,当有向图成环时无法完成所有的课程

环检测算法需要使用两个数组,分别是 visited 和 path,visited数组用来记录遍历过的节点,而path用于记录正在遍历的路径且没有回溯到的节点。如果遍历某条支路时又到达某path数组记录为true的节点,说明成环了
比如上图中,根据dfs,从0出发后会遍历到1、3,然后会遍历2(visited[2]=true、path[2]=true),遍历3(visited[3]=true、path[3]=true),遍历4(visited[4]=true、path[4]=true),遍历2,然而此时发现path[2]=true,出现环!
下图描述了遍历的过程,在 visited 中被标记为 true 的节点用灰色表示,在 path 中被标记为 true 的节点用绿色表示
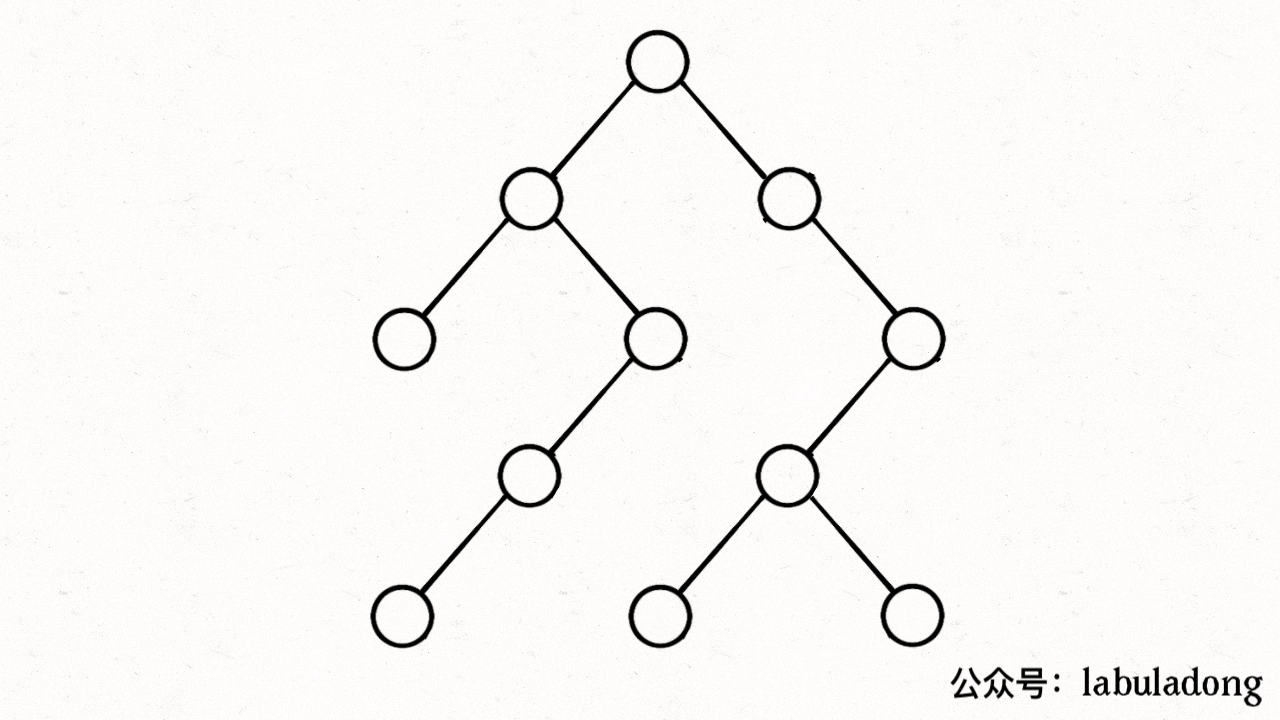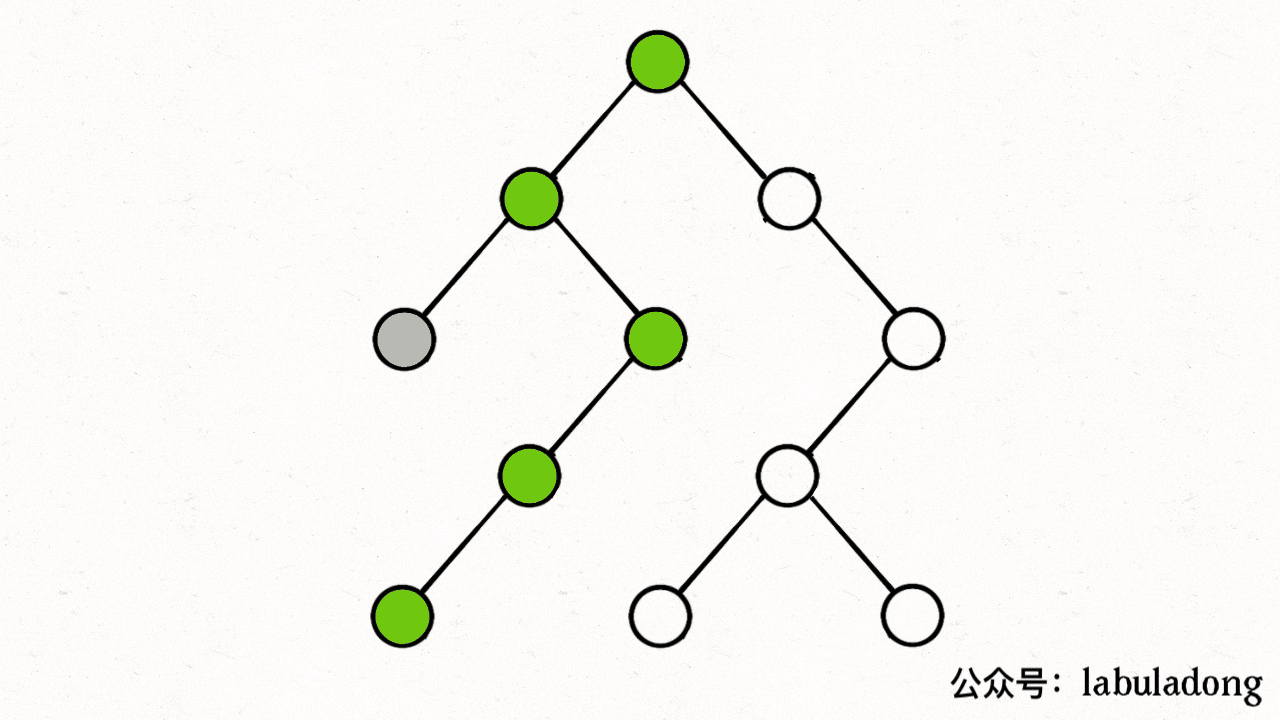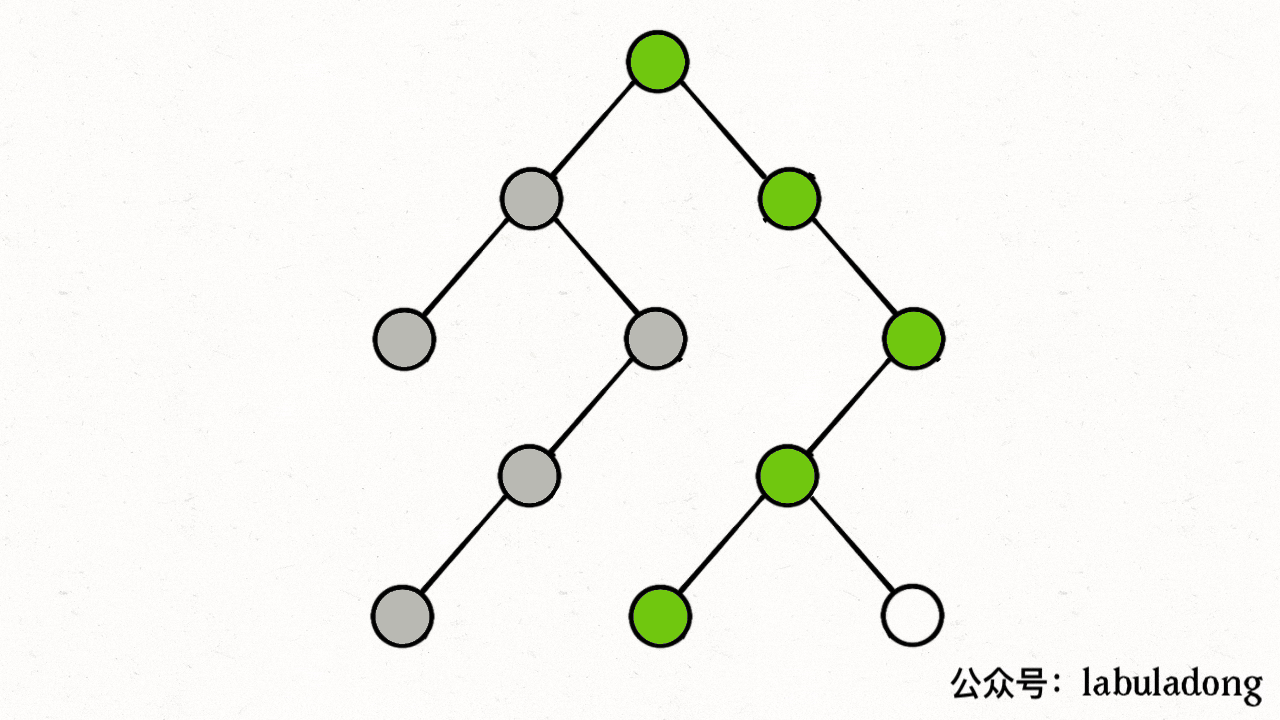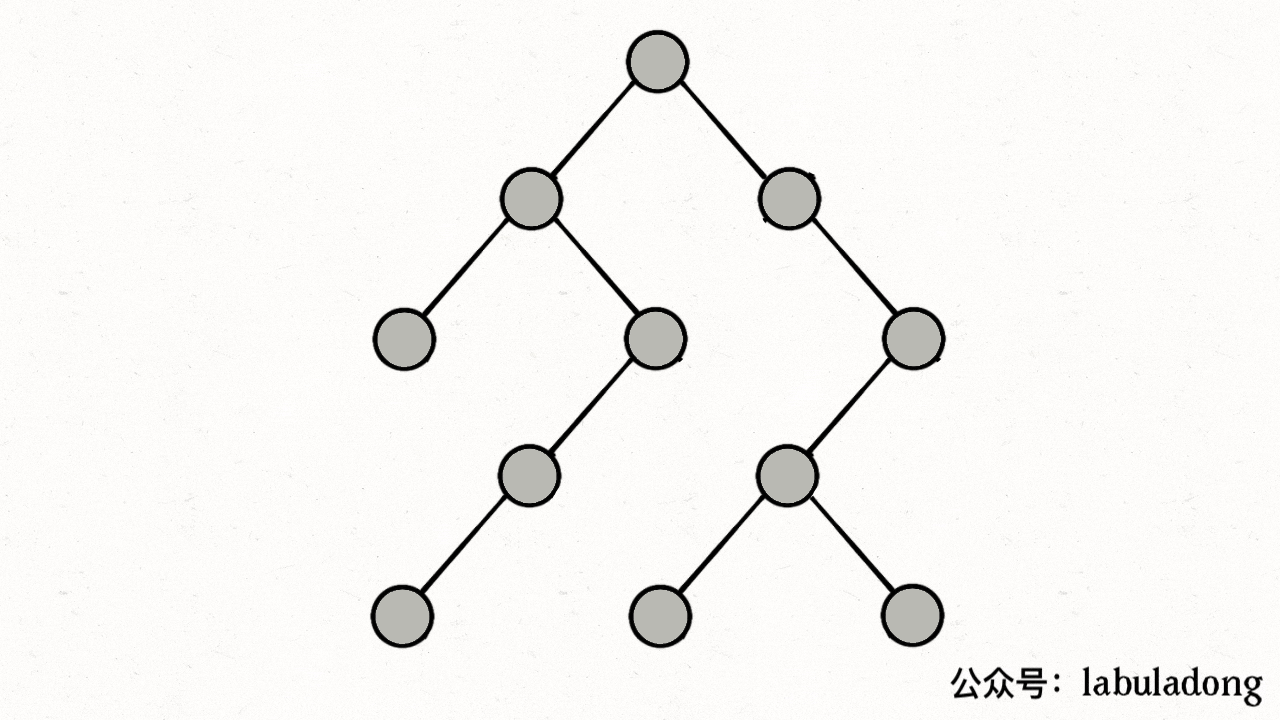
图源
class Solution {
public:
unordered_map<int, vector<int>> mp;
vector<bool> visited;
vector<bool> path;
bool valid;
void dfs(int start){
if(path[start]){
valid = false;
return;
}
if(visited[start]) return;
visited[start] = true;
path[start] = true;
for(int end : mp[start]){
// 判断条件不能是:valid && !visited[end],因为要检测环
if(valid) dfs(end);
}
path[start] = false;
}
bool canFinish(int n, vector<vector<int>>& prerequisites) {
visited.resize(n, false);
path.resize(n, false);
valid = true;
for(auto end_start : prerequisites){
mp[end_start[1]].push_back(end_start[0]);
}
// 由于图不像树一样有根节点,图没有入口节点,需要使用for循环试探每一个节点
for(int i = 0; i < n; i++){
if(valid) dfs(i);
}
return valid;
}
};
2. BFS
BFS 算法的思路:
-
构建邻接表,数据结构为哈希表 + 数组,unordered_map<int, vector<int>>
-
构建一个 indegree 数组记录每个节点的入度,即 indegree[i] 记录节点 i 的入度
-
对 BFS 队列进行初始化,入度为0说明没有先修课程,将入度为 0 的节点首先入队
-
开始执行 BFS ,不断弹出队列中的节点(表示修完一门课),减少相邻节点的入度(表示先修课程 - 1),并将入度变为 0 的节点加入队列
-
如果最终所有节点都被遍历过(count 等于节点数),则说明不存在环,反之则说明存在环。
class Solution {
public:
bool canFinish(int n, vector<vector<int>>& prerequisites) {
unordered_map<int, vector<int>> mp;
vector<int> indegree(n, 0);
for(auto end_start : prerequisites){
indegree[end_start[0]]++;
mp[end_start[1]].push_back(end_start[0]);
}
queue<int> q;
// 入度为0,说明不需要依赖其他课程,优先遍历
// 先将入度为0的节点放入队列
for(int i = 0; i < n; i++){
if(indegree[i] == 0){
q.push(i);
}
}
vector<int> res;
while(!q.empty()){
int start = q.front();
q.pop();
res.push_back(start); // 出队顺序就是拓扑序
for(int end : mp[start]){
// 由于start课程已经修了,将end课程的入度 - 1,表示依赖的课程少一个
indegree[end]--;
if(indegree[end] == 0){
// 入度为0,说明end课程的先修课程全部学完,可以放入队列遍历
q.push(end);
}
}
}
return res.size() == n;
}
};
课程表 II(拓扑序列)

1. DFS
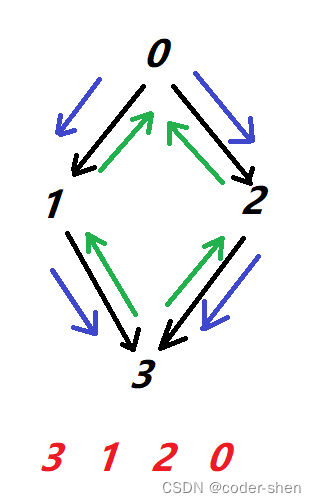
后序遍历反转就得到结果
class Solution {
public:
// 出现环,返回空数组,否则返回拓扑序
unordered_map<int, vector<int>> mp;
vector<bool> visited;
vector<bool> path;
vector<int> postorder;
bool valid;
void dfs(int start){
if(path[start]){
valid = false;
return;
}
if(visited[start]) return;
visited[start] = true;
path[start] = true;
for(int end : mp[start]){
if(valid) dfs(end);
}
path[start] = false;
postorder.push_back(start);
}
vector<int> findOrder(int n, vector<vector<int>>& prerequisites) {
visited.resize(n, false);
path.resize(n, false);
valid = true;
for(auto end_start : prerequisites){
mp[end_start[1]].push_back(end_start[0]);
}
for(int i = 0; i < n; i++){
if(valid) dfs(i);
}
if(!valid) return {};
reverse(postorder.begin(), postorder.end());
return postorder;
}
};
2. BFS
首先使用indegree数组记录每个节点的入度,将入度为0(表示没有先修课程)的节点放入队列,开始BFS
从队列中取出节点加入数组ans(拓扑序),将该节点能直达的节点end对应的indegree[end]减1,表示end的先修课程少了一门,如果indegree[end]为0,表示end对应的先修课程全部学完,可以加入队列遍历
遍历完后ans的长度若为n,则可以修完所有课程,否则有向图存在环,无法修完所有课程
class Solution {
public:
vector<int> findOrder(int n, vector<vector<int>>& prerequisites) {
unordered_map<int, vector<int>> mp;
vector<int> indegree(n, 0);
for(auto end_start : prerequisites){
indegree[end_start[0]]++;
mp[end_start[1]].push_back(end_start[0]);
}
queue<int> q;
// 入度为0,说明不需要依赖其他课程,优先遍历
// 先将入度为0的节点放入队列
for(int i = 0; i < n; i++){
if(indegree[i] == 0){
q.push(i);
}
}
vector<int> ans;
while(!q.empty()){
int start = q.front();
q.pop();
ans.push_back(start); // 出队顺序就是拓扑序
for(int end : mp[start]){
// 由于start课程已经修了,将end课程的入度 - 1,表示依赖的课程少一个
indegree[end]--;
if(indegree[end] == 0){
// 入度为0,说明end课程的先修课程全部学完,可以放入队列遍历
q.push(end);
}
}
}
if(ans.size() != n) return {};
return ans;
}
};
课程表 IV(记忆化搜索)
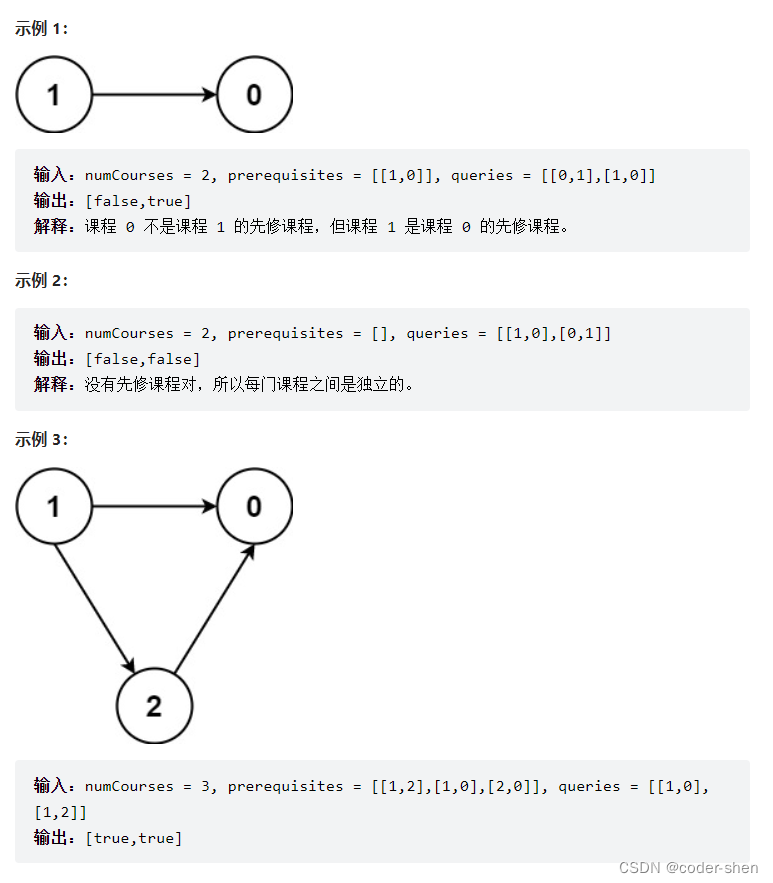
1. DFS
使用一个二维数组isReach表示start和end之间是否可达,其中1表示可达、-1表示不可达、0表示未定
搜索结果保存在二维数组isReach中,下一次搜索可以利用isReach数组
class Solution {
public:
unordered_map<int, vector<int>> mp;
vector<vector<int>> isReach; // 1表示可达、-1表示不可达、0表示未定
bool dfs(int start, int end){
if(isReach[start][end] == 1) return true;
if(isReach[start][end] == -1) return false;
for(int mid : mp[start]){
if(dfs(mid, end)){
isReach[start][end] = 1;
return true;
}
}
isReach[start][end] = -1;
return false;
}
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
isReach.resize(n, vector<int>(n, 0));
for(auto start_end : prerequisites){
mp[start_end[0]].push_back(start_end[1]);
isReach[start_end[0]][start_end[1]] = 1;
}
for(int i = 0; i < n; i++){
isReach[i][i] = 1;
}
vector<bool> ans;
for(auto q : queries){
ans.push_back(dfs(q[0], q[1]));
}
return ans;
}
};
2. BFS
每个节点都作为源点,把源点src加入队列中开始BFS,遍历到的所有节点mid,都将isReach[src][mid]都置为true
class Solution {
public:
unordered_map<int, vector<int>> mp;
vector<vector<int>> isReach;
bool bfs(int src, int end){
if(isReach[src][end] == 1) return true;
if(isReach[src][end] == -1) return false;
queue<int> q;
q.push(src);
while(!q.empty()){
int start = q.front();
q.pop();
for(int mid : mp[start]){
if(!isReach[src][mid]){
isReach[src][mid] = 1; // src -> start可达,start -> mid可达,则src -> mid可达
q.push(mid);
}
}
}
if(isReach[src][end] == 1) return true;
isReach[src][end] = -1; // 如果BFS遍历中,isReach[src][end]没被置为1,则说明不可达
return false;
}
vector<bool> checkIfPrerequisite(int n, vector<vector<int>>& prerequisites, vector<vector<int>>& queries) {
isReach.resize(n, vector<int>(n, 0));
for(auto start_end : prerequisites){
mp[start_end[0]].push_back(start_end[1]);
}
vector<bool> ans;
for(auto q : queries){
ans.push_back(bfs(q[0], q[1]));
}
return ans;
}
};
