DP动态规划
1.背包问题
1.1 0/1背包


1.1.1经典做法
def solve(N,C): # 从左到右,从上到下 (先种类,再体积)
for i in range(1,N+1): # N种物品,先1种,再2种......
for j in range(0,C+1): # 当前背包体积
if c[i]>j : dp[i][j] = dp[i-1][j]
else: dp[i][j] = max(dp[i-1][j-c[i]]+w[i],dp[i-1][j]) # 装或者不装,找最大值
return dp[N][C]
N,C= map(int,input().split())
n=3000
dp = [[0]*n for i in range(n)] # 初始化dp数组,预留更大空间
c=[0]*n # 记录体积
w=[0]*n # 记录价值
for i in range(1,N+1): #读入N种物品的价值和体积
c[i],w[i] = map(int,input().split())
print(solve(N,C))1.1.2 优化为两行队列存储

def solve(N,C): # 从左到右,从上到下 (先种类,再体积)
old = 1
new = 0
for i in range(1,N+1): # N种物品,先1种,再2种......
new,old = old,new # 交换两行
for j in range(0,C+1): # 当前背包体积
if c[i]>j : dp[new][j] = dp[old][j]
else: dp[new][j] = max(dp[old][j-c[i]]+w[i],dp[old][j]) # 装或者不装,找最大值
return dp[N][C]
N,C= map(int,input().split())
n=3000
dp = [[0]*n for i in range(2)] # 初始化dp数组,预留更大空间
c=[0]*n # 记录体积
w=[0]*n # 记录价值
for i in range(1,N+1): #读入N种物品的价值和体积
c[i],w[i] = map(int,input().split())
print(solve(N,C))1.1.3 优化为数组滚动
def solve(N,C): # 从左到右,从上到下 (先种类,再体积)
for i in range(1,N+1): # N种物品,先1种,再2种......
for j in range(C,c[i]-1,-1): # 当前背包体积,倒序进行,到c[i]-1,因为范围[c[i],C]
dp[j] = max(dp[j],dp[j-c[i]]+w[i]) # 选或者不选
return dp[C]
N,C= map(int,input().split())
n=3000
dp = [0]*n # 初始化dp数组,预留更大空间 一维
c=[0]*n # 记录体积
w=[0]*n # 记录价值
for i in range(1,N+1): #读入N种物品的价值和体积,从1开始计数
c[i],w[i] = map(int,input().split())
print(solve(N,C))1.2 0/1背包简化版
1.2.1 装箱问题

把体积看成最优化目标,即最大化体积
def solve(N,C): # 从左到右,从上到下 (先种类,再体积)
new = 0
old = 1
for i in range(1,N+1): # N种物品,先1种,再2种......
new,old = old,new
for j in range(0,C+1):
if c[i]>j: dp[new][j] = dp[old][j]
else: dp[new][j] = max(dp[old][j-c[i]]+c[i],dp[old][j])
return dp[N][C]
V = int(input()) # 体积
N = int(input()) # 物品种类
n=21000
dp = [[0]*n for i in range(2)] # 初始化dp数组,预留更大空间 一维
c=[0]*n # 记录体积
for i in range(1,N+1): #读入N种物品的价值和体积,从1开始计数
c[i]=int(input())
print(V-solve(N,V))数组滚动做法
def solve(N,C): # 从左到右,从上到下 (先种类,再体积)
for i in range(1,N+1): # N种物品,先1种,再2种......
for j in range(C,c[i]-1,-1): # 当前背包体积,倒序进行,到c[i]-1,因为范围[c[i],C]
dp[j] = max(dp[j],dp[j-c[i]]+c[i]) # 选或者不选
return dp[C]
V = int(input()) # 体积
N = int(input()) # 物品种类
n=21000
dp = [0]*n # 初始化dp数组,预留更大空间 一维
c=[0]*n # 记录体积
for i in range(1,N+1): #读入N种物品的价值和体积,从1开始计数
c[i]=int(input())
print(V-solve(N,V))1.2.2 0/1背包的方案数


# dp[i][j][k] 从数字1~i中取j个,和为k的方案数
dp = [[[0]*2222 for i in range(11)] for j in range(2222)]
for i in range (0,2023): # 初始化
dp[i][0][0]=1
for i in range(1,2023):
for j in range(1,11):
for k in range (1,2023):
if k<i: # 取不到i
dp[i][j][k] = dp[i-1][j][k]
else: # 没有取i + 取i的情况
dp[i][j][k]=dp[i-1][j][k]+dp[i-1][j-1][k-1]
print(dp[2022][10][2022])用滚动数组
# dp[i][j][k] 从数字1~i中取j个,和为k的方案数
dp = [[0]*2222 for i in range(11)]
dp[0][0]=1
for i in range(1,2023):
for j in range(10,0,-1): #10个数
for k in range(i,2023): # 只考虑k>i的情况,k<i的情况直接不变
dp[j][k]+=dp[j-1][k-1]
print(dp[10][2022])1.3 完全背包
CSDN优质文章讲解背包问题


# 代码与0/1背包相似,多了一个k循环用来遍历每种物品拿几个
# dp[i][j] 把前i种物品装入容量为j的背包所获得的最大价值
def solve(n, C): # 从左到右,从上到下 (先种类,再体积)
for i in range(1, n + 1): # N种物品,先1种,再2种......
for j in range(0, C + 1):
# if i==1:
# dp[i][j]=0
# else:
# dp[i][j]=dp[i-1][j]
# for k in range(0, j // c[i] + 1): # k * c[i] <=j # 在容量为j的背包中放k个
# dp[i][j] = max(dp[i][j], dp[i-1][j - k * c[i]] + k * w[i])
dp[i][j] = dp[i - 1][j]
if j > c[i]: # 看装几个可以获得最大价值
for k in range(0, j // c[i] + 1): # k * c[i] <=j # 在容量为j的背包中放k个
dp[i][j] = max(dp[i][j], dp[i - 1][j - k * c[i]] + k * w[i])
return dp[N][C]
N=3011
dp=[[0]*N for j in range(N) ]
w=[0]*N
c=[0]*N
n,C=map(int,input().split())
for i in range(1,n+1):
c[i],w[i]=map(int,input().split())
print(solve(n,C))1.4 分组背包
思路为0/1背包,完全背包的结合,三重循环

# 状态转移方程 dp[i][j] = max{dp[i-1][j] , dp[i-1][j-c[i][k]]+w[i][k] }
# 滚动数组 dp[j]=max{dp[j] , dp[j-c[i][k]]+w[i][k] }
dp=[0]*N
for i in range(1,n+1): # 遍历每个组
for j in range(C,-1,-1) : # 遍历每个容量
for k in range(1,C+1): # 用k枚举第i组的所有物品
if (j>=c[i][k]): # 第k个物品能够转入容量为j的背包
dp[j]=max( dp[j] , dp[j-c[i][k]] + w[i][k] ) # 不装 或者装 第i组第k个
print(dp[C])1.5 多重背包

1.5.1 转为0/1背包问题

1.5.2 转为与完全背包相似的问题


2. 线性DP
2.1 最长公共子序列


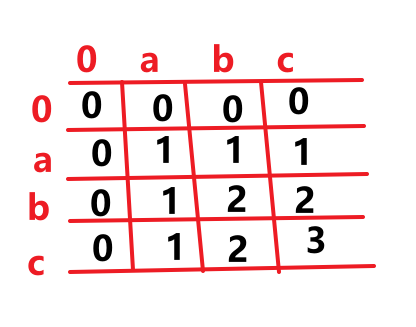
# 当 ai=bj 时,状态转移方程 dp[i][j] = dp[i-1][j-1] +1
# 当 ai!=bj时,状态转移方程 dp[i][j] = max{ dp[i][j-1] , dp[i-1][j]}
n,m = map(int,input().split()) # B n个元素 A m个元素
a = [0] + list(map(int,input().split()))
b = [0] + list(map(int,input().split()))
dp = [[0]*(m+1) for _ in range(2)] # 注意这里是m,不是n,进行初始化
now = 0 ;old = 1
for i in range(1,n+1): # B的长度1-n遍历
now,old = old,now
for j in range(1,m+1): # A的长度 1-m遍历
dp[now][j] = max(dp[now][j-1],dp[old][j]) #继承以前的最大值
if a[i]==b[j]:
dp[now][j] = dp[now][j]+1
print(dp[now][m])2.2 最长递增子序列 LIS



N =int(input()) # 对手个数
a = [0]+[int(i) for i in input().split()] # 记录对手战力值
dp = [0]*(N+1) # 记录以第i个数为结尾的最长递增子序列
dp[1]=1
for i in range(2,N+1): # 从2-N循环
for j in range(1,i): # 查找前面的比a[i]小的
if a[j]<a[i] and dp[j]>dp[i]: #找到小的同时给他赋值max(dp[j])
dp[i]=dp[j]
dp[i]+=1 # 加1,即本身
max(dp)2.3 编辑距离,字符串转换


"""
A转换为B
删除: A删除最后一个 dp[i][j]=dp[i-1][j]+1
插入: B末尾插入相同的 dp[i][j]=dp[i][j-1]+1
替换: A的末尾直接替换 dp[i][j]=dp[i-1][j-1]+1
"""
# dp[i][j] 表示A的前i个字符转换B的前j个字符所需要的操作步骤
# 将长度为m的A存储在a[1]~a[m]中,不用a[0]和b[0]
"""转移方程"""
# a[i]=b[j],则dp[i][j] = dp[i-1][j-1]
# 其他情况 dp[i][j] = min{dp[i-1][j-1], dp[i-1][j],dp[i][j-1]} +1
a=' '+input()
b=" "+input()
m=len(a)-1
n=len(b)-1
dp = [[0]*(n+1) for i in range(m+1)]
for i in range(1,m+1):dp[i][0]=i
for j in range(1,n+1):dp[0][j]=j
for i in range(1,m+1): # 遍历a的每一个
for j in range(1,n+1): # 遍历b的每一个
if a[i]==b[j]:
dp[i][j]=dp[i-1][j-1]
else:
dp[i][j]=min([dp[i-1][j],dp[i][j-1],dp[i-1][j-1]])+1
print(dp[m][n])2.3.1网格上的DP(过河卒)
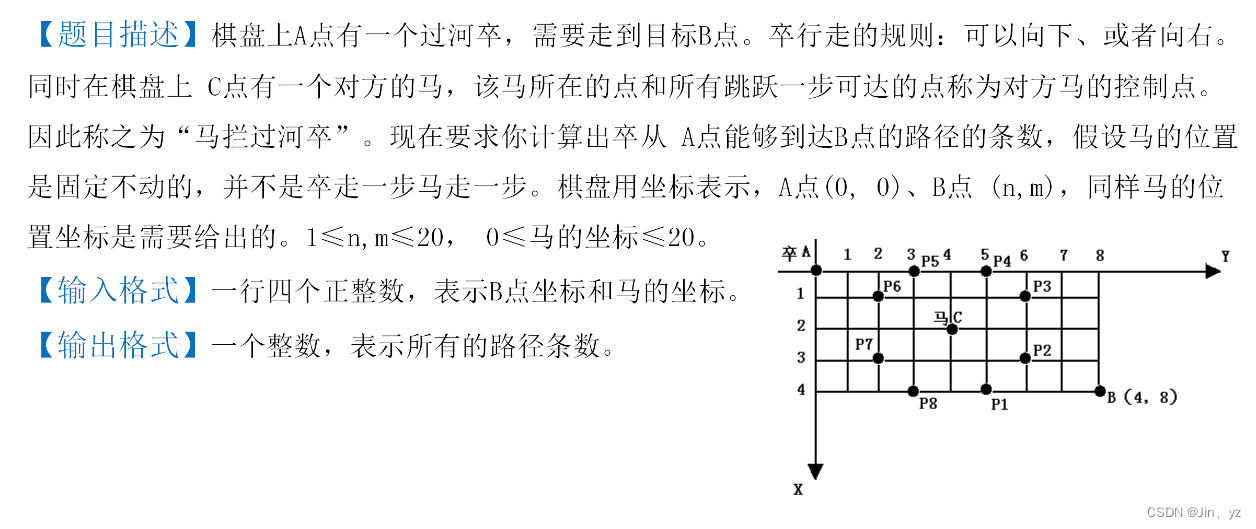
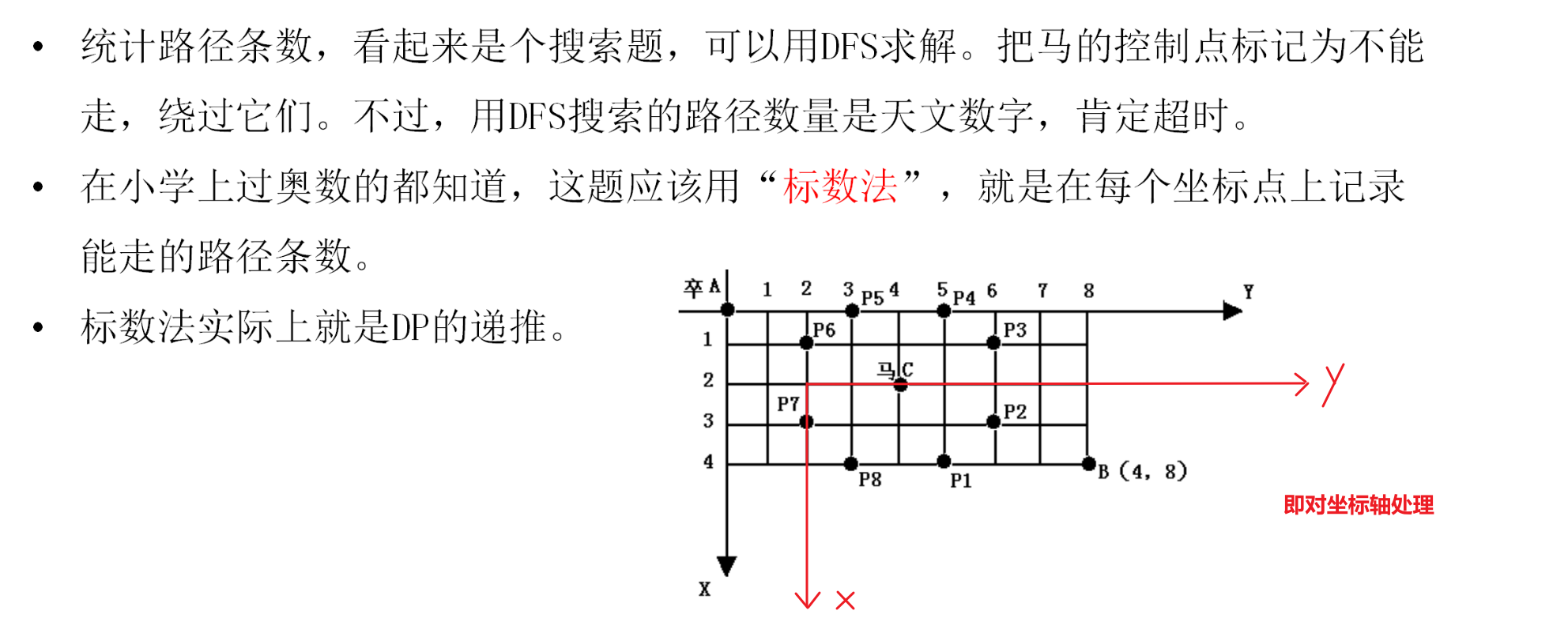

x1,y1,x2,y2 = map(int,input().split()) # B点坐标和马的坐标
dp = [[0]*25 for i in range(25)]
s = [[0]*25 for i in range(25)]
x1+=2;y1+=2;x2+=2;y2+=2 # 相当于从(2,2)开始的,坐标轴左移2,右移动2
dp[2][1] = 1 # 初始化,也可以 dp[1][2]=1
# 将马可到达的点全部置为1,即不可达
s[x2][y2]=1
s[x2-2][y2-1]=1;s[x2-2][y2+1]=1;s[x2+2][y2-1]=1;s[x2+2][y2+1]=1;
s[x2-1][y2-2]=1;s[x2-1][y2+2]=1;s[x2+1][y2-2]=1;s[x2+1][y2+2]=1;
for i in range(2,x2+1):
for j in range(2,y2+1):
if s[i][j]==1:
dp[i][j]=0
else: dp[i][j] = dp[i-1][j]+dp[i][j-1] # 上面的路径加上左边的路径
print(dp[x1][y1])2.4 DP例题
2.4.1 排列数
暴力法,使用内置排列组合
from itertools import * # 导入itertools 使用排列函数 permutations(list)
n,k = map(int, input().split())
nums = [i for i in range (1, n+1)] #1~n
cnt = 0
for num in permutations (nums): #检查每个排列
tmp = 0 #记录有多少个折点
for i in range (n-2) :
if num[i+1]>num[i+2] and num[i+1]>num[i]:
tmp += 1 #凸折点
elif num[i+1]<num[i+2] and num[i+1]<num[i]:
tmp += 1 #凹折点
if tmp == k-1 : cnt+=1
print(cnt % 123456)
DP动态规划做法
2.4.2 数字三角形

n = int(input())
a = [list(map(int,input().split())) for i in range(n)]
# 数组a[][] 同时当成dp[][]用
# 从上到下遍历
for i in range(1,n): #循环n-1次
for j in range(0,i+1): # 第i层有i个元素
if j==0:
a[i][j]+=a[i-1][j]
elif j==i:
a[i][j]+=a[i-1][j-1]
else:
#a[i][j]=max(a[i-1][j-1],a[i-1][j])
a[i][j]+=max(a[i-1][j-1:j+1])
if n&1: #奇数,位运算
print(a[-1][n//2]) # 1 2 3 # 3//2=1
else:
print(max(a[-1][n//2-1],a[-1][n//2])) # 1 2 3 4 #4//2=23 状态压缩DP(Python考的概率很小)
3.1 含义和表示
结合位运算,通过二进制来表示有或者没有。

"""
<< 右移运算
a=1<<(n-1) 即右移n-1位
1<<2 100
通过或运算实现相加去重
temp |=(1<<(n-1))
1<<2 100
temp=10
temp |=(1<<2) 110
"""
"""
1<<(i-1) &a 判断第i为是否为1
a|(1<<(i-1)) 将第i为改为1
a&(a-1) 去掉最后一个1
快速幂需要借鉴位运算
"""3.2 状态DP例题糖果


例如有 2 3 5三种口味,可以用 10110 表示!

import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
n,m,k = map(int,input().split())
tot=(1<<m)-1 # tot: 二进制是m个1,表示所有m种口味
dp=[-1 for _ in range(1<<20)] # 全部初始化为-1,同时将大小设置大一点
dp[0]=0 #
kw = []
for _ in range(n): # 存糖果
kw.append([int(i) for i in input().split()])
for c in kw: # 遍历每一包糖果
temp=0
for x in c: #[ 2 ,3 ,4]
temp|=(1<<(x-1)) # 状态压缩
for i in range(tot+1): # 口味是从0-tot
if (dp[i]==-1): # 没有得到过该种口味,直接跳过
continue
newcase = temp| i # 得到新的口味
if (dp[newcase] ==-1 or (dp[newcase]>dp[i]+1)): # 找到更少的口味组合
dp[newcase]=dp[i]+1
print(dp[tot])
# 有点类似 Dijstra , SPFA , BEll_Floyd
3.3 矩阵计数例题


# 0 用0表示 X 用1表示
# 横,竖不能出现连续的3个1
# dp[i][j][k] 第i行的合法状态为j,前一行为k
def check(x):
num=0
while(x):
if x&1: num+=1 #发现一个1
else: num=0 #不是连续的重新计数
if num==3:
return False
x>>=1 # 右移一次
N,M = list(map(int,input().split()))
s=2**M
row =[]
for i in range(s): #可能的范围 0000-1111
if check(i):
row.append(i)
dp=[[[0 for k in range(s)] for j in ragne(s)] for k in range(N)]
for i in row:
dp[0][i][0]=1
for i in range(1,N): # 遍历每一行
for j in row: # 连续检测三列是否合法
for k in row:
for p in row:
if j&k&p==0:
dp[i][j][k]+=dp[i-1][k][p]
ans=0
for j in row:
ans+=sum(dp[N-1][j])
print(ans)3.4 回路计数例题(没看懂)



from math import gcd
m=1<<22
dp=[[0 for j in range(22)] for i in range(m)]
dist = [[False for j in range(22)] for i in range(22)] # 矩阵存图
for i in range(1,22):
for j in range(1,22):
if gcd(i,j)==1:
dist[i][j]=True
dist[2][1]=1
for S in range(2,m-1): # 10-111110
for j in range(1,22):
if S>>j&1:
for k in range(1,22):
if S-(1<<j)>>k &1 and dist[k][j]:
dp[S][j]+=dp[S-(1<<j)][k]
ans=0
for i in range(2,22):
ans+=dp[m-2][i]
print(ans)4 树形DP
DFS(不用vis数组)+ 树结构

4.1 生命之树



即要我们找最大子树
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
def dfs(u,fa):
global ans
for son in t[u]:
if son !=fa:
dfs(son,u) # 遍历搜索
if dp[son]>0: # 子节点大于0,父结点就添加
dp[u]+=dp[son]
ans=max(ans,dp[u])
n=int(input())
dp=[0]*(n+1)
dp[1:n]=map(int,input().split()) # 不用dp[0]
t=[[] for i in range(n+1)] # tree,临接表矩阵
for i in range(n-1): # 存n-1条边
u,v=map(int,input().split())
t[u].append(v) #记录邻居
t[v].append(u)
ans=0
dfs(1,-1)
print(ans)
#tt=[[]*10] 这样创建里面只有1个
#tt=[[] for i in range(10)]
4.2 大臣的旅费例题


两次DFS有贪心的思想,第一次DFS找到最远的,第二次一定找到最远的(不适合有负数的情况)
树形DP只要一次DFS


给出两种实现方式,要标记数组和不要标记数组,都是只遍历一次,保证不回头遍历
import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
##def dfs(u):
## global ans
## vis[u]=1 #标记为访问过
## for v,c in e[u]: # 遍历u的邻居v,费用c
## if vis[v]==1:
## continue
## dfs(v)
## ans = max(ans ,dp[u]+dp[v]+c)
## dp[u]=max(dp[u],dp[v]+c)
##
##n=int(input())
##e=[[] for i in range(n+1)] # 存图
##for i in range(n-1):
## a,b,c=map(int,input().split())
## e[a].append((b,c)) # 临接表存边
## e[b].append((a,c))
##
##ans=0
##vis=[0 for i in range(n+1)]
##dp=[0 for i in range(n+1)]
##dfs(1)
##print(ans*10 + ans*(ans+1)//2) # 等差数列求和
def dfs(u,fa):
global ans
for v,c in e[u]: # 遍历u的邻居v,费用c
if v!=fa:
dfs(v,u)
ans = max(ans ,dp[u]+dp[v]+c)
dp[u]=max(dp[u],dp[v]+c)
n=int(input())
e=[[] for i in range(n+1)] # 存图
for i in range(n-1):
a,b,c=map(int,input().split())
e[a].append((b,c)) # 临接表存边
e[b].append((a,c))
ans=0
dp=[0 for i in range(n+1)]
dfs(1,-1)
print(ans*10 + ans*(ans+1)//2) # 等差数列求和
5 数位DP
5.1 数位DP介绍

dp[ i ] :i位数的每种数码有多少个,将0也看成占位符,后期再特别处理。
例如一位数:0-9
两位数:00-99
三位数:000-999
dp[ i ] 的计算
递推计算

排列组合计算(总共10**i个数字,每个数字上面有i位,10个数均等出现)

5.2 统计所有数码的出现个数





import sys
import collections
import itertools
import heapq
sys.setrecursionlimit(300000)
def solve(x): #计算[1,x]中的每个数码的个数
n=tuple(map(int,str(x))) #把一个数按位分解 123 —> (1,2,3)
n=n[::-1] # (1,2,3)—> (3,2,1)
for i in range(len(n)-1,-1,-1): # 从高到低处理x的每一位 (2,1,0)
for j in range(10):
cnt[j]+=dp[i]*n[i]
for j in range(n[i]): # (1)特判最高位比n[i]小的数字
cnt[j]+=ten[i]
u=0
for j in range(i-1,-1,-1):
u=u*10+n[j]
cnt[n[i]]+=u+1 #(2)特判最高位的数字n[i],
cnt[0]-=ten[i] # 特判前导0 ,对前导0去除
ten=[0]*15
ten[0]=1 # ten[i] : 10的i次方
dp=[0]*15
for i in range(1,15): #预计算dp[]
# dp[i]=i*10**(i-1) 这个和下面一样,但是运算速度比下面慢
dp[i] = i*ten[i-1] # 或者dp[i]=dp[i-1]*10+ten[i-1]
ten[i]=ten[i-1]*10
b=int(input())
cnt=[0]*15 # 答案cnt[i] ,数字“i”出现了多少次
solve(b)
for i in range(10):
print(cnt[i],end=" ") # 打印每个数码出现的次数

