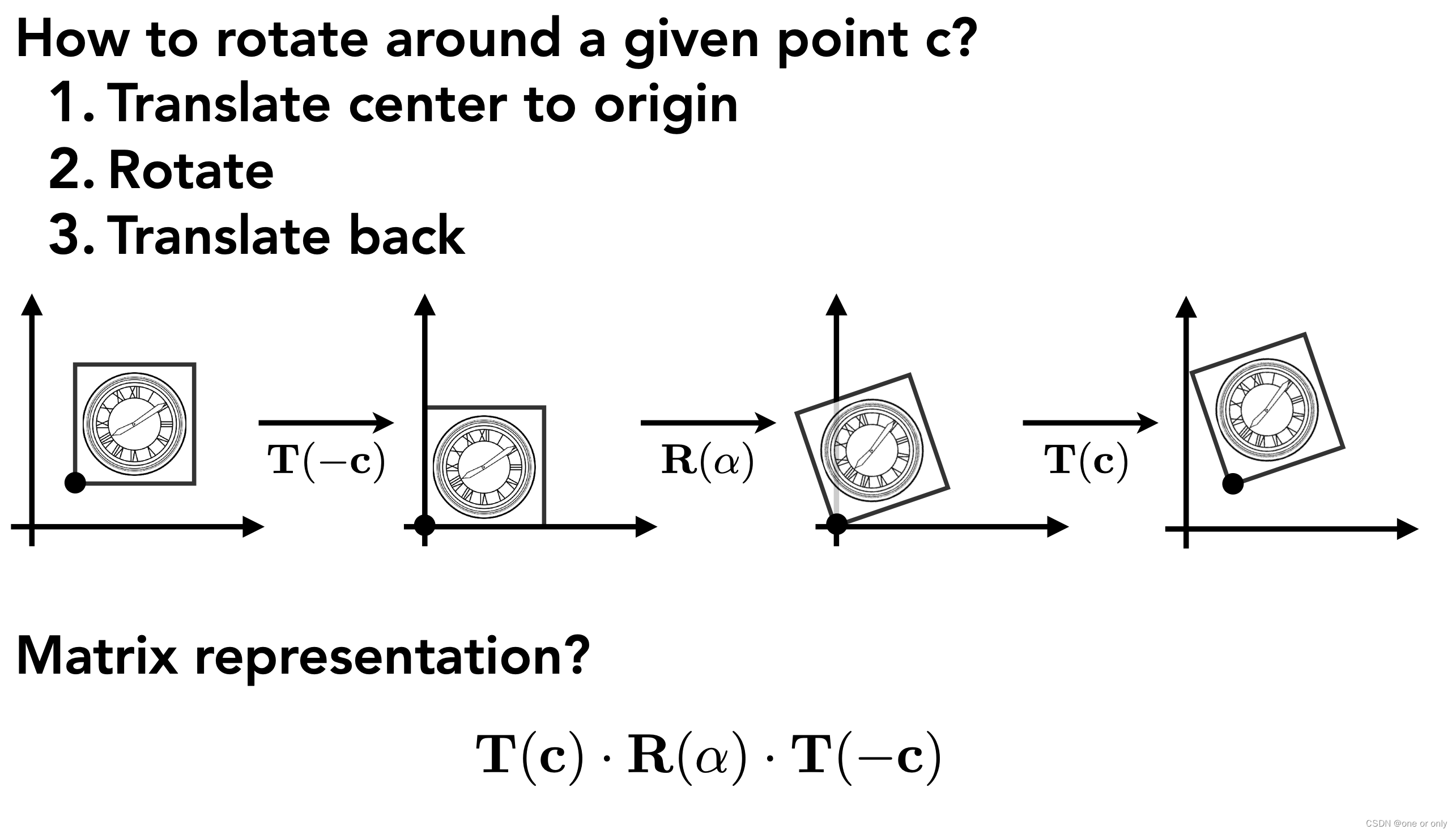
【GAMES101】03 Transformation
2D线性变换 ——写成矩阵形式
1、Scale(缩放)
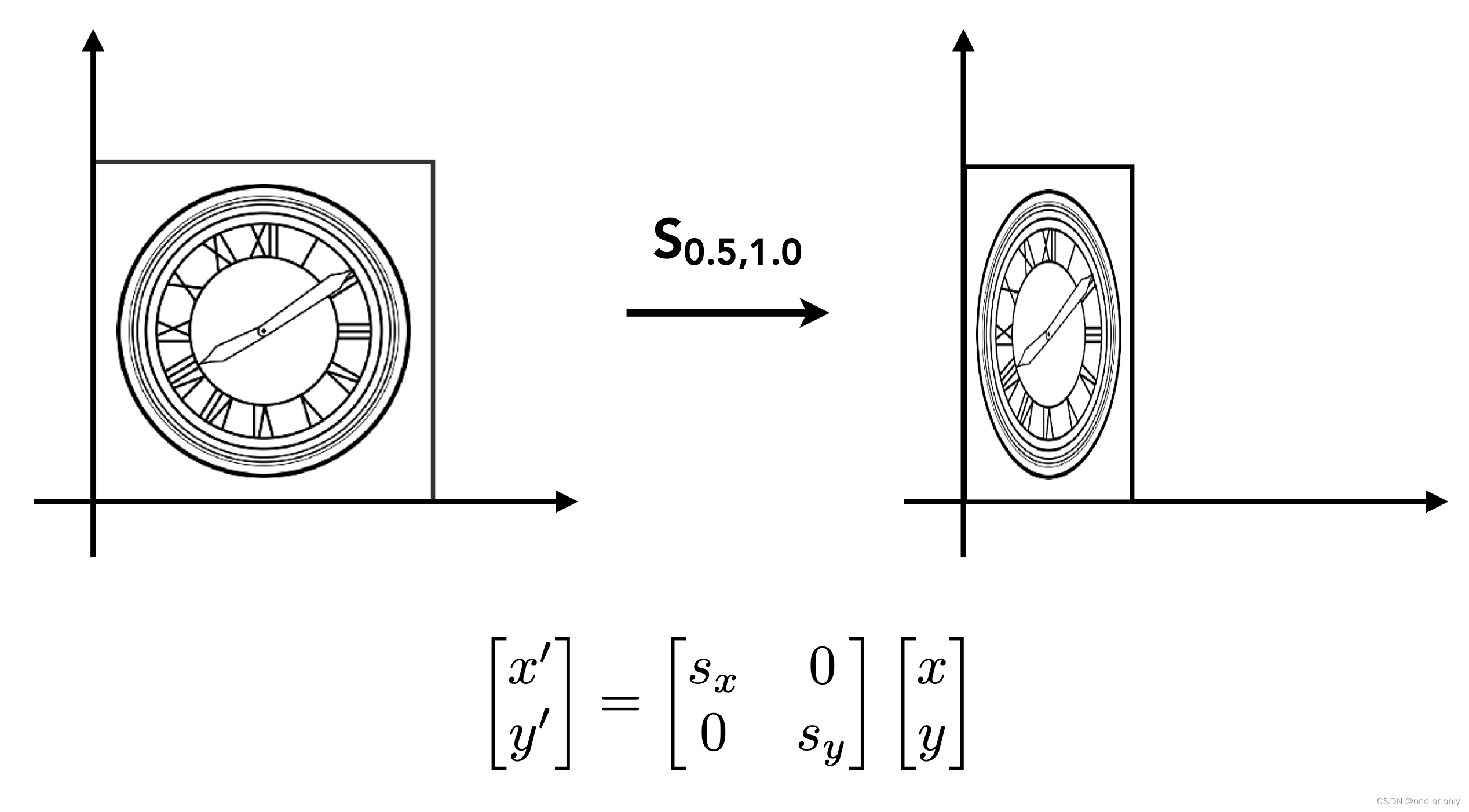
2、Reflection Matrix(反射矩阵)
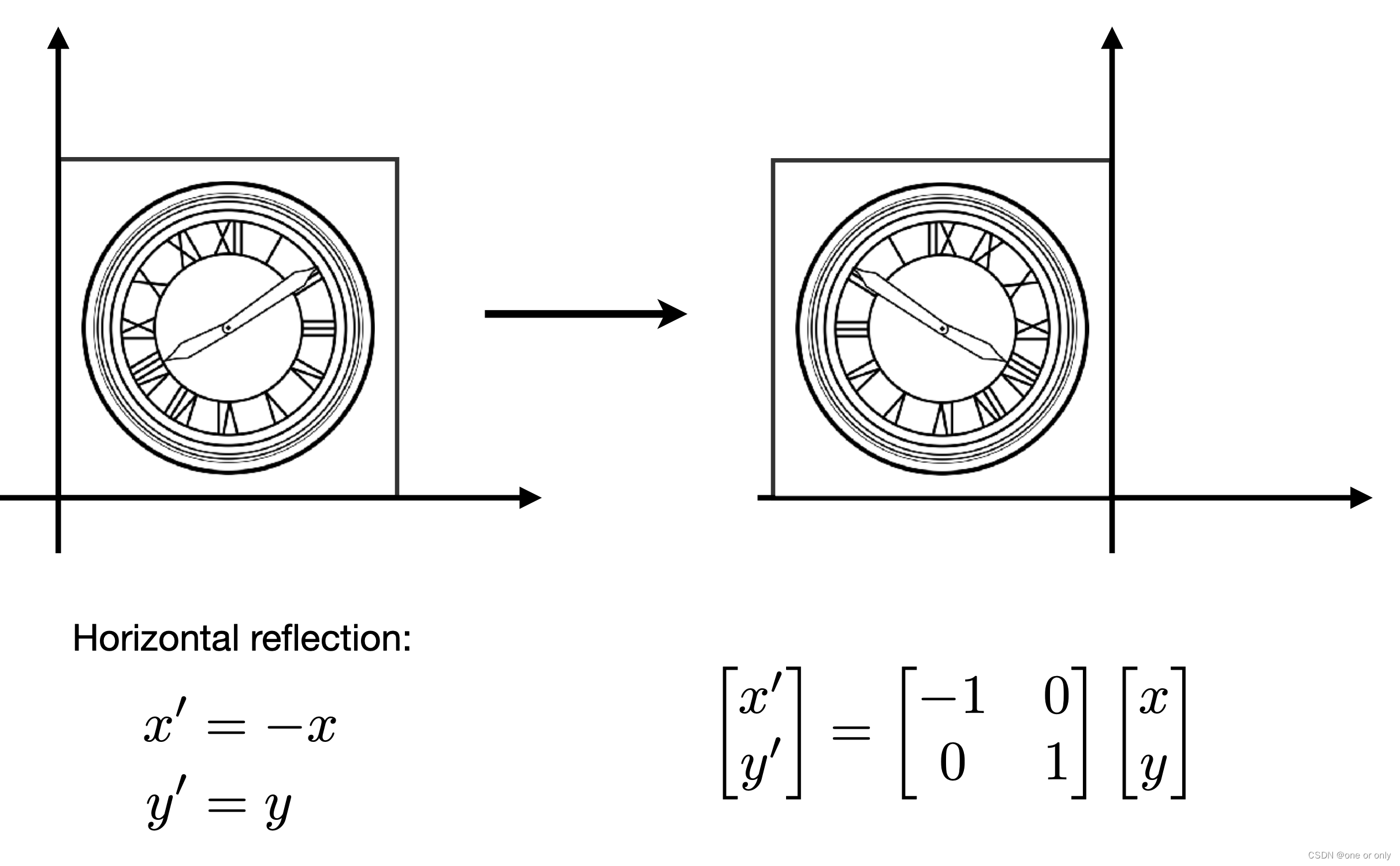
3、Shear Matrix(剪切矩阵)
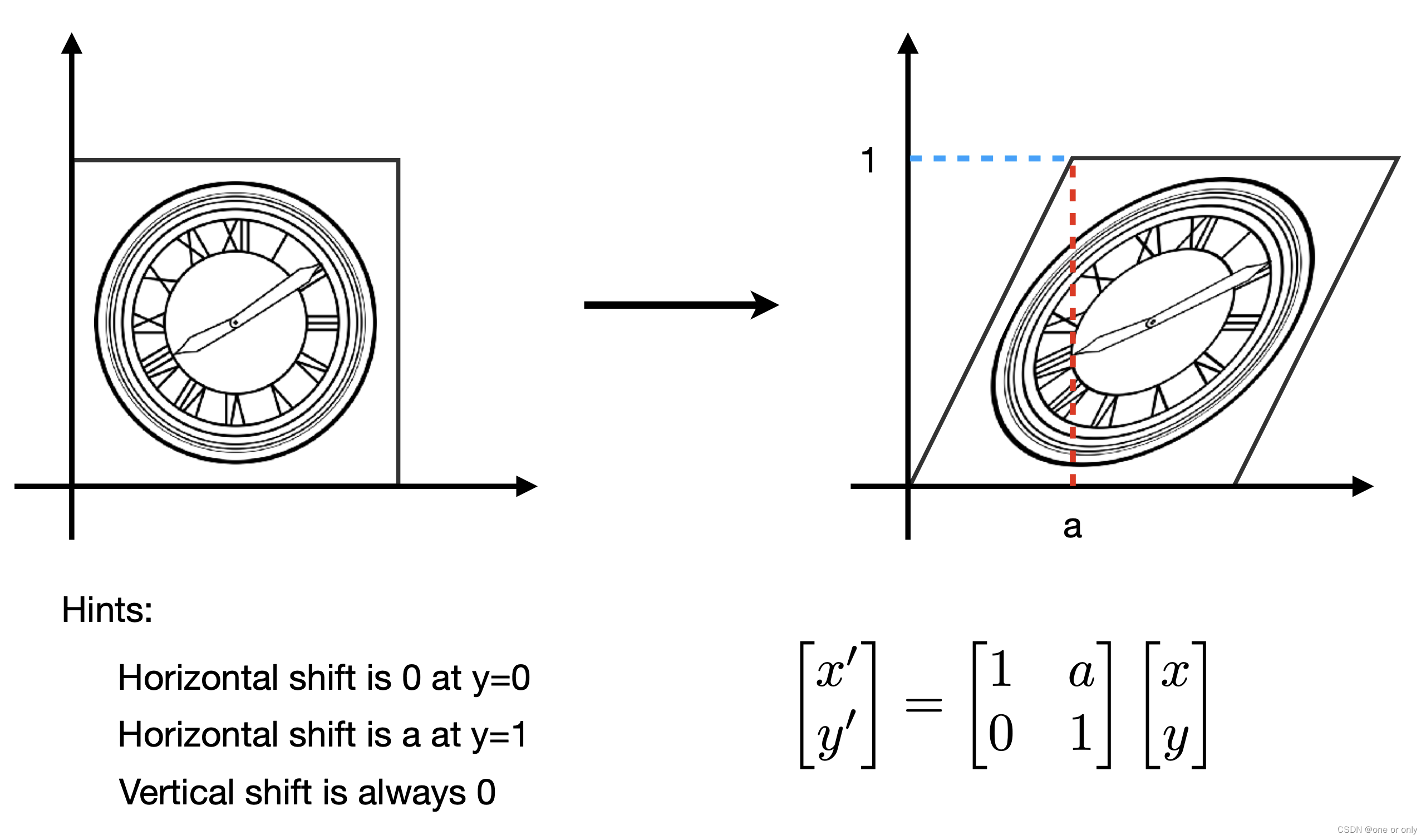
4、Rotation Matrix(旋转矩阵)
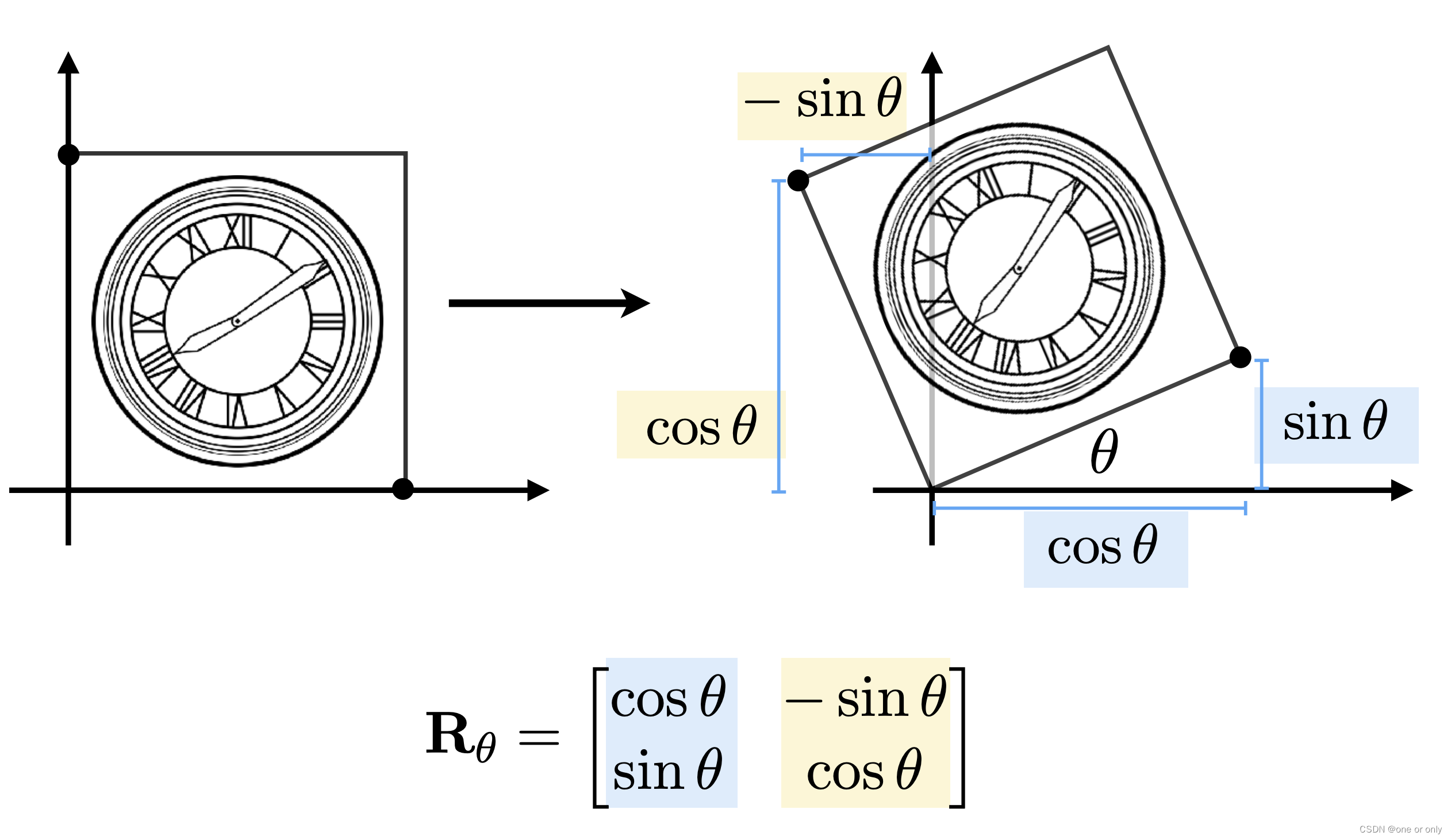
推导过程:
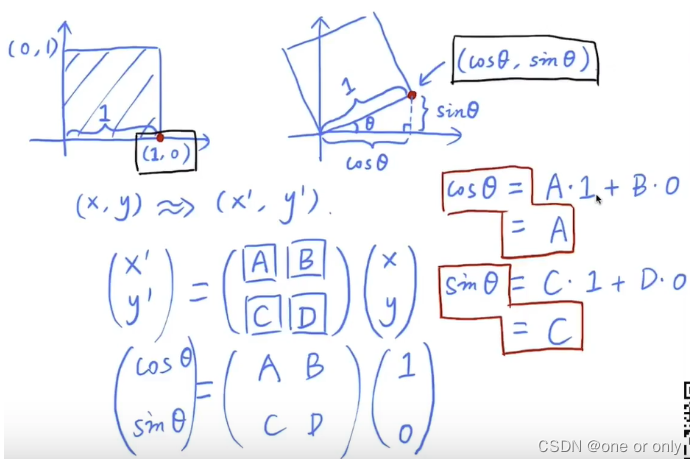
5、Translation Matrix(平移矩阵)
平移操作不属于线性变换的范畴。
引入齐次坐标,通过增加维度,来将平移坐标写成同样的矩阵形式。
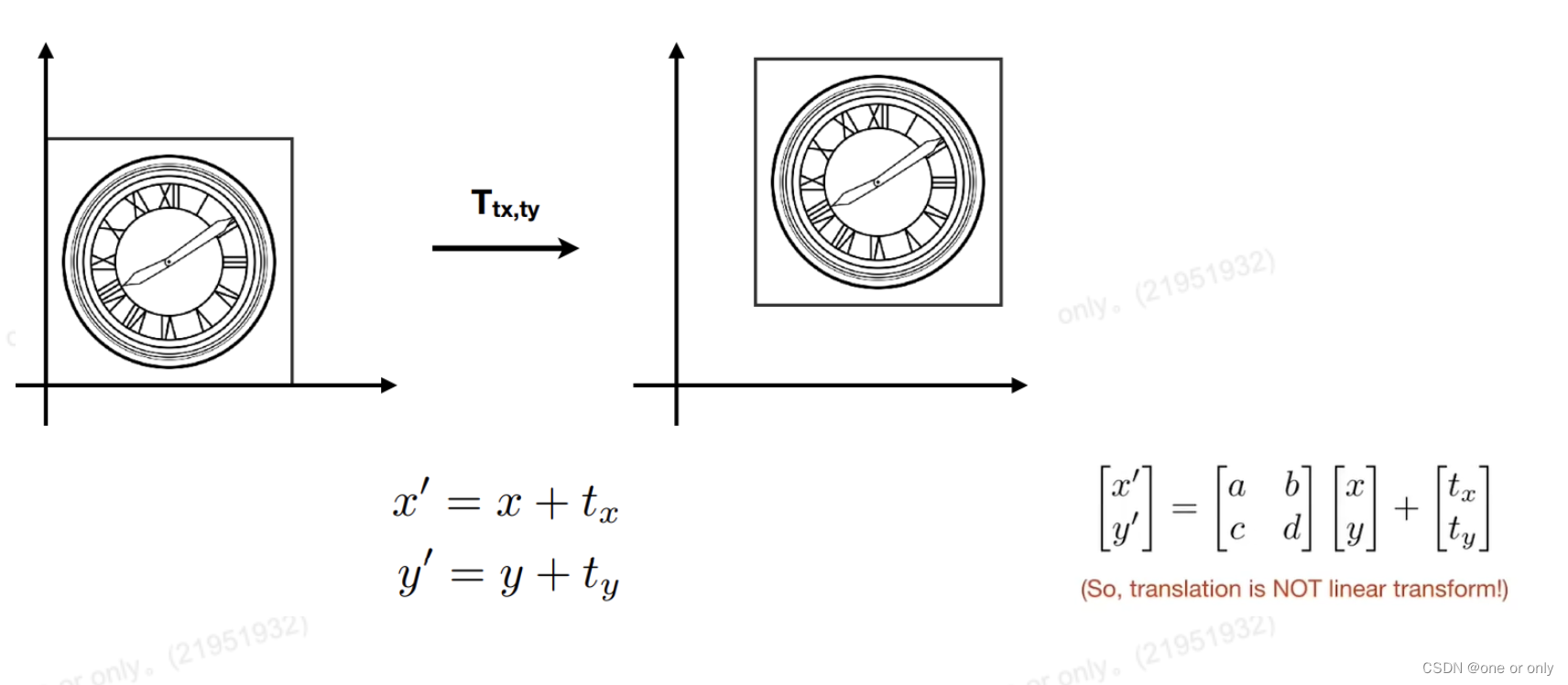
很显然,平移无法像上面的乘以某个矩阵,就等于结果。而是,加上某个矩阵。为了解决这个问题,引入齐次方程。就是新增一个额外的维度。用N+1维来表示N维坐标;把坐标统一转换为齐次坐标之后,就可以解决组合变换中存在平移时不能用矩阵连乘表示的问题了。

引入齐次坐标 使得用一种矩阵表示的形式统一了所有变换方式。

变换的顺序非常重要。
因为是列向量,所以运算顺序从右往左乘