leetcode刷题之有关树的算法

144.二叉树的前序遍历

方法一:递归

var preorderTraversal = function(root) {
    let arr = []
    const preorder = root =>{
        //递归的出口
        if(root==null){
            return
        }
        arr.push(root.val)
        preorder(root.left)
        preorder(root.right)
    }
    preorder(root)
    return arr
};

方法二：迭代 使用栈

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number[]}
         优秀是一种习惯                    迭代实现
 */
var preorderTraversal = function(root) {
    if(!root) return []
    let arr = []
    let stack = [root]
    while(stack.length){
        let node = stack.pop()
        arr.push(node.val)
        node.right&&stack.push(node.right)
        node.left&&stack.push(node.left)
    }
    return arr
};

94.二叉树的中序遍历

方法一：递归

var inorderTraversal = function(root) {
    //递归 
    let arr = []
    const inorder = root =>{
        if(!root) return []
        inorder(root.left)
        arr.push(root.val)
        inorder(root.right)
    }
    inorder(root)
    return arr
};

方法二：迭代

var inorderTraversal = function(root) {
    //迭代
    let arr = []
    let stack = []
    //也就是 root == null
    if(!root) return []
    //左节点一直入栈
    while(root){
        stack.push(root)
        root = root.left
    }
    //开始出栈
    while(stack.length){
        let node = stack.pop()
        arr.push(node.val)
        let temp = node.right
        //当前的结点出栈之后，检查其右侧结点的情况 依次入栈
        while(temp){
            stack.push(temp)
            temp = temp.left
        }
    }
    return arr
};

145.二叉树的后序遍历

方法一:递归

var postorderTraversal = function(root) {
    //递归
    let arr = []
    const postorder = root =>{
        //递归出去的条件
        if(!root) return 
        postorder(root.left)
        postorder(root.right)
        arr.push(root.val)
    }
    postorder(root)
    return arr
};

方法二：迭代 使用栈

var postorderTraversal = function(root) {
    //先将root的值放入到arr中，然后将root.right left 最终得到的结果与后序遍历的结果正好相反
    let arr = []
    let stack = [root]
    if(!root) return []
    while(stack.length){
        let node = stack.pop()
        arr.push(node.val)
        node.left&&stack.push(node.left)
        node.right&&stack.push(node.right)
    }
    return arr.reverse()
};

102.二叉树的层序遍历

方法一：递归

var levelOrder = function(root) {
    //递归实现
    let arr = []
    const level = (root,i) =>{
        if(!root) return
        level(root.left,i+1)
        // arr[i] = arr[i]?arr[i].push(root.val):[root.val]
        arr[i]?arr[i].push(root.val):arr[i] = [root.val]
        level(root.right,i+1)
    }
    level(root,0)
    return arr
};

方法二：迭代 使用队列

/**
 * @param {TreeNode} root
 * @return {number[][]}
 层序遍历相当于广度优先遍历 需要借助一个队列   
 */
var levelOrder = function(root) {
    //使用队列
    let arr = []
    let queue = [root]
    let i = 0
    if(!root) return []
    while(queue.length){
        //记录当前队列的长度
        let len = queue.length
        //用来存储当前层结点
        let tempArr = []
        for(let i=0;i<len;i++){
            //出队
            let node = queue.shift()
            tempArr.push(node.val)
            node.left&&queue.push(node.left)
            node.right&&queue.push(node.right)
        }
        arr.push(tempArr)
    }
    return arr
};

617.合并二叉树

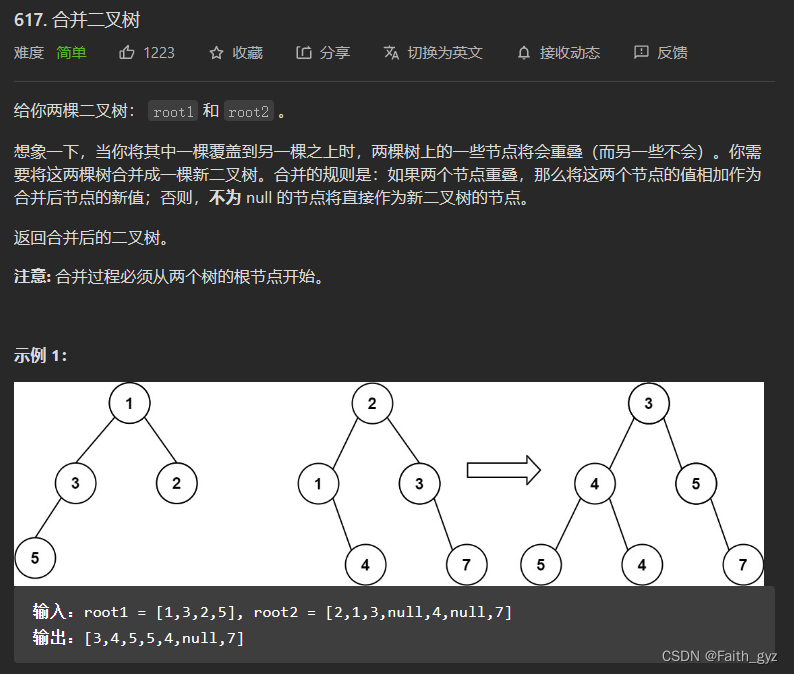
方法一：递归

当看不懂递归的时候，参考二叉树的递归执行过程

var mergeTrees = function(root1, root2) {
    //使用递归
    const merge = (root1,root2) =>{
        //递归跳出的条件
        if(root1==null){
            return root2
        }
        if(root2==null){
            return root1
        }
        //创建新的结点
        //递归的过程是 ①创建newNode 调用27行的递归 一直到左侧递归的最深层次，返回一个root 返回上一个递归函数（这个递归函数会继续执行28行递归，直到其right结点全都为空）  真的很复杂
        let newNode = new TreeNode(root1.val+root2.val)
        newNode.left = merge(root1.left,root2.left)
        newNode.right = merge(root1.right,root2.right)
        return newNode
    }
    return merge(root1,root2)
};

//这里直接修改root1
var mergeTrees = function(root1, root2) {
   //重新去写一遍
   const merge = (root1,root2) =>{
       //递归的出口
       if(root1==null){
           return root2
       }
       if(root2==null){
           return root1
       }
       //这里用的是前序遍历
       root1.val += root2.val
       root1.left = merge(root1.left,root2.left)
       root1.right = merge(root1.right,root2.right)
       //返回上一层递归
       return root1
   }
   return merge(root1,root2)
};

方法二：使用队列

var mergeTrees = function(root1, root2) {
   //root1 root2进入同一个栈
   if(root1==null) return root2
   if(root2==null) return root1
   let queue = []
   queue.push(root1)
   queue.push(root2)
   while(queue.length){
       let node1 = queue.shift()
       let node2 = queue.shift()
       node1.val += node2.val
       if(node1.left!==null&&node2.left!==null){
           queue.push(node1.left)
           queue.push(node2.left)
       }
       if(node1.left==null&&node2.left!==null){
           node1.left = node2.left
       }
       if(node1.right&&node2.right){
           queue.push(node1.right)
           queue.push(node2.right)
       }
       if(node1.right==null&&node2.right!==null){
           node1.right = node2.right
       }
   }
   return root1
};

226.翻转二叉树

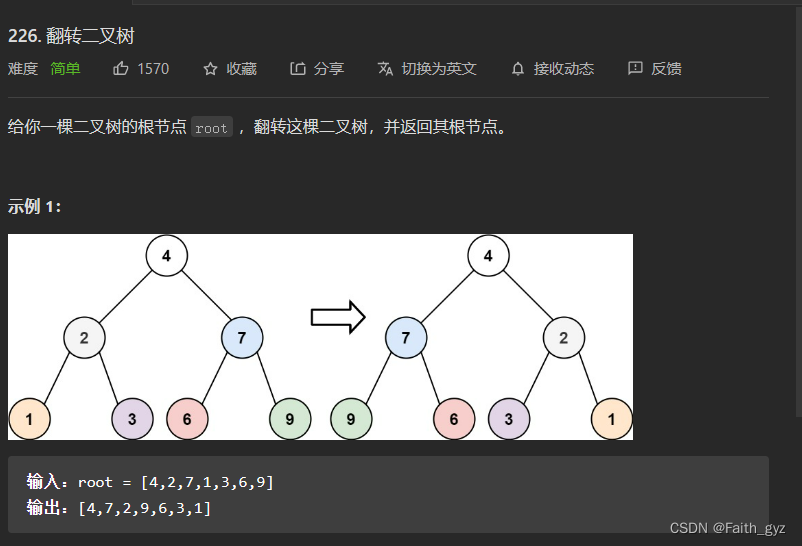
方法一：递归

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 整个树的交换过程中，会把真个node结点下面的所有的结点都会交换过来
 */
var invertTree = function(root) {
    //递归实现
    if(!root) return root
    const invert = root =>{
        //递归出去的条件
        if(root==null) return null
        //递归
        let temp = invert(root.left)
        root.left = invert(root.right)
        root.right = temp
        return root
    }
    return invert(root)
};

方法二：前序遍历过程中实现交换

/**
 * @param {TreeNode} root
 * @return {TreeNode}
 整个树的交换过程中，会把真个node结点下面的所有的结点都会交换过来
 */
var invertTree = function(root) {
    //前序遍历的过程中实现翻转
    if(root==null) return root
    if(root.left==null&&root.right==null) return root
    let stack = [root]
    while(stack.length){
        //出栈
        let node = stack.pop()
        //进行交换  如果node.left不存在 那么node.left=null
        let temp = node.left
        node.left = node.right
        node.right = temp
        //入栈
        node.left&&stack.push(node.left)
        node.right&&stack.push(node.right)
    }
    return root
};

方法三：层序遍历过程中实现交换

var invertTree = function(root) {
    //层序遍历过程中实现
    if(root==null) return root
    if(root.left==null&&root.right==null) return root
    let queue = [root]
    while(queue.length){
        //出队
        let node = queue.shift()
        //进行交换
        let temp = node.left
        node.left = node.right
        node.right = temp
        //入队
        node.left&&queue.push(node.left)
        node.right&&queue.push(node.right)

    }
    return root
};

101.对称二叉树

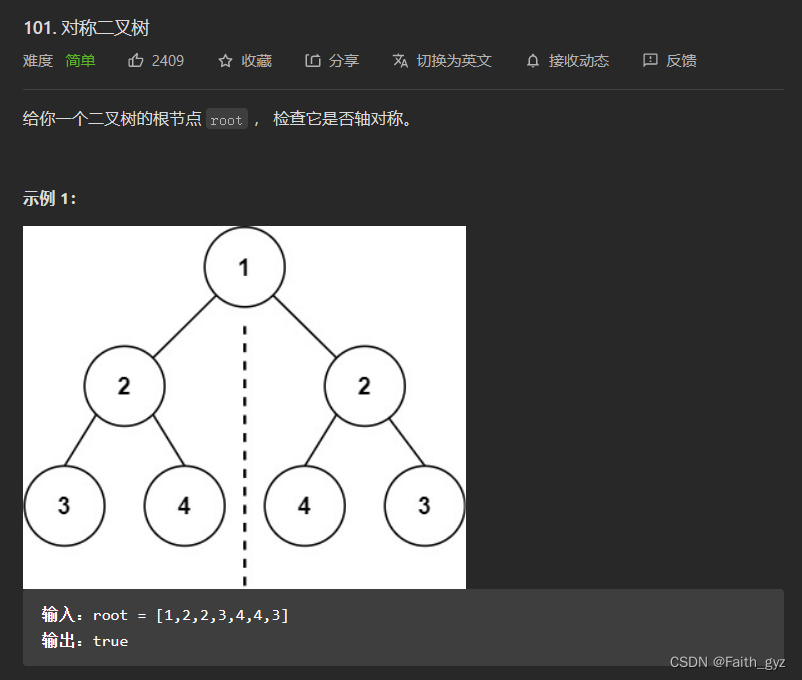
方法一:递归

var isSymmetric = function(root) {
    //同时进去两个节点 left and right
    const compare = (root1,root2) =>{
        if(root1==null&&root2==null){
            return true
        }else if(root1==null&&root2!==null || root1!==null&&root2==null){
            return false
        }else if(root1.val!==root2.val){
            return false
        }
        //递归持续下去的条件  左右都得满足
        let outside = compare(root1.left,root2.right)
        let inside  = compare(root1.right,root2.left)
        return outside&&inside
    }
    return compare(root.left,root.right)
};

方法二：使用队列

var isSymmetric = function(root) {
    //队列实现
    if(root==null){
        return true
    }else if(root.left==null&&root.right==null){
        return true
    }else if(root.left!==null&&root.right==null || root.left==null&&root.right!==null){
        return false
    }
    
    let queue = []
    queue.push(root.left)
    queue.push(root.right)
    while(queue.length){
        let node1 = queue.shift()
        let node2 = queue.shift()
        if(node1.val!==node2.val){
            return false
        }
        if(node1.left==null&&node2.right!==null || node1.left!==null&&node2.right==null){
            return false
        }
        if(node1.right==null&&node2.left!==null || node1.right!==null&&node2.left==null){
            return false
        }
        node1.left&&queue.push(node1.left)
        node2.right&&queue.push(node2.right)
        node1.right&&queue.push(node1.right)
        node2.left&&queue.push(node2.left)
    }
    return true
};


//或者
var isSymmetric = function(root) {
    //队列实现
    if(root==null){
        return true
    }
    //入队   先去入队 出队的时候再去判断是否为空
    let queue = []
    queue.push(root.left)
    queue.push(root.right)
    //如果root.left right都是空的话  就不会有下面的while循环 直接跳出去了
    while(queue.length){
        let leftNode = queue.shift()
        let rightNode = queue.shift()
        if(leftNode==null&&rightNode==null){
            //进入下一层循环
            continue
        }
        if(leftNode==null || rightNode==null || leftNode.val!==rightNode.val){
            return false
        }
        queue.push(leftNode.left)
        queue.push(rightNode.right)
        queue.push(leftNode.right)
        queue.push(rightNode.left)
    }
    return true
};

方法三：使用栈实现

var isSymmetric = function(root) {
    //栈实现
    let stack = []
    if(root==null){
        return true
    }
    stack.push(root.left)
    stack.push(root.right)
    while(stack.length){
        let leftNode = stack.pop()
        let rightNode = stack.pop()
        if(leftNode==null&&rightNode==null){
            //进入下一层循环
            continue
        }
        if(leftNode==null || rightNode==null || leftNode.val!==rightNode.val){
            return false
        }
        stack.push(leftNode.left)
        stack.push(rightNode.right)
        stack.push(leftNode.right)
        stack.push(rightNode.left)
    }
    return true
};

543.二叉树的直径

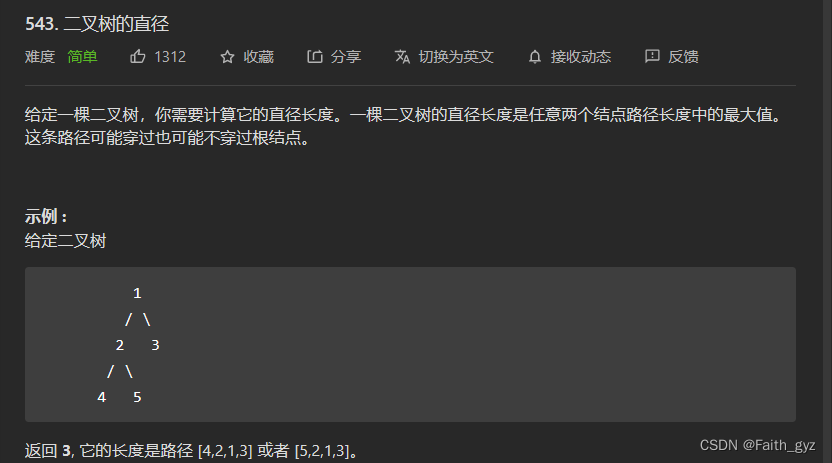
var diameterOfBinaryTree = function(root) {
  //二叉树的直径==根节点左右两侧高度之和的最大值
  let res = 0 //用来记录递归过程中遇到的和的最大值
  if(!root) return 0
  const diameter = root =>{
      if(root==null) return 0
      let leftHeight = diameter(root.left)
      let rightHeight = diameter(root.right)
      res = Math.max(res,(leftHeight+rightHeight))
      return Math.max(leftHeight,rightHeight)+1   //这是返回给上一层递归的结果值
  }
  diameter(root)
    return res
};

104.二叉树的最大深度

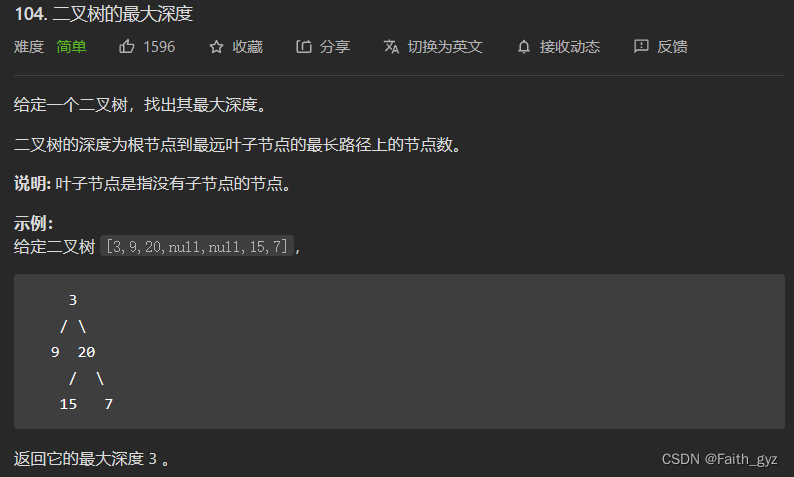
方法一：层序遍历之后，计算res的length

var maxDepth = function(root) {
   //方法一：层序遍历之后，将其放入到数组中，然后判断数组的长度
   let res = []
   if(root==null) return 0
   const level = (root,i) =>{
       if(root==null){
           return
       }
       //中序遍历的过程中进行压栈处理
       level(root.left,i+1)
       res[i]?res[i].push(root.val):res[i]=[root.val]
       level(root.right,i+1)
   }
   level(root,0)
   return res.length
};

//层序遍历过程中 不进行压栈处理
var maxDepth = function(root) {
   //层序遍历的过程中动态记录最大的深度
   let max = 0
   if(root==null) return 0
   const level = (root,i)=>{
       if(root==null){
           return
       }
       level(root.left,i+1)
       max = Math.max(max,i)
       level(root.right,i+1)
   }
   level(root,0)
   return max+1
};

方法二：同二叉树最大直径的求解过程

var maxDepth = function(root) {
   //利用二叉树最大直径的处理过程中 类似
   const maxit = root =>{
       if(root==null) return 0
       let leftHeight = maxit(root.left)
       let rightHeight = maxit(root.right)
       return Math.max(leftHeight,rightHeight) +1
   }
   return maxit(root) 
};

方法三:使用队列

var maxDepth = function(root) {
   //使用队列
   if(root==null) return 0
   let queue = [root]
   let arr = []
   while(queue.length){
       let len = queue.length
       let temp = []
       for(let i=0;i<len;i++){
           let node = queue.shift()
           temp.push(node.val)    
           node.left&&queue.push(node.left)
           node.right&&queue.push(node.right)
       }
       arr.push(temp)
   }
   return arr.length
};



//优化
var maxDepth = function(root) {
   //使用队列
   if(root==null) return 0
   let queue = [root]
   let max = 0
   while(queue.length){
       let len = queue.length
       for(let i=0;i<len;i++){
           let node = queue.shift()    
           node.left&&queue.push(node.left)
           node.right&&queue.push(node.right)

       }
       max++
   }
   return max
};

105.从前序与中序遍历序列中构造二叉树

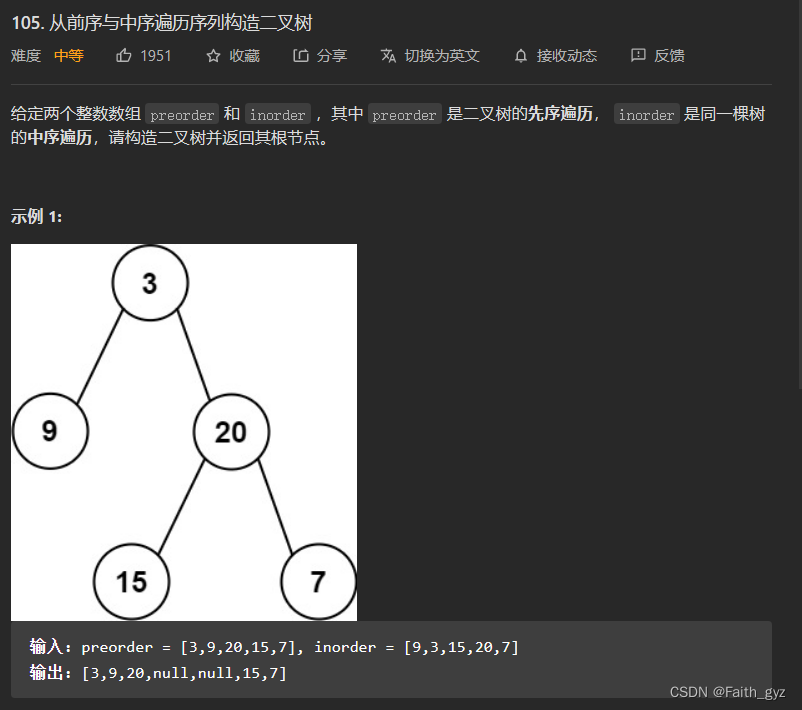
方法一：递归过程中不断进行截取数组

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 给定二叉树的前序遍历和中序遍历 如何构造二叉树 没有一点思路
 */
var buildTree = function(preorder, inorder) {
    //暴力解法
    //思路：首先，preorder中的第一个结点是root结点 然后根据这个root结点在inorder中进行划分，分为前后段 
    //根据前后两段的长度大小 将inorder进行截取，根据长度大小找出root的左子树的长度和右子树的长度
    //我最开始用的是preorder==null进行判断，这样是错误的，preorder是一个数组 你知道吗
    //我发现判断preorder或者是inorder都是可以的
    if(preorder.length==0) return null
    //创建根节点
    let root = new TreeNode(preorder[0])
    //根据根节点找出root这个值所在的索引
    let mid = inorder.indexOf(preorder[0])
    //递归开始 
    //前序遍历的结果 除了第一个是根节点 然后是他的左子树 完了之后才是右子树 只要保证左子树的个数一致那么在前序遍历中进行截取就可以了
    root.left = buildTree(preorder.slice(1,mid+1),inorder.slice(0,mid))
    root.right = buildTree(preorder.slice(mid+1),inorder.slice(mid+1))
    return root
};

只记录索引，不进行截取

var buildTree = function(preorder, inorder) {
    //不需要每次都进行截取数组，这样会造成浪费 只要记录索引即可
    const build = (pre_start,pre_end,in_start,in_end) =>{
        //如果二者相等 意思是只剩下一个节点了
        if(pre_start > pre_end){
            return null
        }
        //取根节点
        let root = new TreeNode(preorder[pre_start])
        //找到mid结点
        let mid = inorder.indexOf(preorder[pre_start])
        //记录左子树的长度   因为左子树是不包括mid的，所以这里不用加一
        let len = mid - in_start
        //开始递归
        root.left = build(pre_start+1,pre_start+len,in_start,mid-1)
        root.right = build(pre_start+len+1,pre_end,mid+1,in_end)
        return root
    }
    return build(0,preorder.length-1,0,inorder.length-1)
};

加入map数组来记录mid的信息

var buildTree = function(preorder, inorder) {
    //由于每次找到mid需要使用indexof进行遍历，这需要花费较大的时间 可以使用map对象进行保存
    let map = new Map()
    for(let i=0;i<inorder.length;i++){
        map.set(inorder[i],i)
    }
    //不需要每次都进行截取数组，这样会造成浪费 只要记录索引即可
    const build = (pre_start,pre_end,in_start,in_end) =>{
        //如果二者相等 意思是只剩下一个节点了
        if(pre_start > pre_end){
            return null
        }
        //取根节点
        let root = new TreeNode(preorder[pre_start])
        //找到mid结点
        // let mid = inorder.indexOf(preorder[pre_start])
        let mid = map.get(preorder[pre_start])
        //记录左子树的长度   因为左子树是不包括mid的，所以这里不用加一
        let len = mid - in_start
        //开始递归
        root.left = build(pre_start+1,pre_start+len,in_start,mid-1)
        root.right = build(pre_start+len+1,pre_end,mid+1,in_end)
        return root
    }
    return build(0,preorder.length-1,0,inorder.length-1)
};

106.后序和中序遍历序列创建二叉树

var buildTree = function(inorder, postorder) {
    //递归中进行截取
    if(inorder.length==0){
        return null
    }
    //这里也可以将获取后序遍历序列的最后一个结点 即当前序列的root结点
    // let rootVal = postorder.pop()
    let rootVal= postorder[postorder.length-1] 
    let root = new TreeNode(rootVal)    
    //找到中间节点 中序序列中mid左侧的都是左子树 右侧的是右子树 故此时左子树的长度是mid
    //后序遍历序列中 顺序是 左右根
    let mid = inorder.indexOf(rootVal)
    root.left = buildTree(inorder.slice(0,mid),postorder.slice(0,mid))
    root.right = buildTree(inorder.slice(mid+1),postorder.slice(mid,postorder.length-1))
    // root.right = buildTree(inorder.slice(mid+1),postorder.slice(mid))
    return root
};

96.不同的二叉搜索树

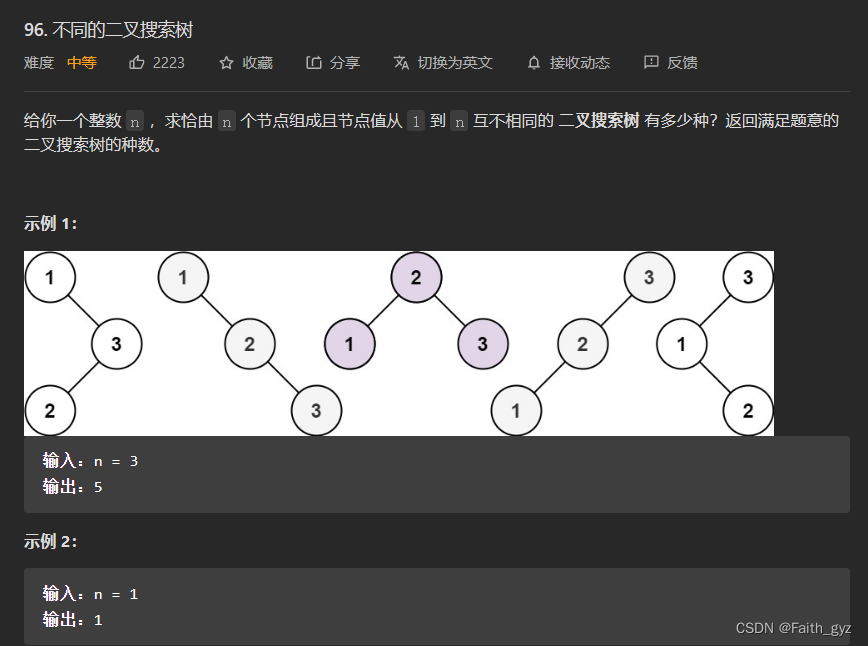
方法一：动态规划

/**
 * @param {number} n
 * @return {number}
 二叉搜索树：左子树的节点值总是小于根节点的值  根节点的值总是小于右子树的节点值

 总的次数==根节点 左子树二叉搜索树的个数*右子树二叉搜索树的个数
 */
var numTrees = function(n) {
    //方法一：迭代法
    //创建一个数组来保存 n个结点的二叉搜索树的数量
    let arr = new Array(n+1).fill(0)
    arr[0]=1
    arr[1]=1
    //当前二叉树总共有多少个结点
    for(let i=2;i<=n;i++){
        //必须得保证有一个结点是根节点 其他的结点分成左右子树
        for(let j=0;j<=i-1;j++){
            arr[i]+=arr[j]*arr[i-j-1]
        }
    }
    return arr[n]
};

方法二：递归

var numTrees = function(n) {
    //使用递归
    const induce = n =>{
        //递归出去的条件
        if(n==0||n==1){
            return 1
        }
        //每轮递归这里的count都是0
        let count = 0
        //这里的i是一侧子树可以有的结点的个数
        for(let i=0;i<=n-1;i++){
            count+=induce(i)*induce(n-i-1)
        }
        //这里是不对的
        // for(let i=2;i<=n;i++){
        //     for(let j=0;j<=i-1;j++){
        //         count+=induce(j)*induce(i-j-1)
        //     }
        // }
        return count
    }
    return induce(n)
};

//使用res数组来保存曾经遍历过的 大大的节省时间
var numTrees = function(n) {
    //使用递归
    //使用res来保存曾经遍历过的 这样可以节省时间
    let res = []
    const induce = n =>{
        //递归出去的条件
        if(n==0||n==1){
            return 1
        }
        if(res[n]){
            return res[n]
        }
        //每轮递归这里的count都是0
        let count = 0
        //这里的i是一侧子树可以有的结点的个数
        for(let i=0;i<=n-1;i++){
            count+=induce(i)*induce(n-i-1)
        }
        res[n] = count
        //这里是不对的
        // for(let i=2;i<=n;i++){
        //     for(let j=0;j<=i-1;j++){
        //         count+=induce(j)*induce(i-j-1)
        //     }
        // }
        return count
    }
    return induce(n)

};

538.将二叉搜索树转换成累加树

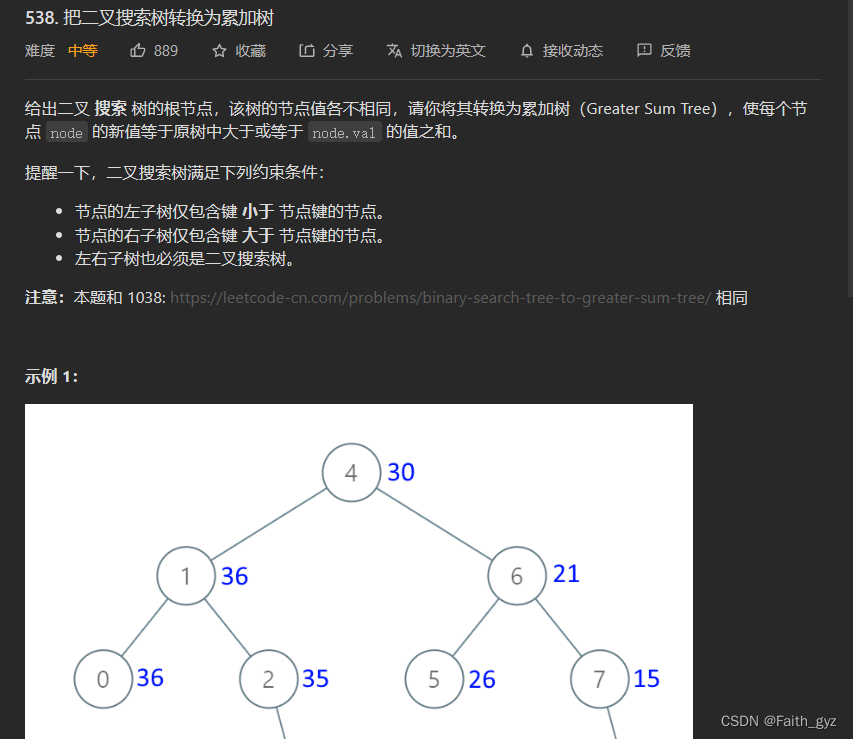
var convertBST = function(root) {
    //前序遍历之后是从小到大   如果是右 根 左 那么结果就是从大到小
    let count = 0
    const convert = root =>{
        if(root==null){
            return
        }
        convert(root.right)
        root.val+=count
        //这样count始终是大于当前节点值的所有的和
        count = root.val
        convert(root.left)
    }
    convert(root)
    return root
};

114.二叉树展开为链表

注意：只能原地进行移动

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {void} Do not return anything, modify root in-place instead.
 */
var flatten = function(root) {
     //题目已经说了 只能原地进行移动 

     //递归跳出的条件
     if(root==null){
         return
     }
     flatten(root.left)
     flatten(root.right)

     //记录当前root结点的左右子树
     let left = root.left
     let right = root.right

     //将左子树移动到原来的右子树的位置
     root.left = null
     root.right = left

     //判断移动之后的右子树是否为空 如果不为空 将root原来的右子树放到当前右子树的末端
     while(root.right){
         //一直往右走 知道为空 然后再将原来的右子树连接到最右端
         root = root.right
     }
     root.right = right
};

236.二叉树的最近的公共祖先

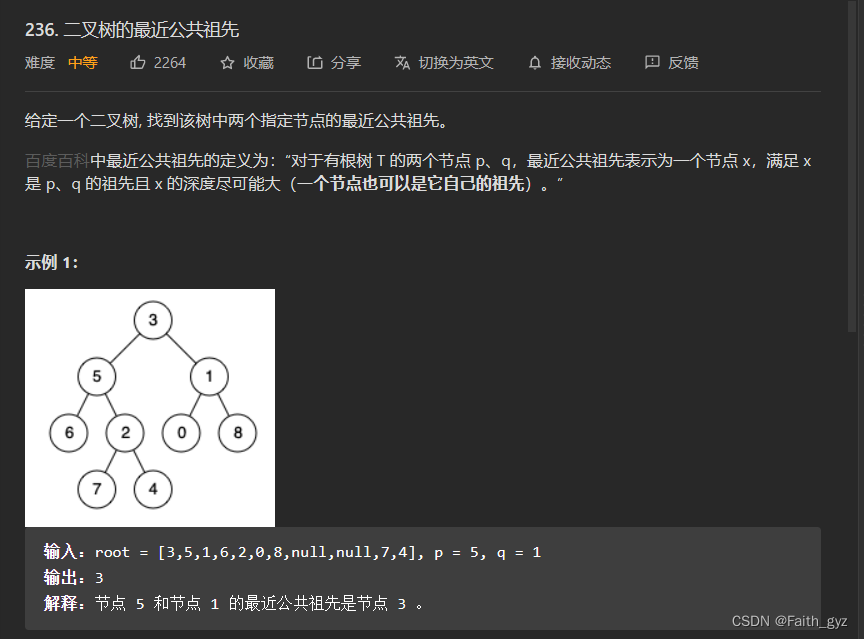
思路：
①如果遍历到p或者q，那么公共的结点只能在当前这个结点之上，直接返回就可以
②如果当前遍历到的节点是null，返回
③如果在遍历过程中没有找到p或者q，那么在他们的左右子树上进行查找
1.left right都不是空 =>p q在root的两侧
2.left 或者right有一个为空 p q在root的同一侧
3.如果都是null 说明p q都不在这个子树中

var lowestCommonAncestor = function(root, p, q) {
    const induce =  (root,p,q)=>{
        //递归跳出的条件   如果找到了p或者q那么直接返回就可 不用再去遍历他的子树了
        if(root==null||root==p||root==q) return root
        //当前节点不是null 也不是p或者q 就往他的左右子树中进行查找
        //往左子树进行查找
        let left = lowestCommonAncestor(root.left,p,q)
        //往右子树进行查找
        let right = lowestCommonAncestor(root.right,p,q)
        //这种情况只能是一边一个 就是p q在root的两侧  里p q最近的是root
        if(left&&right){
            return root
        }else if(left&&!right){
            //p q 都在左子树上
            return left
        }else if(!left&&right){
            return right
        }else{
            return null
        }
    }
    return induce(root,p,q)
};