当前位置：首页 > article >正文

学习Transformer前言（Self Attention Multi head self attention）

article 2024/9/22 13:40:58

一、前言

一直在做项目，也比较懒没有挤出时间去学习新的东西，感觉停滞很久了，好长一段时间都没有新的知识输入，早就需要就去学习transformer了，因此先来学习注意力机制，本文为个人的一个笔记总结。主要是基于李宏毅老师的一个课程视频笔记，论文原文，加上B站UP主的霹雳吧啦Wz的视频。

二、理论

2.1模型的输入类别

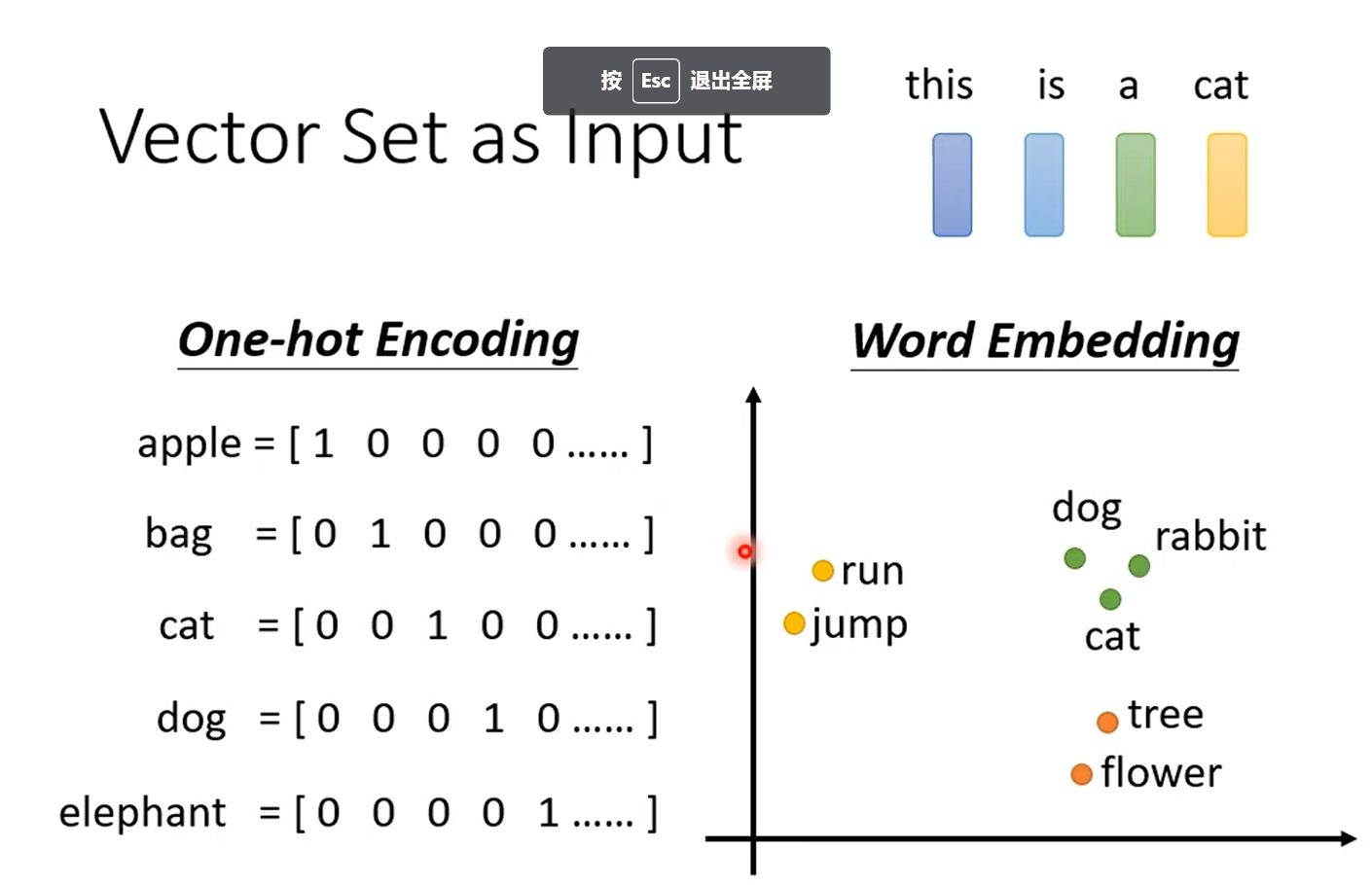
self-attention和CNN不同，这是另外一种网络结构，与CNN不同，网络输入不再是一个向量，而是一个向量序列，而且输入的向量序列长度是不定的。举例，在文字处理时，我们需要输入一个句子判断它的每一个单词的词性，如果我们输入this is a cat, 可以使用onehot向量来表示每一个单词，可以把这个onehot向量维度设为超大的一个向量，这样onehot编码就能表示所有的向量了，但是这样编码是会带来很大的问题，因为这样编码相当于假设所有的词汇之间是没有任何关系的，这显然是不合理的，因为dog和cat和明显都是动物，它们之间是有关联的。

为了解决上面的问题，研究者提出word embedding的方法，这种编码方式就将单词之间的联系考虑了进去。

其他可能需要多个向量作为向量序列作为输入的情况，例如：语音的输入编码，分子结构，图网络等。

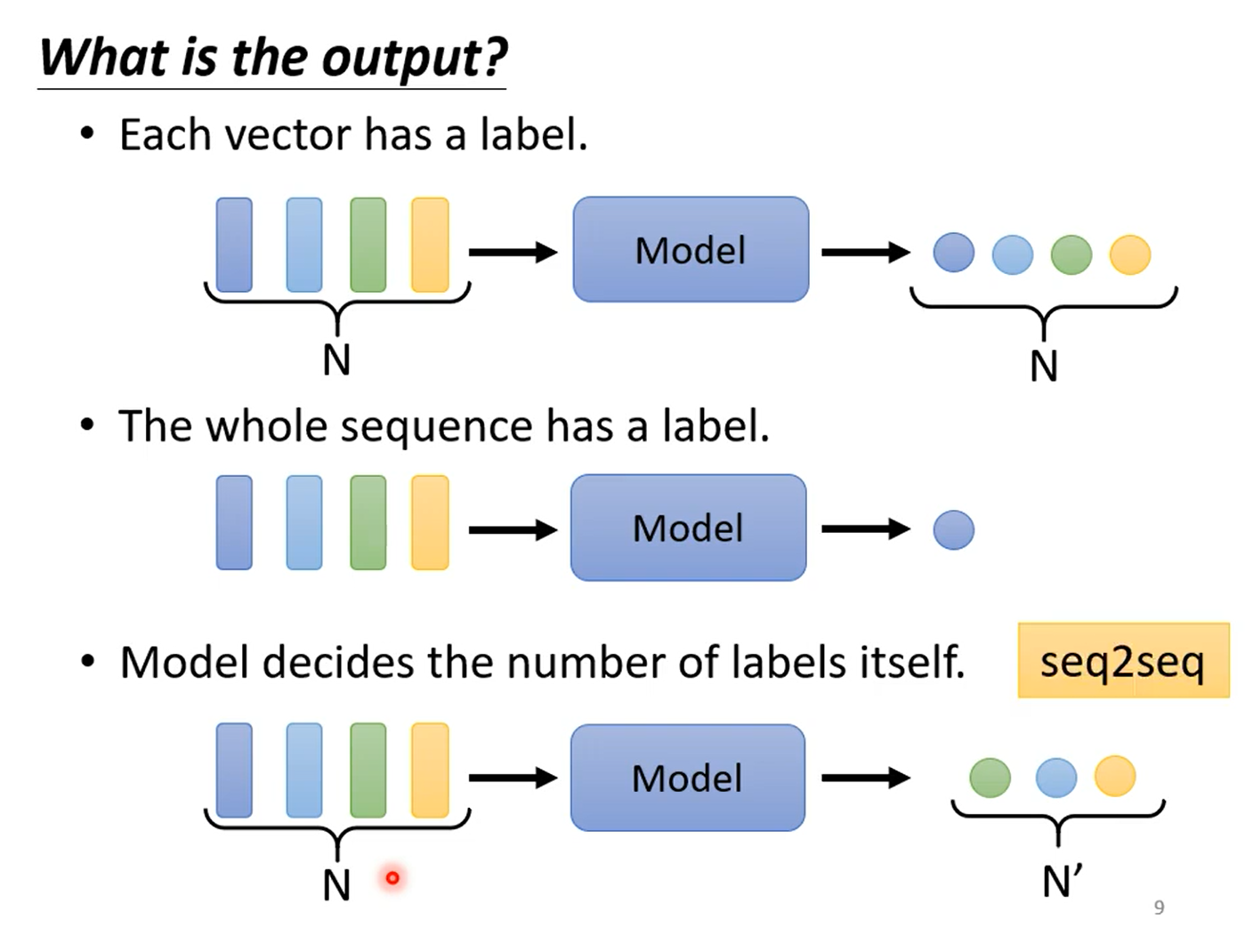
2.2模型的输出类别

有三种情况，第一种每一个向量都有一个对应一个输出，输入和输出数量一样多，也称为sequence labeling,第二种整个输入向量只有一个输出，最后一种就是输出个数是不定的。

2.3如何更好的考虑到模型输入？

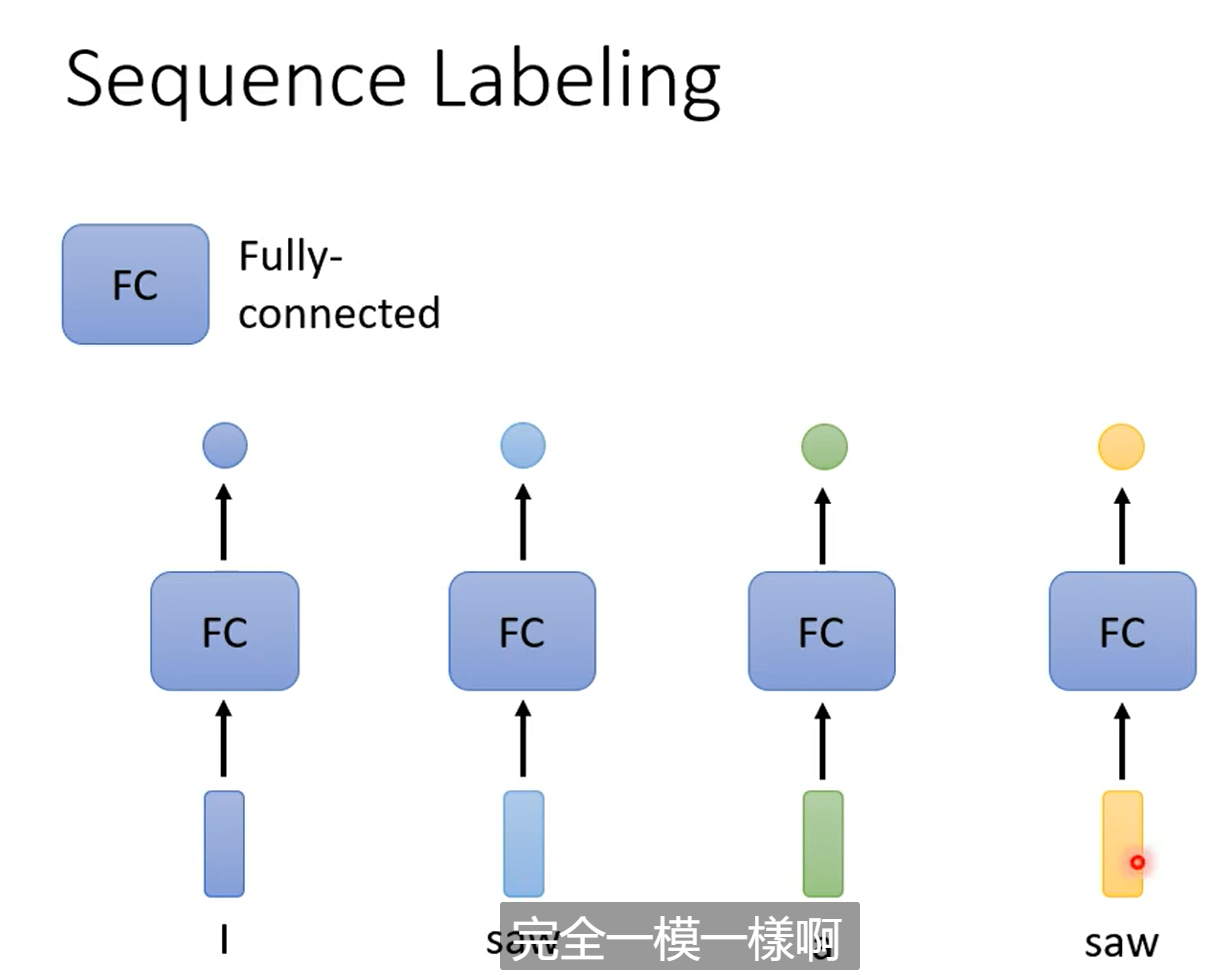
本文基于第一种输出，例如假如我们还是按照以前的做法来进行输出，每一个向量分别输入到全连接层得到对应的结果。看似也能解决问题，但是这其实会存在一些问题，例如如果我们是在做一个词性判断的任务，输入一个句子， I saw a saw，很显然这两个位置的词的词性显然不相同，如果还是采用上面的方式来输入网络，理论上两个saw得到的结果是一样的，因此直接分别输入全连接层得到结果是不合理的，如何改进？很容易就想到我们应该考虑到上下文的关系。也就是在输入每一个向量时候，考虑到其他的向量，这样就包含了上下文的关系。

那么如何考虑上下文的关系？

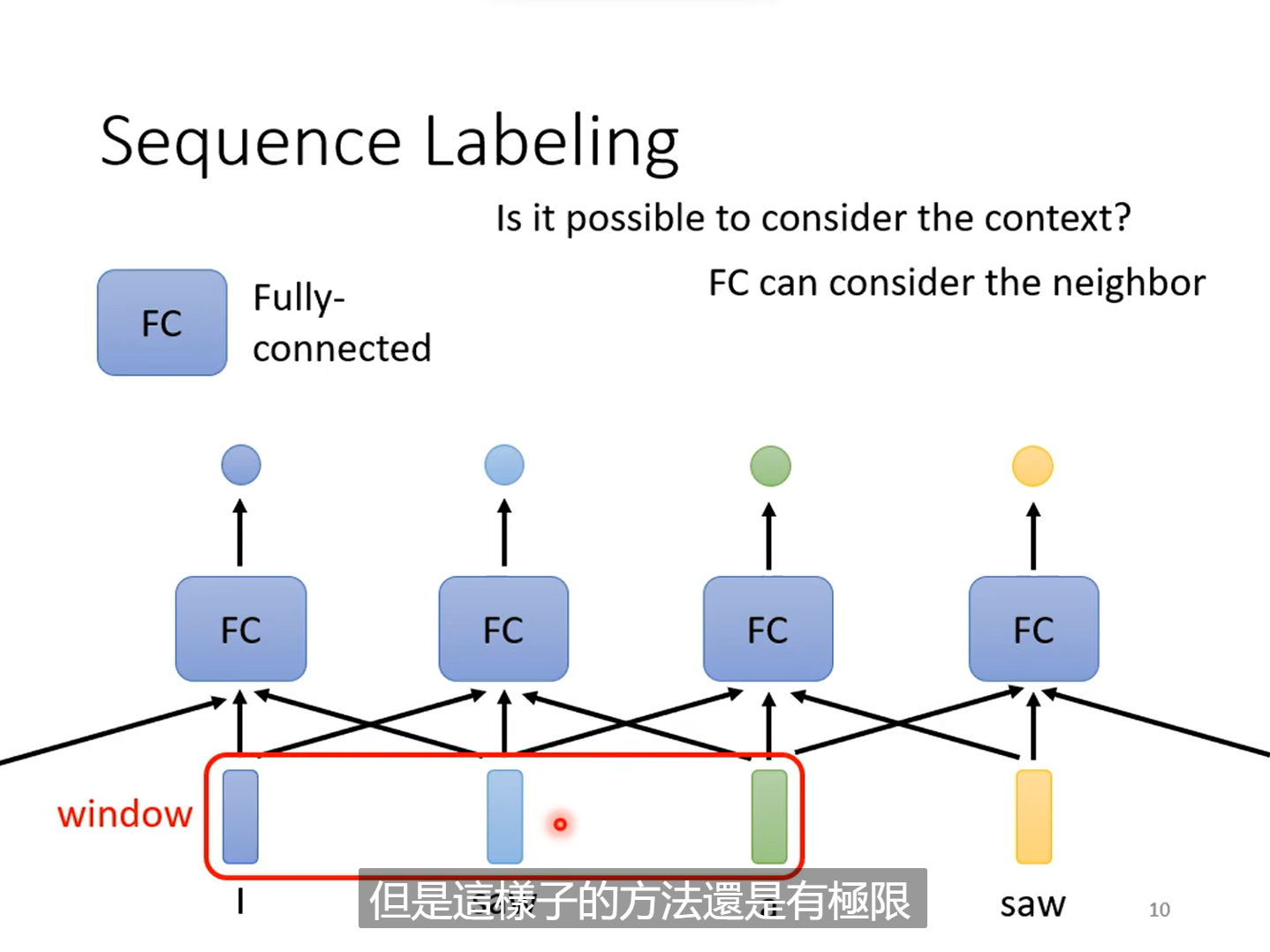
有一种做法就是考虑前后相邻的一个窗口的信息，但是这也存在问题，如何设置这个窗口的长度，有人可能会想提出直接设置窗口长度为最大的向量序列的长度，这会导致全连接层的参数巨大，而且还需要我们去统计向量序列的最长长度。因此这不是很好的方法，因此我们引入的了self-attention

2.4.self-attention的提出

在这里我们引入了self-attention的模块来处理每一个向量，每一个经过self-attention模块的向量都包含了整个向量序列的信息。而且self-attation和卷积一样可以重复使用，可以在经过self-attention处理再继续添加self-attention模块。事实上，虽然self-attention在很多paper已经提出，但提到self-attention往往想到的是transformer,而transformer第一次提出是在Attention is all you need这篇paper。

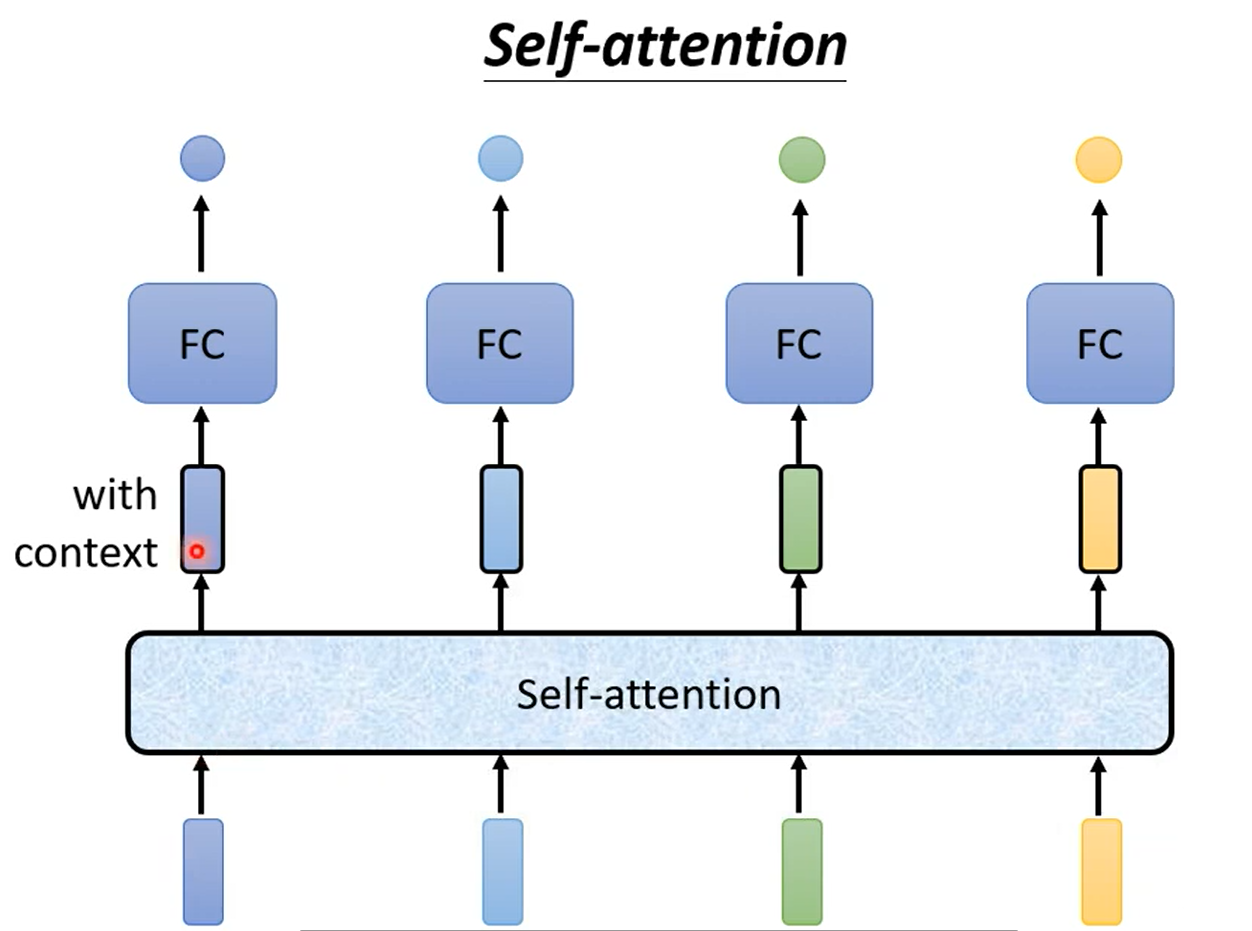
2.5.self-attention模块

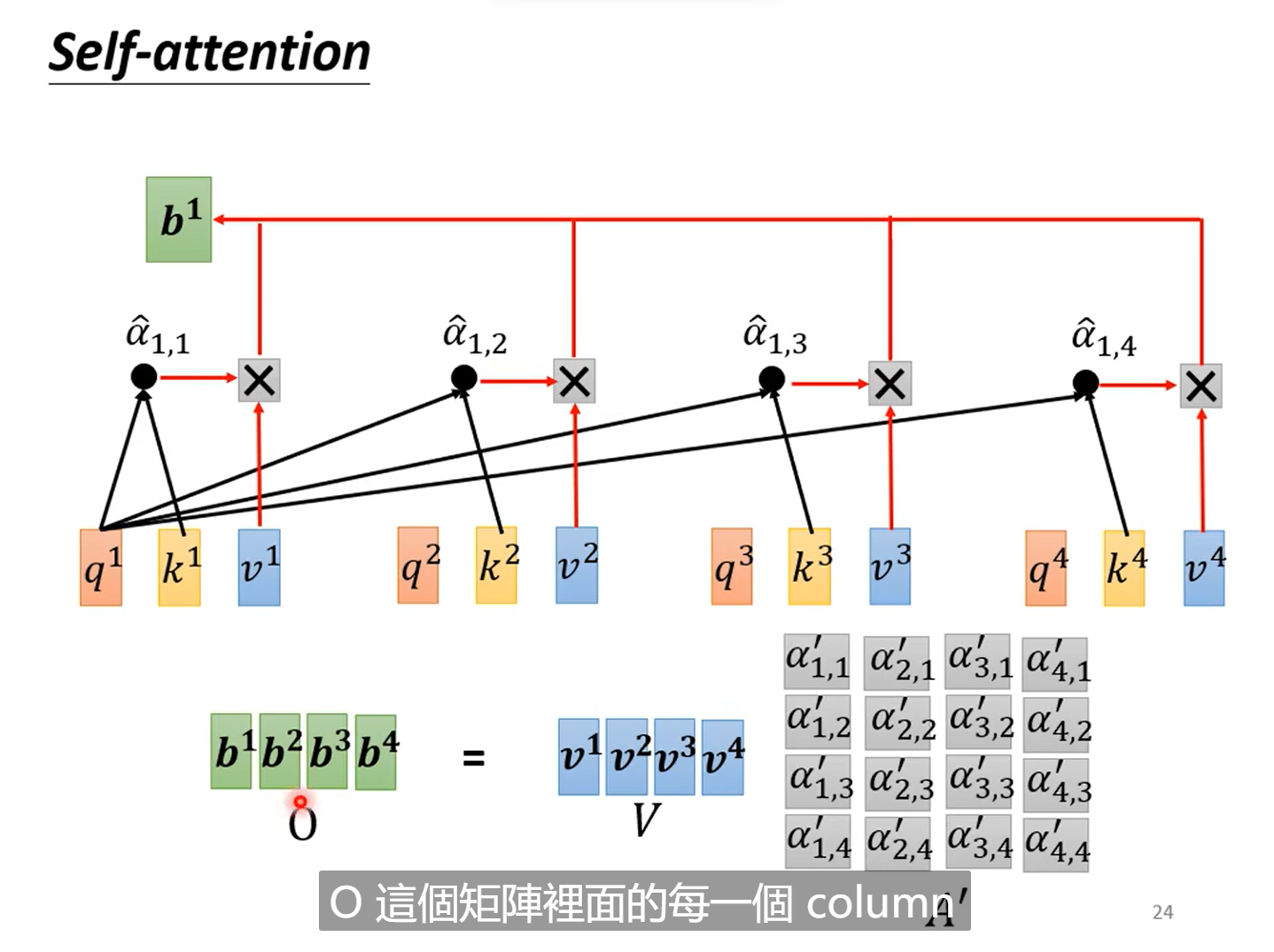
具体来看经过self-attention处理的向量都会考虑到之前输入的整个向量序列的信息。举例来看也就是b1是由a1, a2, a3,a4经过某种操作得到的。

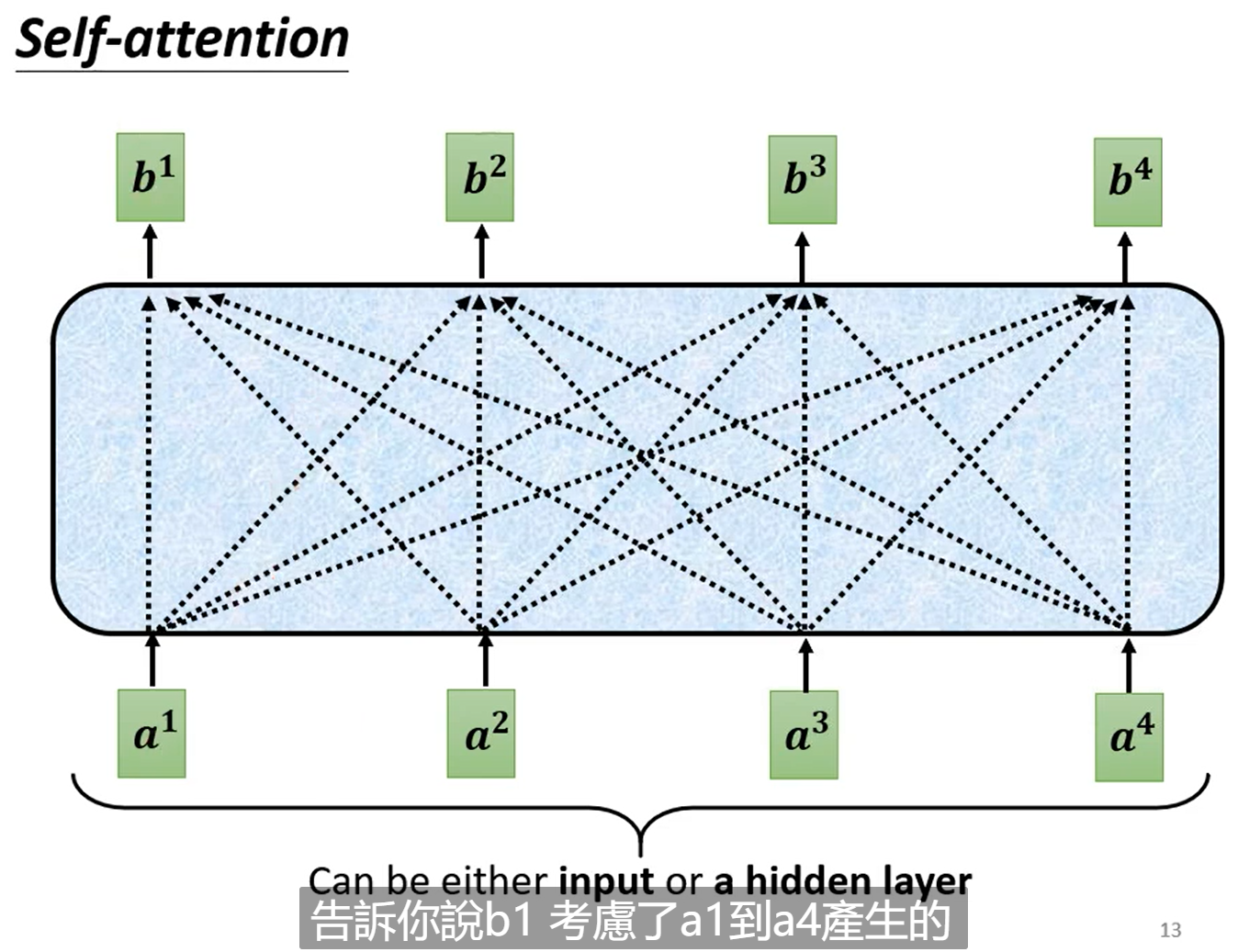
那么这种操作是什么？

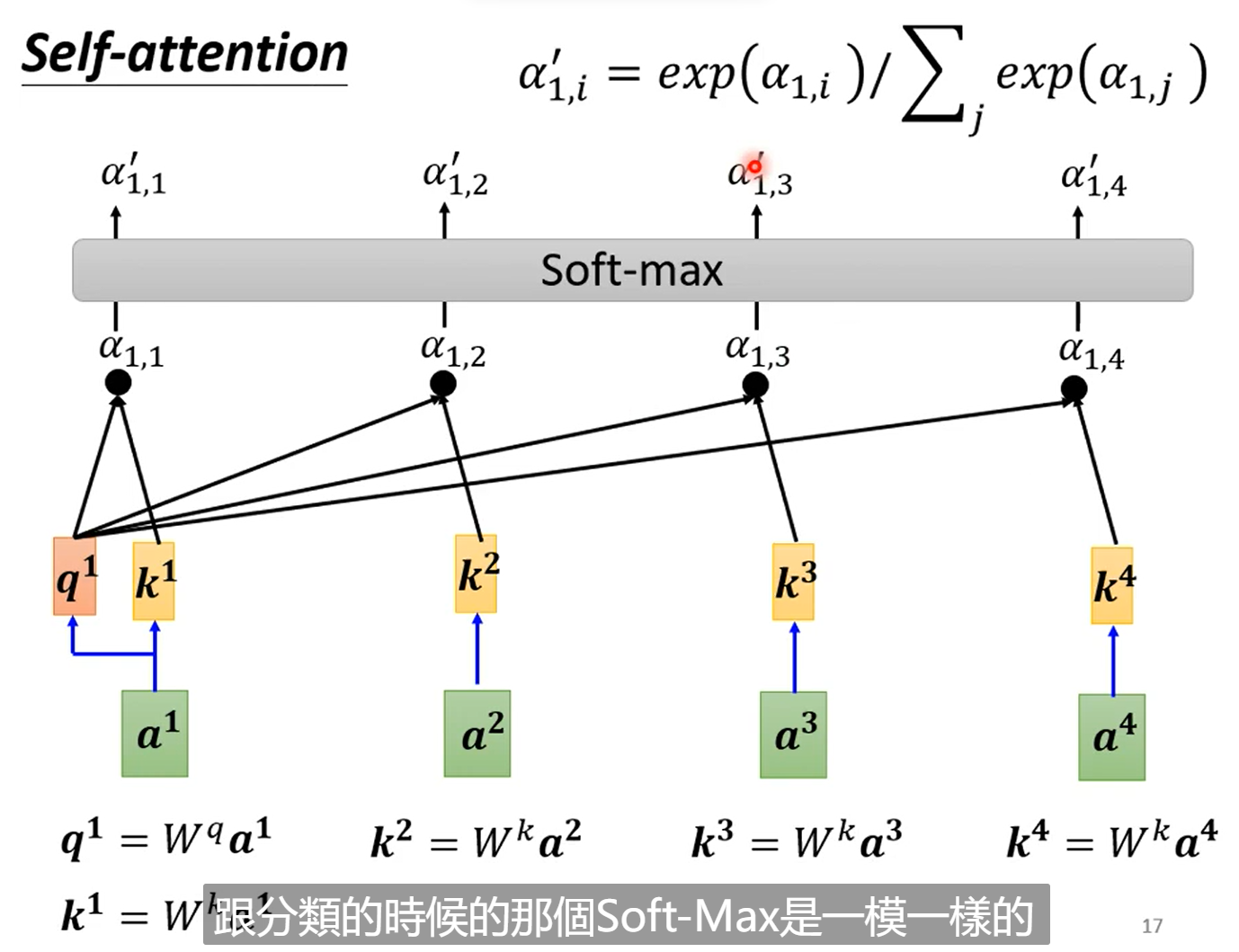
有很多种操作，本文主要是dot-product，前面提到我们需要考虑到整个向量序列的信息，也就是需要知道每两个向量之间的联系，我们可以用α来衡量这两个向量之间的关系。因此dot-product就是输入两个需要计算关系的向量，得到他们的关系。

那么如何操作？

在dot-product中，我们对于输入的两个向量分别乘以𝑊𝑞和𝑊𝑘分别得到q和k，再将q和k做点积得到α（原论文会除以根号d，d为向量的长度，除以根号d的原因主要是为了防止点乘后数值过大，导致softmax处理后梯度很小）

则在整个向量序列计算时就会有如下表：

1	2

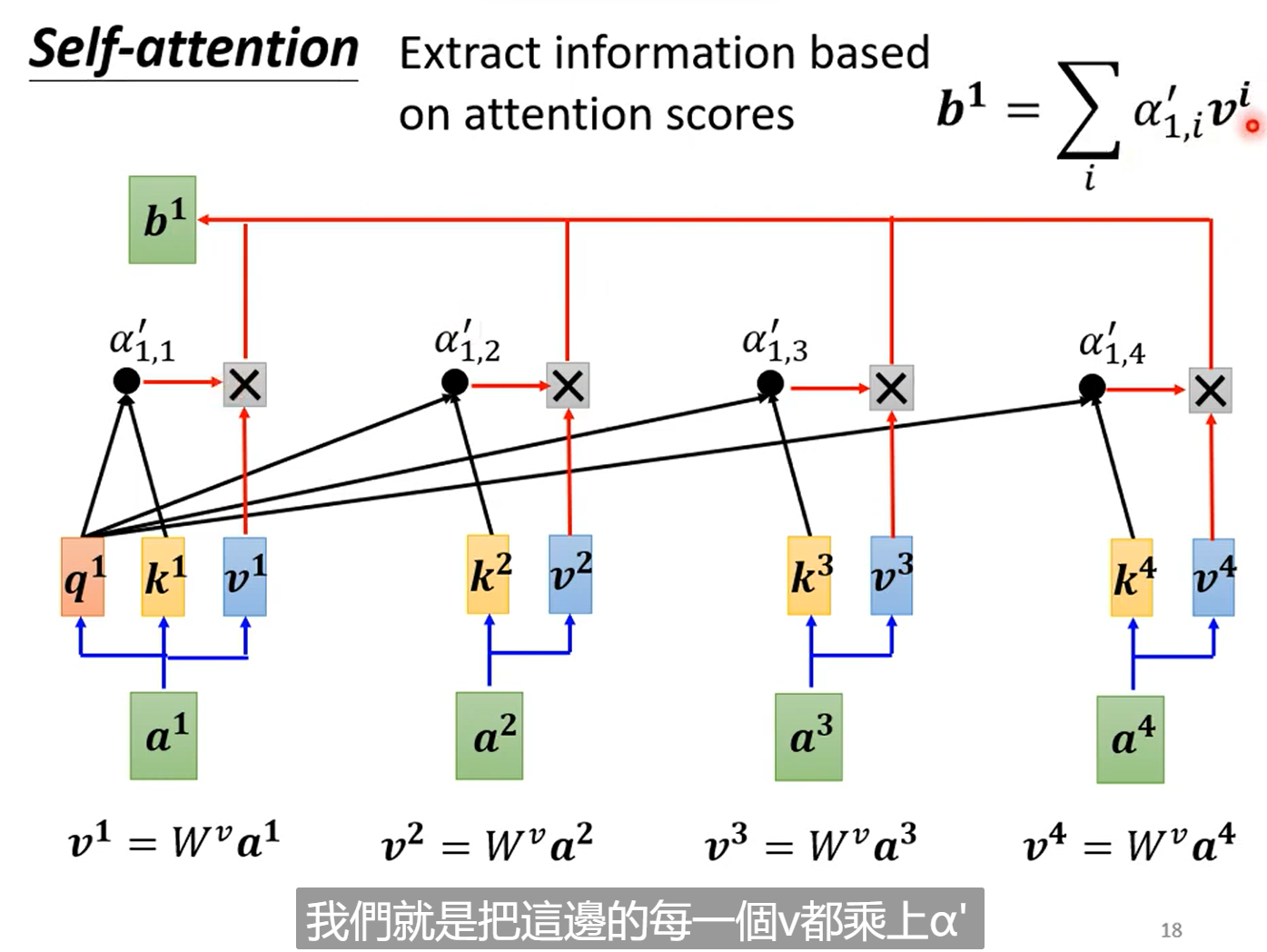
分析：其实可以看到对于一整个self-attention的计算中b1的计算，我们需要先分别计算a1, a2, a3, a4与a1的attention scores也即α，然后经过softmax处理来归一化（softmax处理不是必须的，也可以使用其他的方法），然后我们在分别得到v1, v4,这样最终得到的b1相当于将各个部分乘以权重得到的值。

以上为理论的做法，只计算了单独一个b1,下面主要考虑加入矩阵的思想来得到所有的经过self-attention的值

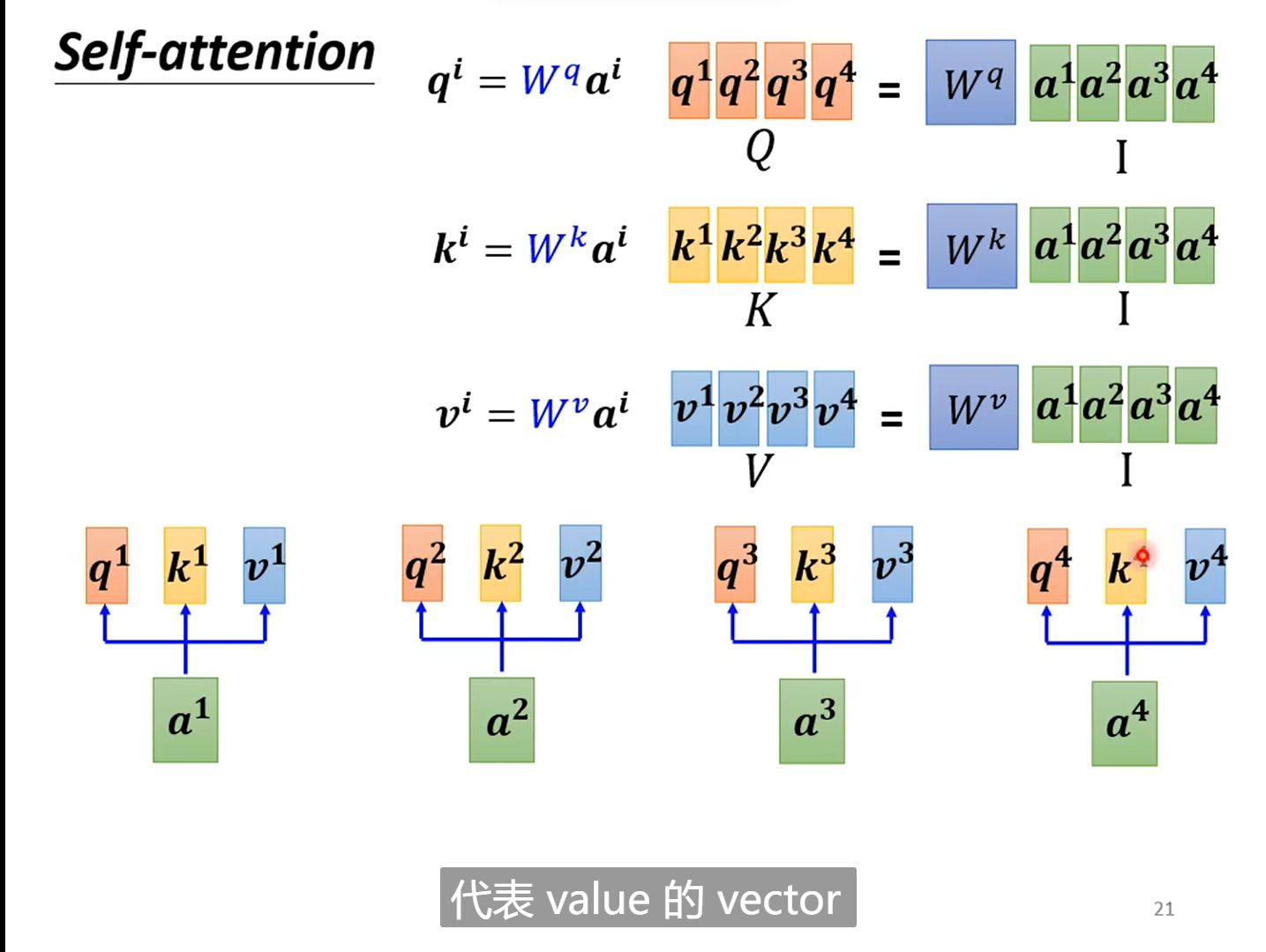
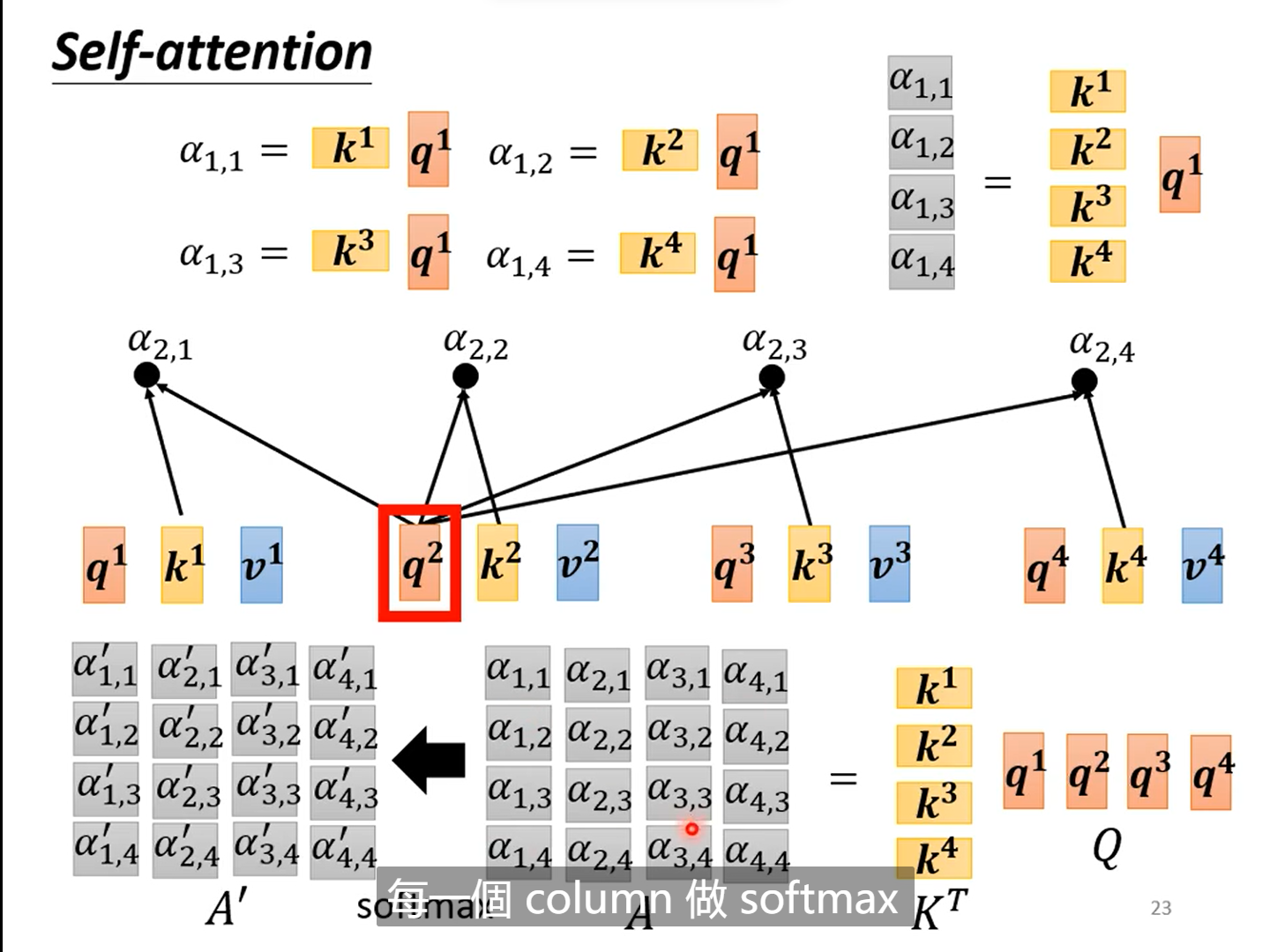
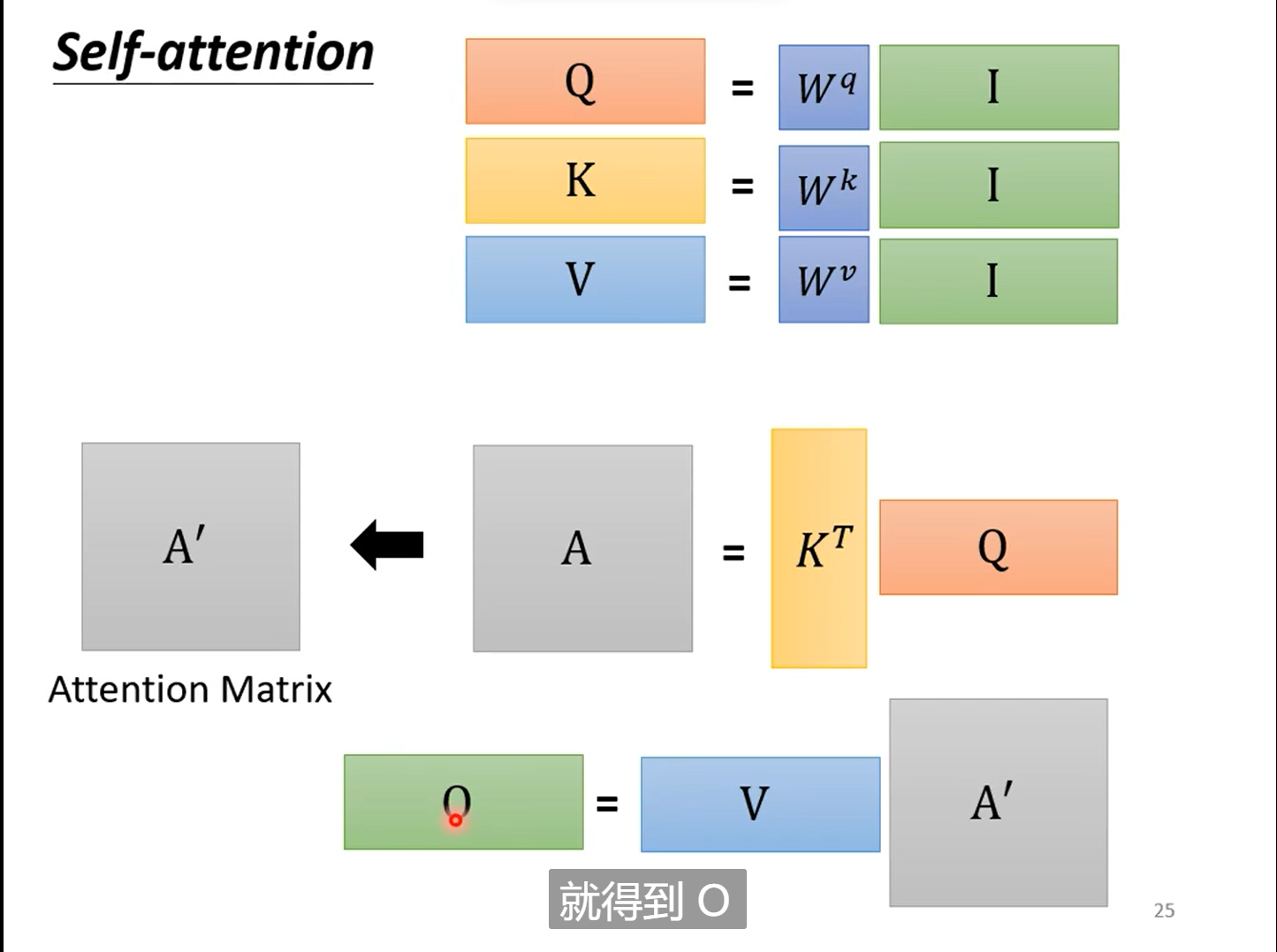
2.6.self-attention的矩阵表示

1	2

3	4

分析:

这样看来self-attention其实就是一系列的矩阵乘法，看似复杂，其实真正未知的只有𝑊𝑞 和𝑊𝑘以及𝑊𝑣，这三个矩阵参数需要学习。

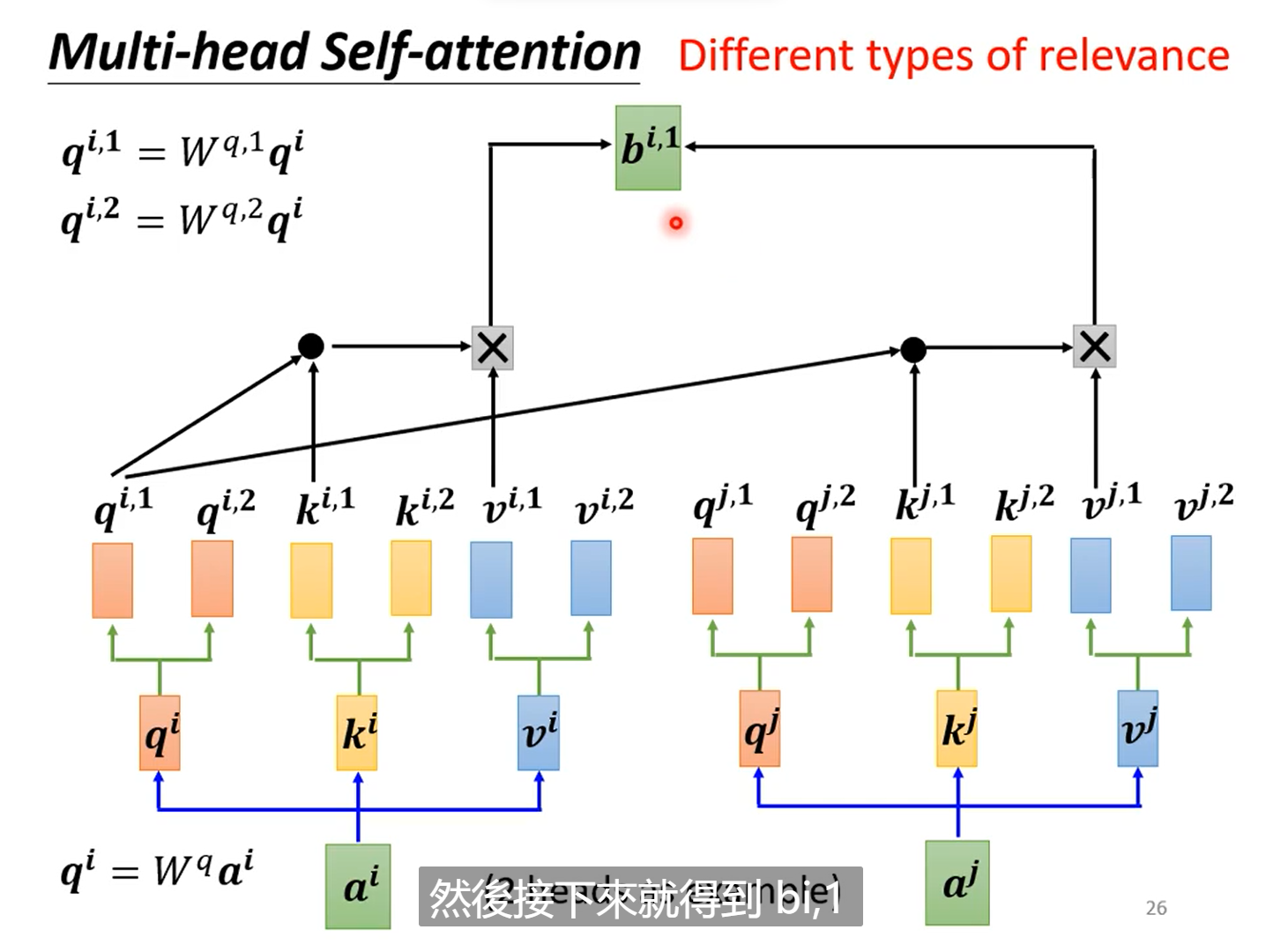
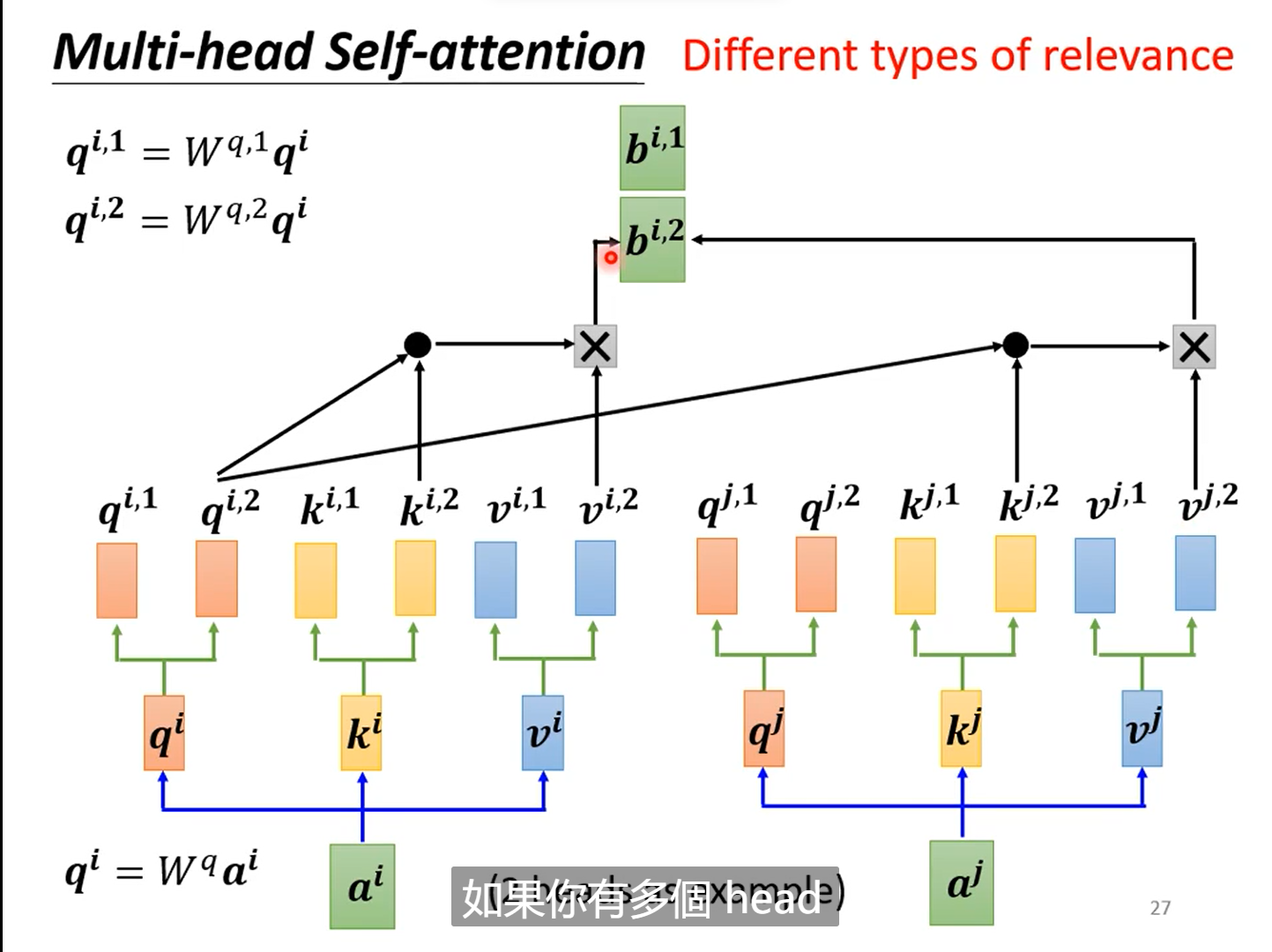
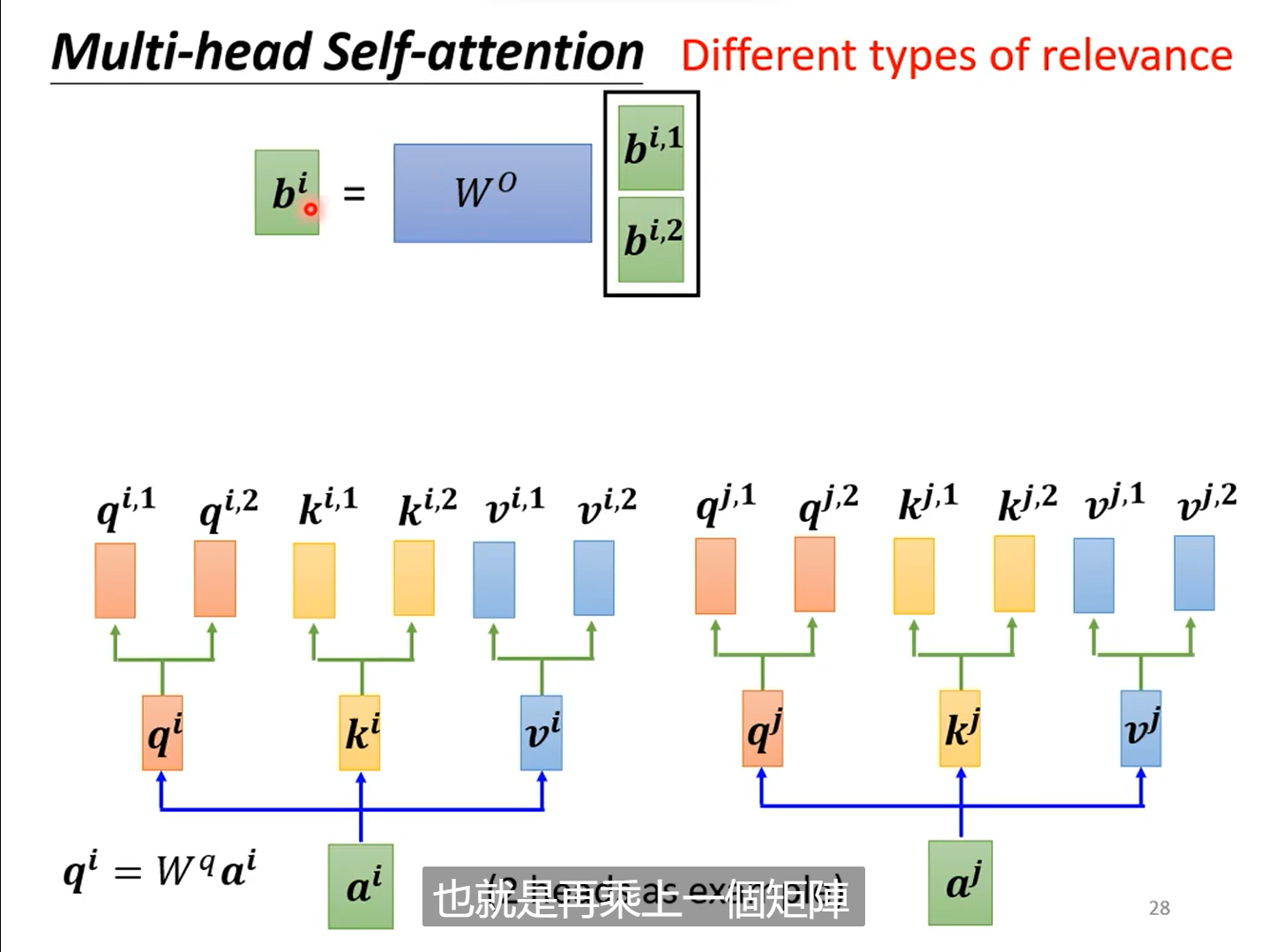
2.7多头注意力Multi-head-attention

本质上在self-attention中，我们使用的是单个q,k去寻找两个向量之间的关系，但是当关系有多种时，我们应该去使用多个q,和多个K来计算他们的多个相关性。

例如：当计算两个attention时有，有如下步骤

1	2

3	4

三、self-attention与CNN以及RNN的对比

3.1.self attention 与 CNN

由于self-attention考虑的是一整个图像的讯息，而CNN考虑到的是感受野里面的讯息，所以我们可以说CNN是简化版的self-attention,而self-attention是更复杂的CNN。

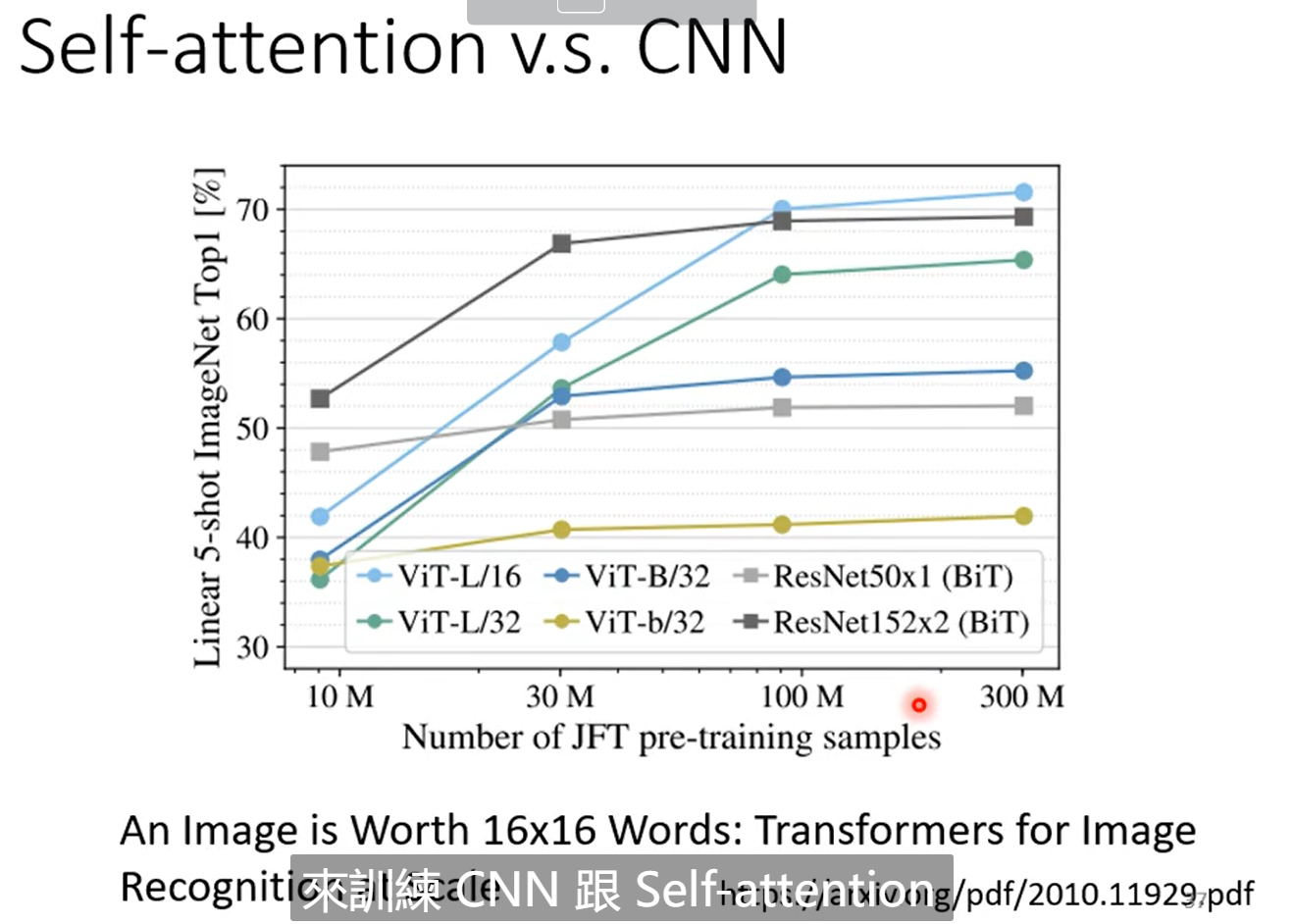
由于CNN是更简单的模型，因此CNN相比self attention更适合在小的数据量上进行训练，而self attention 更适合在大的数据量上训练，下面这张表显示了在不同的数据量卷积模型和注意力机制的模型效果。在数据量更大的时候，看到self attention 的效果是好于CNN的。

3.2.self attention 与RNN

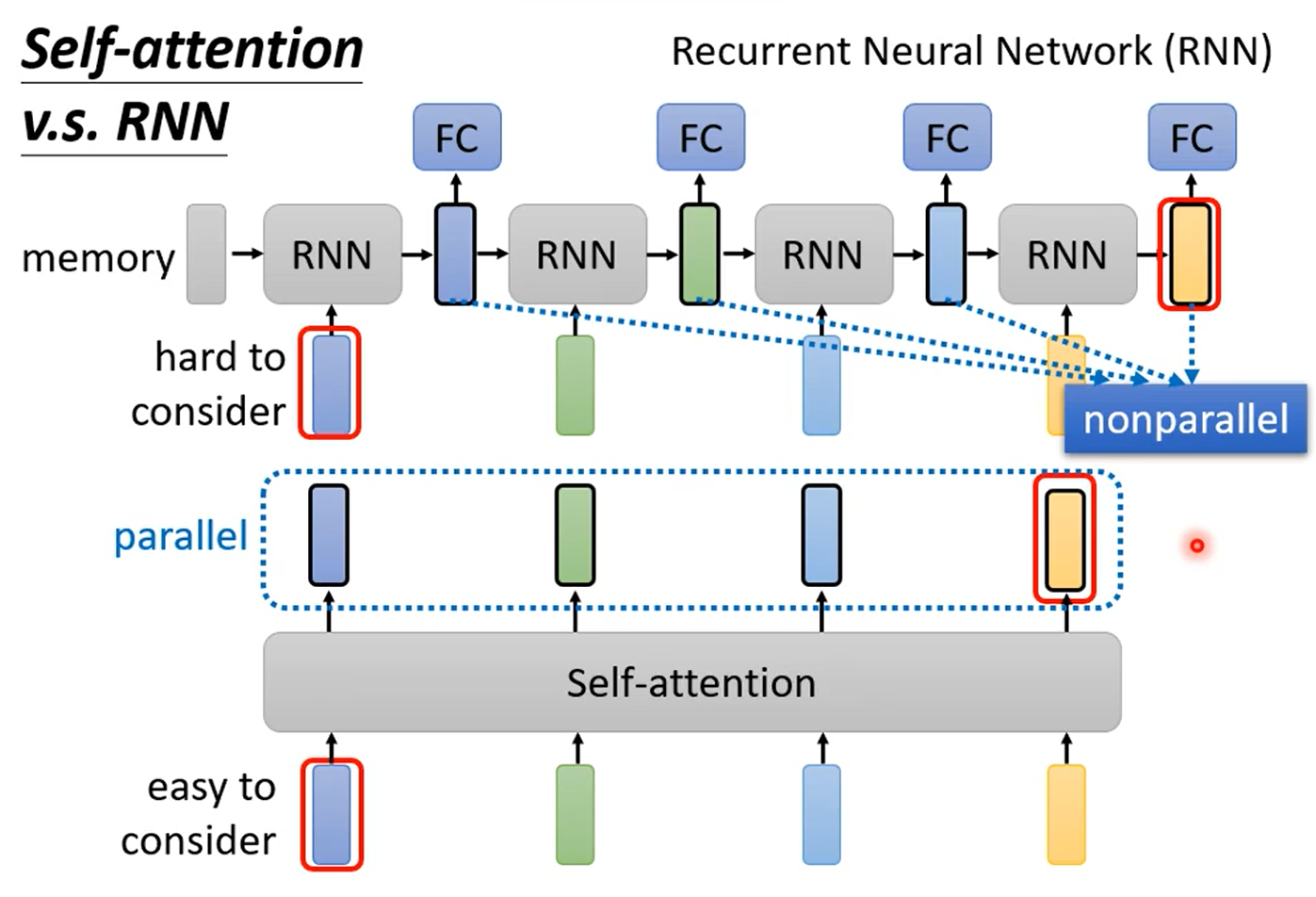
与RNN相比，self attention有两个明显的优势，一个就是self-attention可以平行化处理，而RNN必须等前面的处理完才能继续处理。另外一个优势就是RNN更难考虑真个向量序列的信息，不同的向量之间存在远近的关系，而self attention更容易考虑整个向量序列的向量之间的关系，因为不同的向量之间是“等距的”。