当前位置：首页 > article >正文

如何在Unity中实现AStar寻路算法及地图编辑器

article 2024/12/28 2:32:48

文章目录

AStar算法
- 简介
- 实现
- - Node节点
  - 节点间的估价
  - 算法核心
  - 邻节点的搜索方式
地图编辑器
- 简介
- 实现
- - 绘制地图网格
  - 障碍/可行走区域
  - 地图数据存储

AStar算法

AStar 寻路

简介

Unity中提供了NavMesh导航寻路的AI功能，如果项目不涉及服务端它应该能满足大部分需求，但如果涉及服务端且使用状态同步技术，可能需要服务端同时实现寻路功能，这时就需要考虑其它实现思路，而AStar寻路算法则是常使用的一种。

AStar算法是一种静态路网中求解最短路径最有效的直接搜索方法，基于广度优先搜索（BFS）和Dijkstra算法，通过不断维护节点的代价来寻求代价最小的路径，代价的估价公式：F(N)=G(N) + H(N)。

G：理解为起始节点到当前节点的代价；
H：理解为当前节点到终节点的代价。

其它概念：

开放集合：记录所有被考虑用来寻找最短路径的节点集合；
封闭集合：记录不会被考虑用来寻找最短路径的节点集合。

算法思路：

将起始节点放入开放集合；
While循环重复以下步骤，直到结束条件满足：
- 在开放集合中寻找代价最小的节点，并把寻找到的节点作为Current当前节点；
- 将获取到的当前节点从开放集合移除放入封闭集合；
- 若当前节点已经是终节点，寻路结束，跳出While循环，否则继续执行以下操作；
- 获取当前节点的邻节点，并对每个邻节点执行以下步骤：
  - 若邻节点为不可行走区域(障碍)或者邻节点已经在封闭集合中，不执行任何操作，Continue继续遍历下一个邻节点；
  - 若邻节点不在开放集合中，将其放入开放集合，并将Current当前节点赋值给该邻节点的父节点，计算、记录该邻节点的G、H代价；
  - 若邻节点在开放集合中，判断经Current当前节点到达该邻节点的G值是否小于原来的G值，若小于则将该邻节点的父节点设为当前节点，并重新计算该邻节点的G、H代价。
从终节点开始依次获取父节点放入一个列表，最终将列表做倒序操作就是最终寻路的路径。

实现

Node节点

地图网格由x * y个Node节点组成，定义节点类，变量包含节点的x、y索引值、父节点信息、G、H、F代价值以及是否为可行走区域的标识信息，代码如下：

namespace SK.Framework.AStar
{
    public class Node
    {
        public int x;
        public int y;

        /// <summary>
        /// 父节点
        /// </summary>
        public Node parent;
        /// <summary>
        /// 是否为可行走区域
        /// </summary>
        public bool IsWalkable { get; private set; }
        /// <summary>
        /// 起始节点到当前节点的代价
        /// </summary>
        public int gCost;
        /// <summary>
        /// 当前节点到终节点的代价
        /// </summary>
        public int hCost;
        /// <summary>
        /// 代价
        /// </summary>
        public int Cost { get { return gCost + hCost; } }

        public Node(int x, int y, bool isWalkable)
        {
            this.x = x;
            this.y = y;
            IsWalkable = isWalkable;
        }
    }
}

节点间的估价

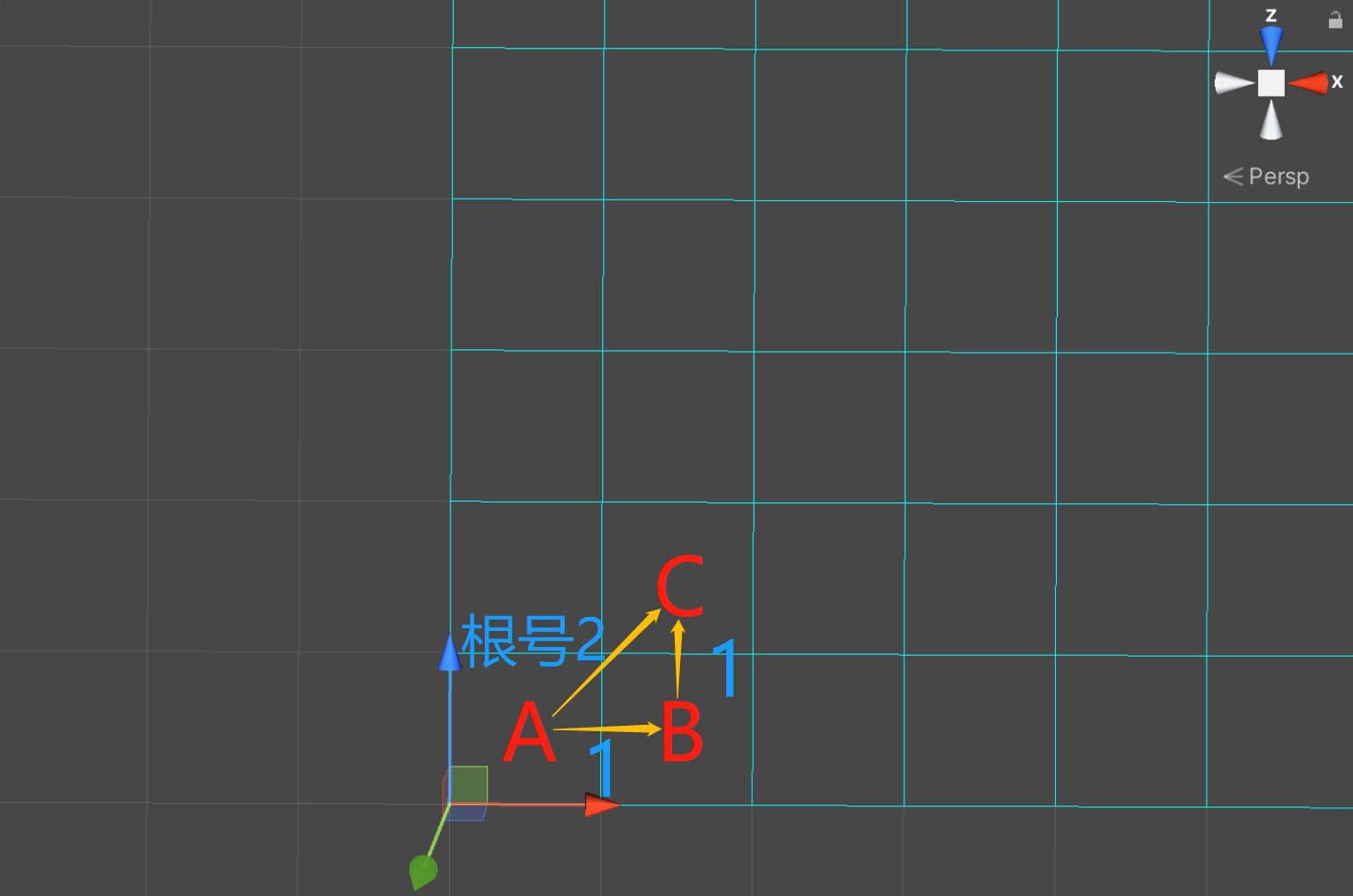
每向正上、下、左右方向走一步代价为1，根据勾股定理，每向斜方向走一步代价为 $\sqrt{2}$ ，近似1.414，而为了便于计算、节省性能，我们将正方向移动一步的代价记为10，斜方向移动一步的代价记为14，都取int整数。

估价方式

//计算两节点之间的代价
private int CalculateCost(Node n1, Node n2)
{
    //绝对值
    int deltaX = n1.x - n2.x;
    if (deltaX < 0) deltaX = -deltaX;
    int deltaY = n1.y - n2.y;
    if (deltaY < 0) deltaY = -deltaY;
    int delta = deltaX - deltaY;
    if (delta < 0) delta = -delta;
    //每向正上、下、左、右方向走一步代价增加10
    //每斜向走一步代价增加14(勾股定理，精确来说是近似14.14~)
    return 14 * (deltaX > deltaY ? deltaY : deltaX) + 10 * delta;
}

算法核心

/// <summary>
/// 根据起始节点和终节点获取路径
/// </summary>
/// <param name="startNode">起始节点</param>
/// <param name="endNode">终节点</param>
/// <returns>路径节点集合</returns>
public List<Node> GetPath(Node startNode, Node endNode)
{
    //开放集合
    List<Node> openCollection = new List<Node>();
    //封闭集合
    HashSet<Node> closeCollection = new HashSet<Node>();
    //起始节点放入开放集合
    openCollection.Add(startNode);
    //开放集合中数量为0时 寻路结束
    while (openCollection.Count > 0)
    {
        //当前节点
        Node currentNode = openCollection[0];
        //遍历查找是否有代价更小的节点
        //若代价相同，选择移动到终点代价更小的节点
        for (int i = 1; i < openCollection.Count; i++)
        {
            currentNode = (currentNode.Cost > openCollection[i].Cost
                || (currentNode.Cost == openCollection[i].Cost
                && currentNode.hCost > openCollection[i].hCost))
                ? openCollection[i] : currentNode;
        }
        //将获取到的当前节点从开放集合移除放入封闭集合
        openCollection.Remove(currentNode);
        closeCollection.Add(currentNode);
        //当前节点已经是终节点 寻路结束
        if (currentNode == endNode)
            break;
        //获取邻节点
        List<Node> neighbourNodes = GetNeighbouringNodes(currentNode, SearchMode.Link8);
        //在当前节点向邻节点继续搜索
        for (int i = 0; i < neighbourNodes.Count; i++)
        {
            Node neighbourNode = neighbourNodes[i];
            //判断邻节点是否为不可行走区域(障碍)或者邻节点已经在封闭集合中
            if (!neighbourNode.IsWalkable || closeCollection.Contains(neighbourNode))
                continue;

            //经当前节点到达该邻节点的G值是否小于原来的G值
            //或者该邻节点还没有放入开放集合，将其放入开放集合
            int cost = currentNode.gCost + CalculateCost(currentNode, neighbourNode);
            if (cost < neighbourNode.gCost || !openCollection.Contains(neighbourNode))
            {
                neighbourNode.gCost = cost;
                neighbourNode.hCost = CalculateCost(neighbourNode, endNode);
                neighbourNode.parent = currentNode;
                if (!openCollection.Contains(neighbourNode))
                    openCollection.Add(neighbourNode);
            }
        }
    }

    //倒序获取父节点
    List<Node> path = new List<Node>();
    Node currNode = endNode;
    while (currNode != startNode)
    {
        path.Add(currNode);
        currNode = currNode.parent;
    }
    //再次倒序后得到完整路径
    path.Reverse();
    return path;
}

邻节点的搜索方式

搜索邻节点时有两种搜索方式，四连通和八连通：

四连通：又称四邻域，是指对应节点的上、下、左、右四个方向为邻节点：

四连通

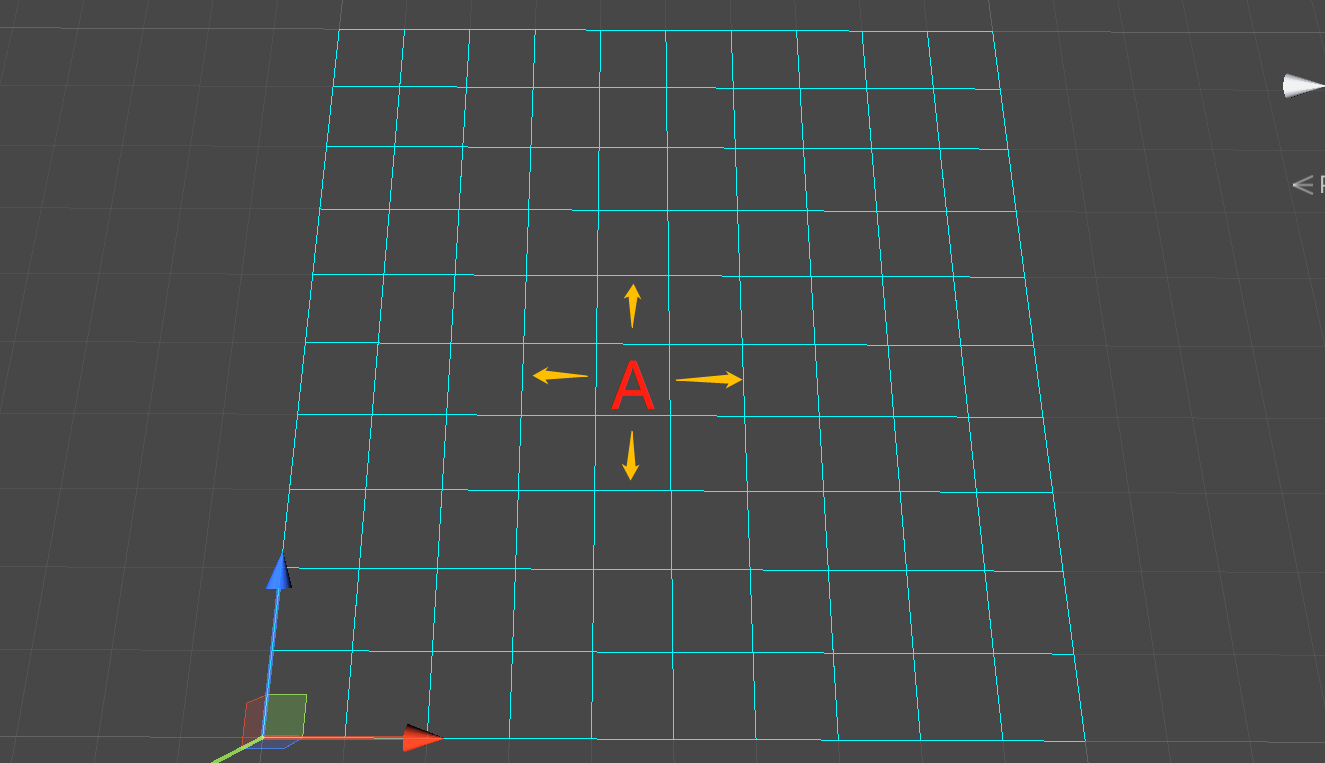
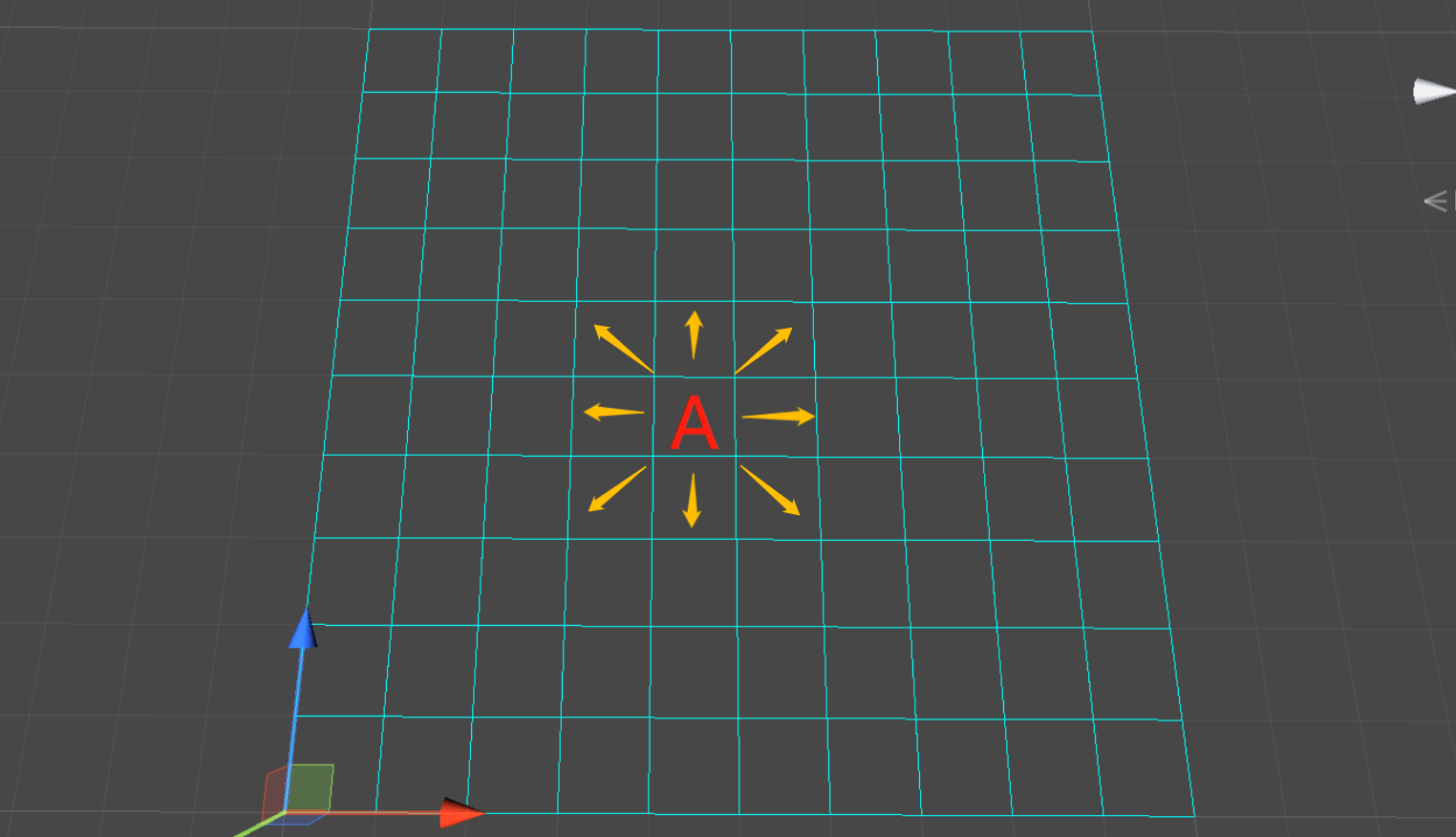
八连通：又称八邻域，是指对应节点的上、下、左、右、左上、右上、左下、右下八个方向为邻节点：

八连通

/// <summary>
/// 获取指定节点的邻节点
/// </summary>
/// <param name="node">指定节点</param>
/// <param name="searchMode">搜索方式 四连通/八连通</param>
/// <returns>邻节点列表</returns>
public List<Node> GetNeighbouringNodes(Node node, SearchMode searchMode)
{
    List<Node> neighbours = new List<Node>();
    switch (searchMode)
    {
        case SearchMode.Link4:
            for (int i = -1; i <= 1; i++)
            {
                if (i == 0) continue;
                int x = node.x + i;
                if (x >= 0 && x < this.x)
                    neighbours.Add(nodesDic[x * this.x + node.y]);
                int y = node.y + i;
                if (y >= 0 && y < this.y)
                    neighbours.Add(nodesDic[node.x * this.x + y]);
            }
            break;
        case SearchMode.Link8:
            for (int i = -1; i <= 1; i++)
            {
                for (int j = -1; j <= 1; j++)
                {
                    if (i == 0 && j == 0) continue;
                    int x = node.x + i;
                    int y = node.y + j;
                    if (x >= 0 && x < this.x && y >= 0 && y < this.y)
                        neighbours.Add(nodesDic[x * this.x + y]);
                }
            }
            break;
    }
    return neighbours;
}

地图编辑器

简介

Map Editor

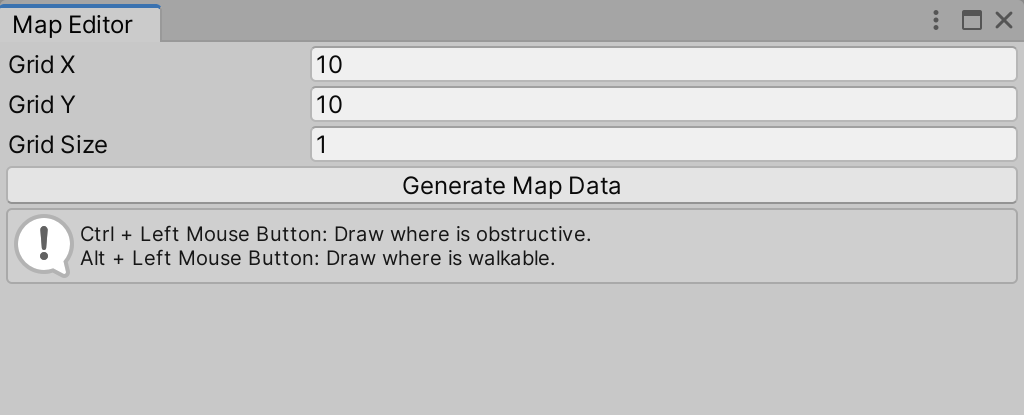
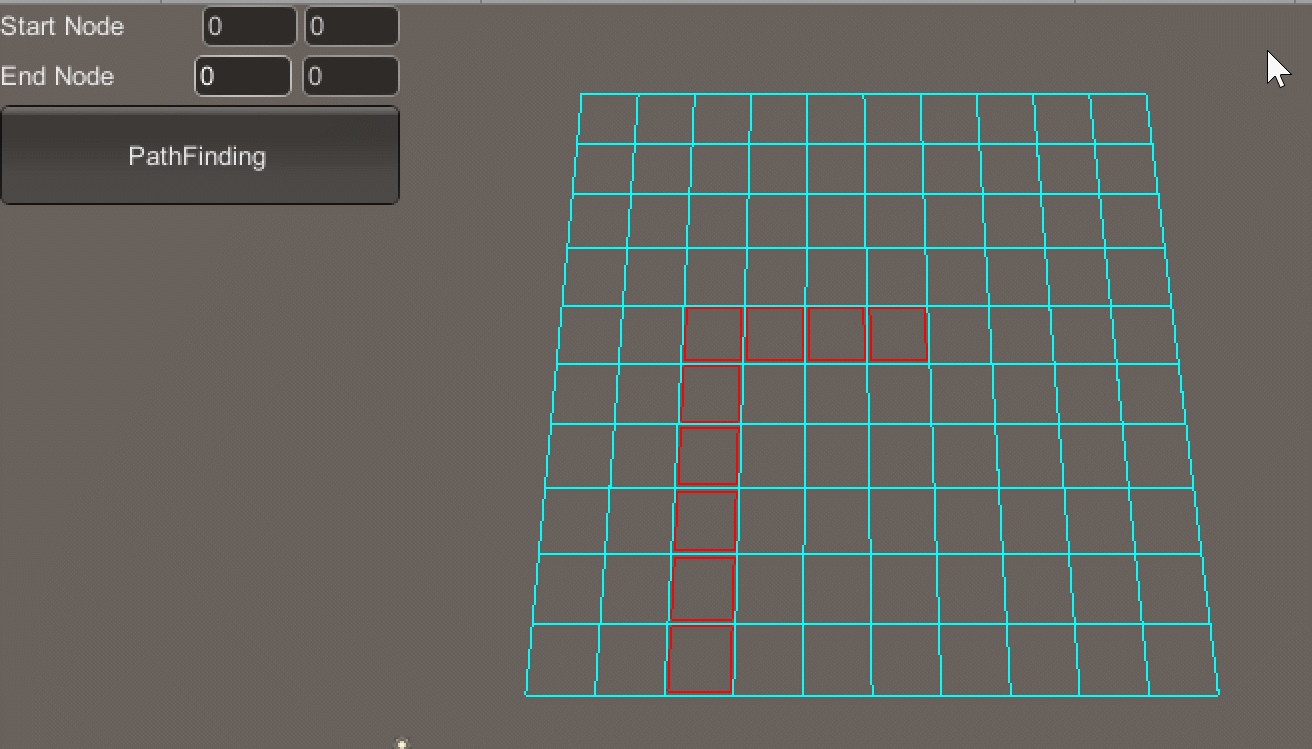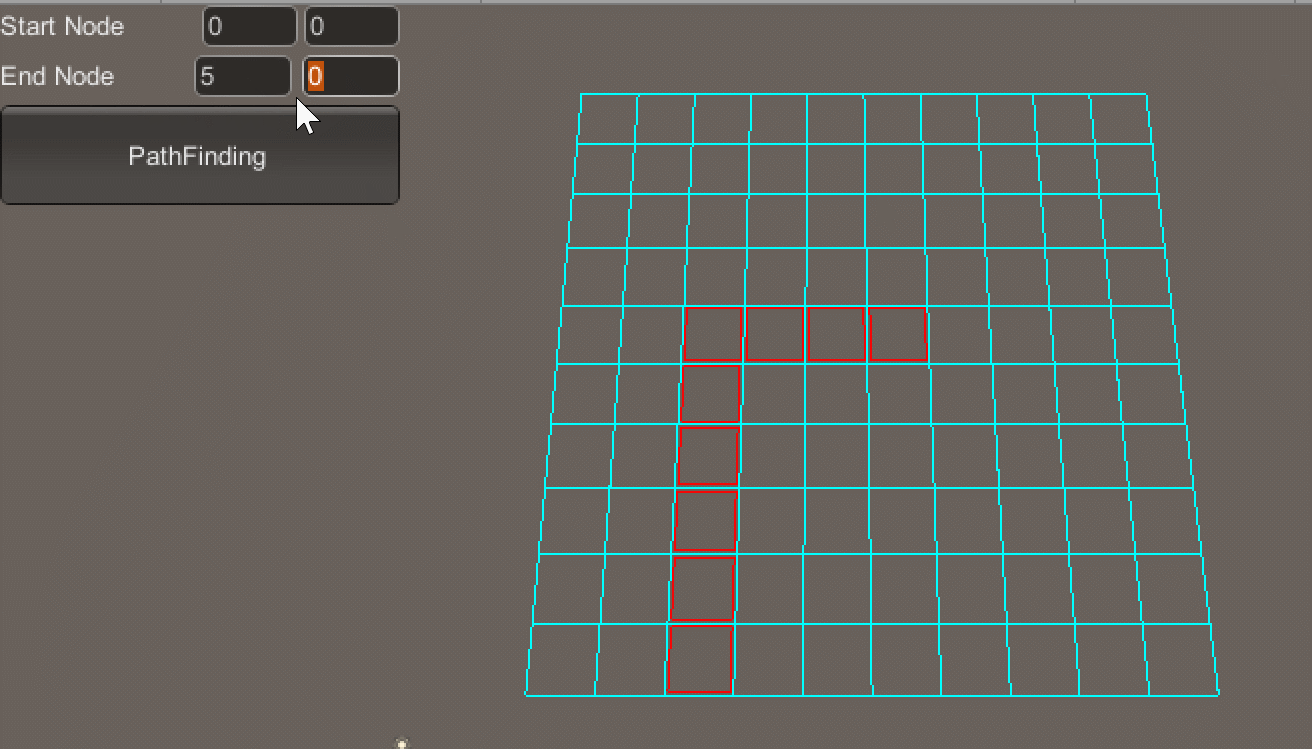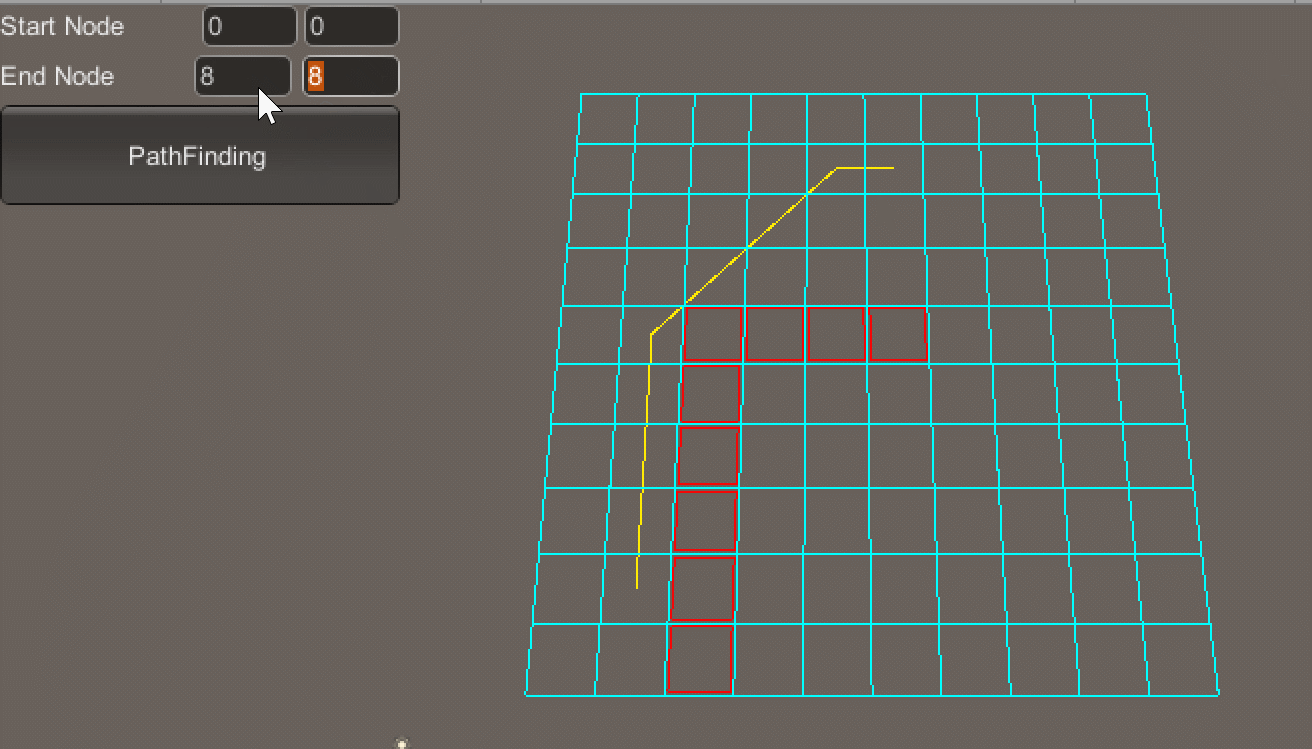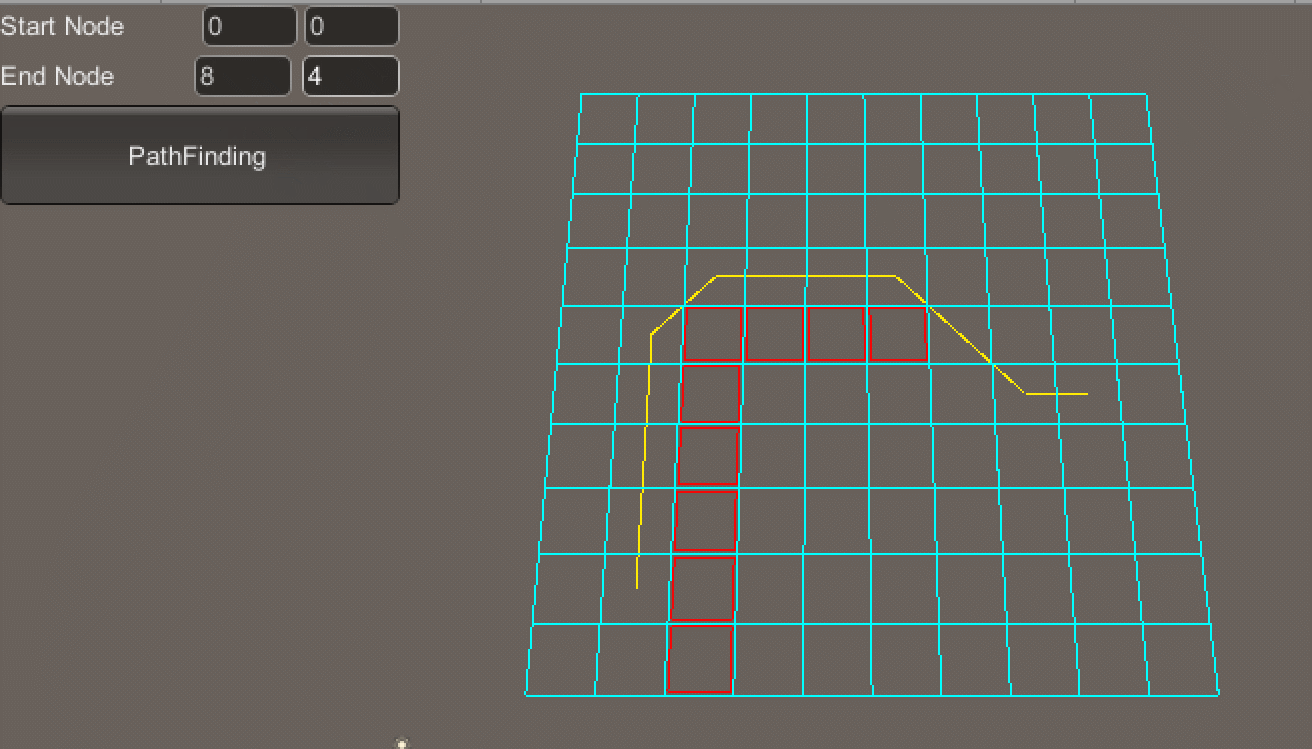
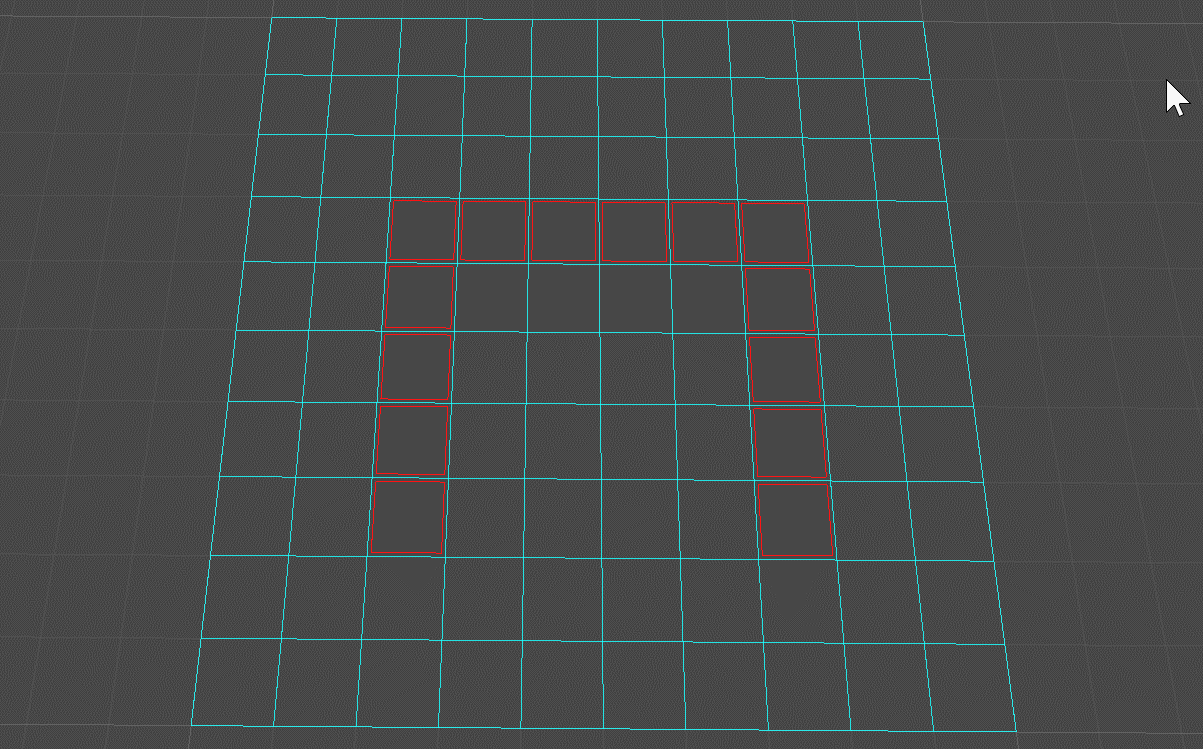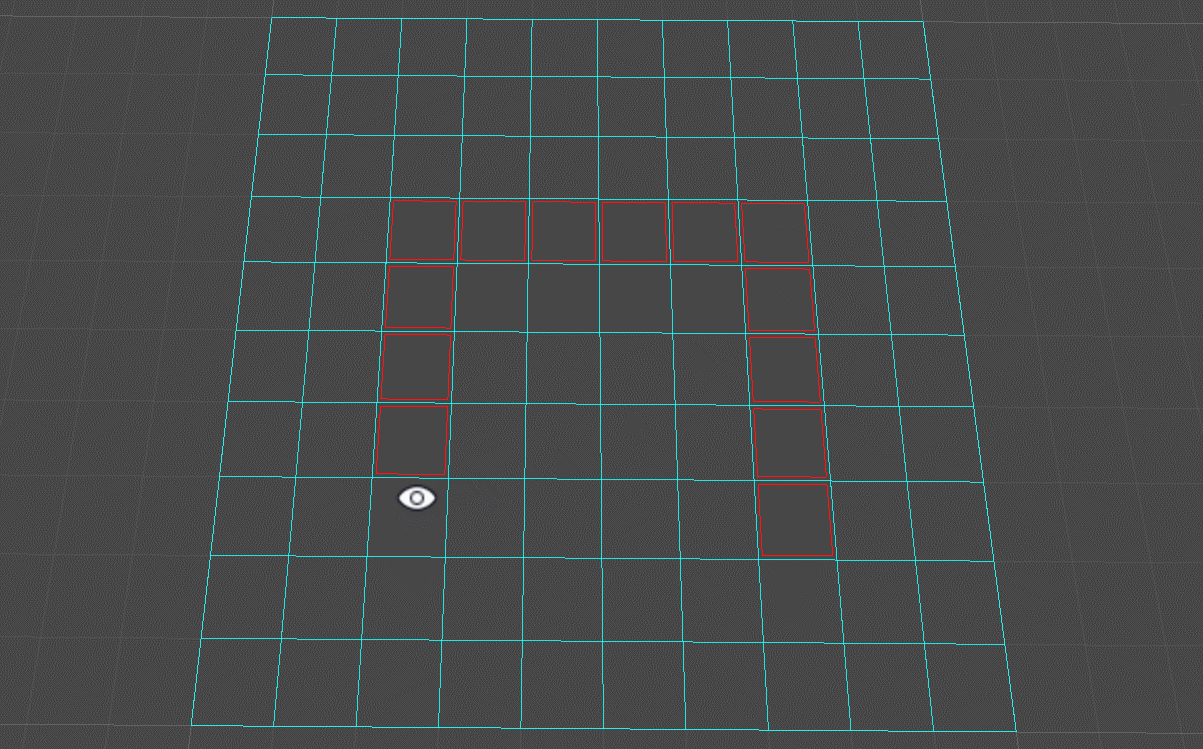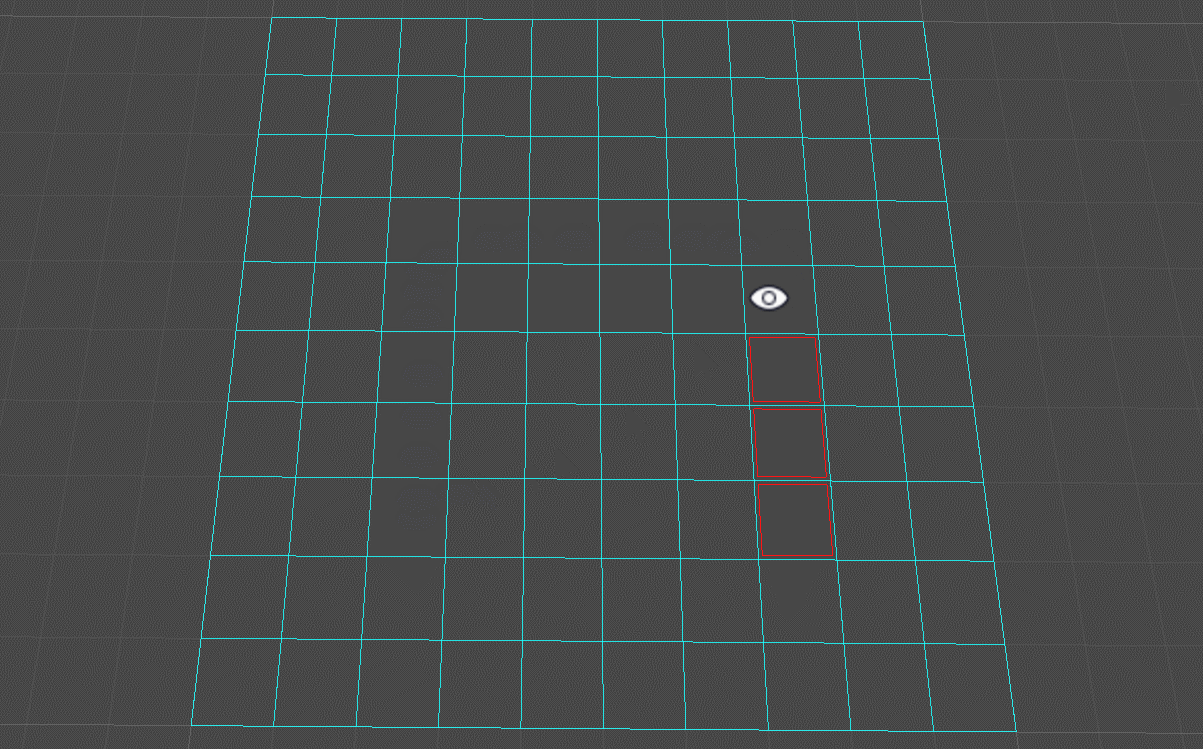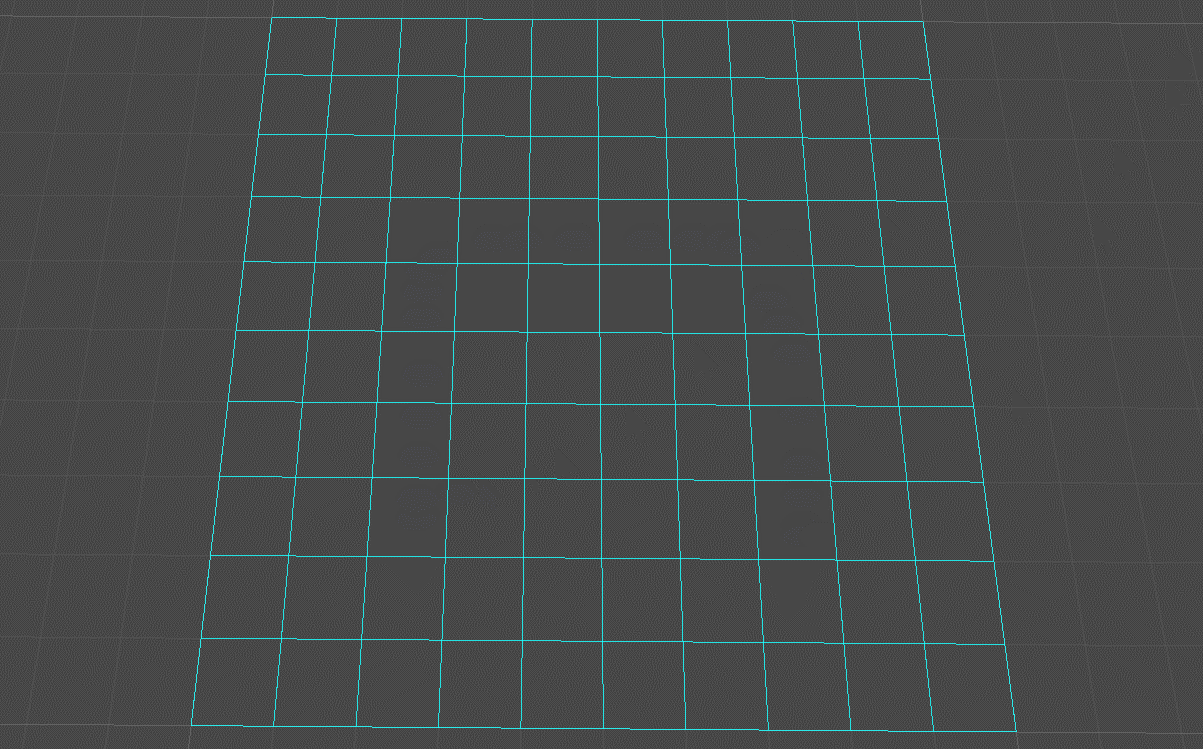
按住Ctrl + 鼠标左键绘制地图障碍区域（如图所示，红色框区域即为障碍区域）：

绘制障碍区域

按住Alt + 鼠标左键绘制地图可行走区域（清除障碍区域）：

绘制可行走区域

实现

绘制地图网格

Grid X、Y组成地图网格（x * y）；
Grid Size指定每个网格(节点)的大小：

//绘制地图网格
Handles.color = Color.cyan;
for (int i = 0; i <= x; i++)
{
    Vector3 start = i * size * Vector3.right;
    Vector3 end = start + y * size * Vector3.forward;
    Handles.DrawLine(start, end);
}
for (int i = 0; i <= y; i++)
{
    Vector3 start = i * size * Vector3.forward;
    Vector3 end = start + x * size * Vector3.right;
    Handles.DrawLine(start, end);
}

障碍/可行走区域

使用二维数组bool[,] map存储各节点网格是否为可行走区域

Ctrl + 鼠标左键 标识障碍区域；
Alt + 鼠标左键 标识可行走区域：

HandleUtility.AddDefaultControl(GUIUtility.GetControlID(FocusType.Passive));
//Ctrl + 鼠标左键 绘制障碍区域
//Alt + 鼠标左键 绘制可行走区域
var e = Event.current;
if (e != null && (e.control || e.alt) && (e.type == EventType.MouseDown || e.type == EventType.MouseDrag) && e.button == 0)
{
    Ray ray = HandleUtility.GUIPointToWorldRay(e.mousePosition);
    if (Physics.Raycast(ray, out RaycastHit hit))
    {
        int targetX = Mathf.CeilToInt(hit.point.x / size);
        int targetY = Mathf.CeilToInt(hit.point.z / size);
        if (targetX <= x && targetX > 0 && targetY <= y && targetY > 0)
        {
            map[targetX - 1, targetY - 1] = !e.control;
        }
    }
    e.Use();
}

//红色框绘制障碍区域
Handles.color = Color.red;
for (int m = 0; m < x; m++)
{
    for (int n = 0; n < y; n++)
    {
        if (!map[m, n])
            Handles.DrawWireCube(new Vector3(m * size, 0f, n * size) + .5f * size * (Vector3.forward + Vector3.right), .9f * size * (Vector3.forward + Vector3.right));
    }
}

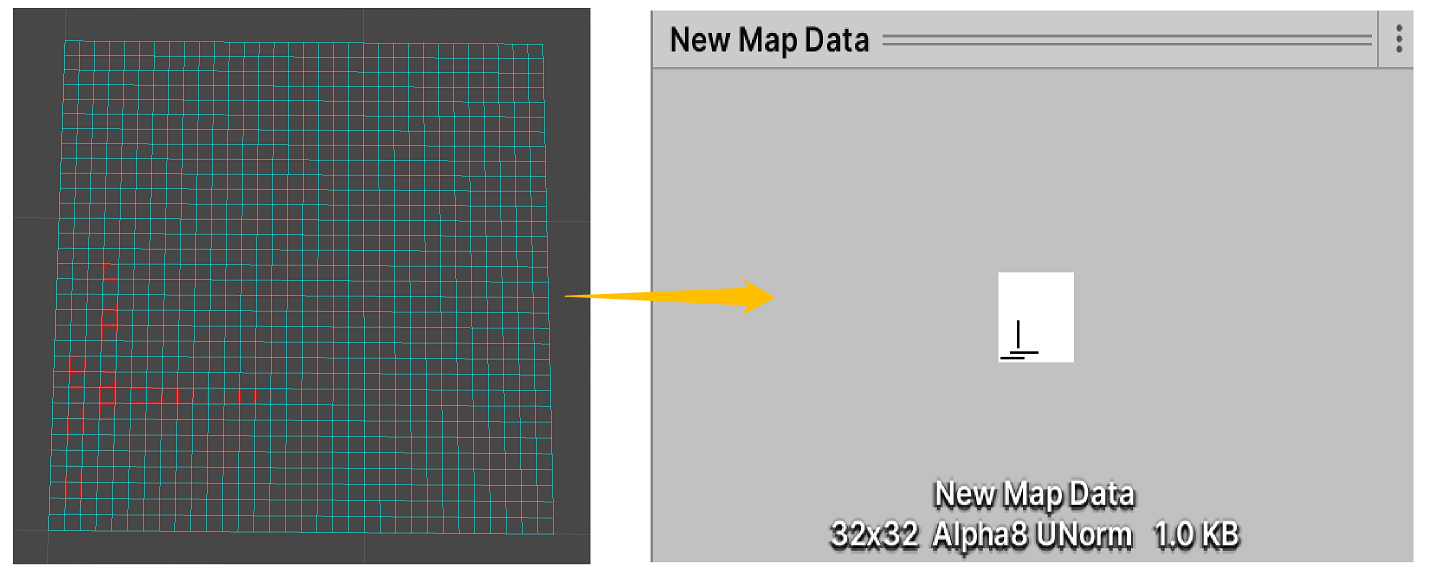
地图数据存储

由于地图数据存储于bool[,] map二维数组中，不支持序列化，因此将其转化为存储于Texture2D类型资产中，实现方式如下：

//生成地图
if (GUILayout.Button("Generate Map Data"))
{
    //选择保存路径
    string filePath = EditorUtility.SaveFilePanel("Save Map Data", Application.dataPath, "New Map Data", "asset");
    if (!string.IsNullOrEmpty(filePath))
    {
        //转化为Asset路径
        filePath = filePath.Substring(filePath.IndexOf("Assets"));
        //创建地图Tex
        Texture2D bitmap = new Texture2D(x, y, TextureFormat.Alpha8, false);
        byte[] bytes = bitmap.GetRawTextureData();
        //默认全部为可行走区域
        for (int i = 0; i < bytes.Length; i++)
            bytes[i] = 0;
        for (int m = 0; m < x; m++)
        {
            for (int n = 0; n < y; n++)
            {
                //黑色存储障碍区域 白色存储可行走区域
                bytes[m * x + n] = (byte)(map[m, n] ? 255 : 0);
            }
        }
        bitmap.LoadRawTextureData(bytes);
        //创建、保存资产
        AssetDatabase.CreateAsset(bitmap, filePath);
        AssetDatabase.SaveAssets();
        AssetDatabase.Refresh();
        //选中
        EditorGUIUtility.PingObject(bitmap);
    }
}