当前位置：首页 > article >正文

回文数：探索数字世界中的对称美学

article 2024/9/21 5:41:28

在这里插入图片描述

本篇博客我会讲解力扣中的“9. 回文数”这道题，大家重点理解判断回文数的方法。

先来审题：这是题目链接。

在这里插入图片描述
来看几个输出示例：

还有一些条件：

第一反应是：为啥是个整数呢？万一是个字符串，那不简单了？只需2个指针，一个从左向右遍历，另一个从右向左遍历，相遇之前，如果对应的字符都相同，就是“回文串”。

所以，这道题可以使用sprintf或者itoa等函数，把整数先转换成字符串，再来解决。不过那样就太low了，而且“进阶”也说了，你能不将整数转换成字符串来解决这个问题吗？

所以，这里我们讨论的问题是：如何不把整数转换成字符串，直接判断它是不是回文数？

思路是这样的：如果一个数反过来还是它自己，那么这个数就是回文数。请仔细体会这句话。

下面的问题是：如何把一个数反过来？比如，把1234反过来变成4321？

大家可以联想以下，如何使用操作符操作整数。一个比较经典的操作是：取出每一位，用的是“%10 /10”的思路。

1234 % 10 = 4
1234 / 10 = 123
123 % 10 = 3
123 / 10 = 12
12 % 10 = 2
12 / 10 = 1
1 % 10 = 1
1 / 10 = 0

在这个数变成0之前，我们就从后向前把每一位拿出来了，也就是拿到了4、3、2、1。看起来好像倒过来了？

不完全是。现在，我们还要把它们存到一个新的数中，也就是让一个整型变量rev里面存的是4321。怎么存呢？

很简单，每次执行rev = rev * 10 + 某个一位数;即可。也就是：

rev = 0
rev = rev * 10 + 1;
rev = 1
rev = rev * 10 + 2;
rev = 12
rev = rev * 10 + 3;
rev = 123
rev = rev * 10 + 4;
rev = 1234

把上面的思路整合一下：每次“%10 /10”拿到每一位，再用“某个变量乘10加上这个数”的方式把这一位数存进去，就能把一开始的数倒过来了。如果倒过来的数就是它本身，那么就是回文数。

注意：由于“把x倒过来”的操作会修改x，所以先用tmp拷贝一份，再把tmp倒过来即可。

写成代码如下：

bool isPalindrome(int x){
    // 把x倒过来
    int rev = 0;
    int tmp = x;
    while (tmp)
    {
        // 把tmp的最右边一位数存到rev里
        rev = rev*10 + (tmp%10);
        // 去掉tmp的最右边一位
        tmp /= 10;
    }

    return rev == x;
}

但是这样会有用例过不了：
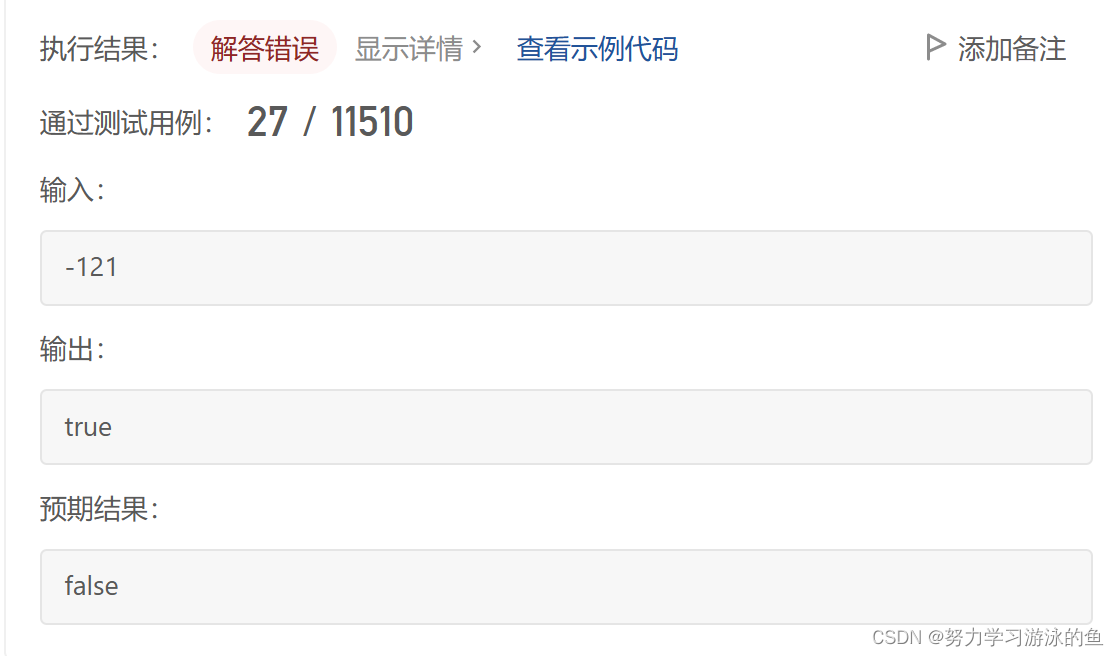
在这里插入图片描述
分析一下：我们的操作都是针对正数的，负数肯定不是回文数，直接return false即可。

bool isPalindrome(int x){
    // 负数不是回文数
    if (x < 0)
        return false;
    
    // 把x倒过来
    int rev = 0;
    int tmp = x;
    while (tmp)
    {
        // 把tmp的最右边一位数存到rev里
        rev = rev*10 + (tmp%10);
        // 去掉tmp的最右边一位
        tmp /= 10;
    }

    return rev == x;
}

但是还是有用例过不了：
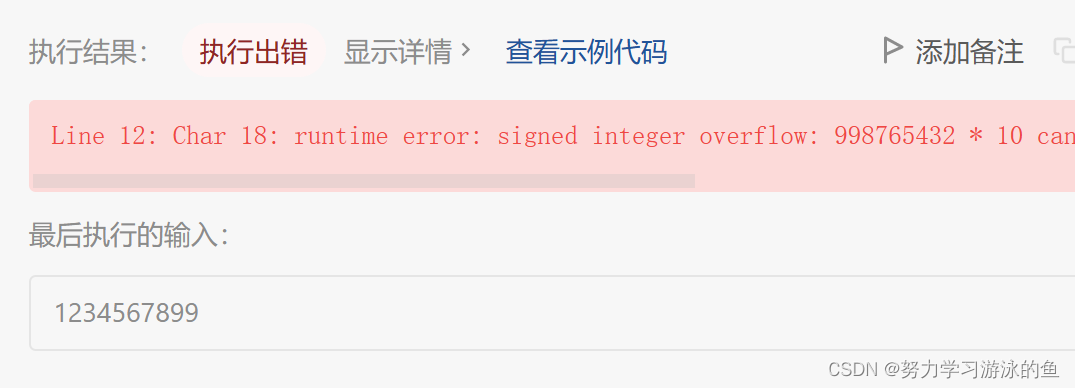
在这里插入图片描述
如果你有经验的话，会发现这个数好大！可能越界了，所以不能用int来存储，应该改成long或者long long，这里先用long试一下：

bool isPalindrome(int x){
    // 负数不是回文数
    if (x < 0)
        return false;
    
    // 把x倒过来
    long rev = 0;
    long tmp = x;
    while (tmp)
    {
        // 把tmp的最右边一位数存到rev里
        rev = rev*10 + (tmp%10);
        // 去掉tmp的最右边一位
        tmp /= 10;
    }

    return rev == x;
}

在这里插入图片描述

这样就过了。

接下来优化一下这个思路：其实只需要反转后半段就行了。比如：1221，只需反转后半段，变成1212，此时前半段和后半段相同，是回文数。再比如：12321，反转后半段，成为12123，由于12==123/10，也是回文数。

注意考虑一些特殊情况：负数不是回文数，最后一位是0也不是回文数（0除外）。

代码如下：

bool isPalindrome(int x){
    // 回文数不是负数
    if (x < 0)
        return false;

    // 回文数最后一位不是0（0本身除外）
    if (x%10 == 0 && x)
        return false;

    // 反转后半段
    int rev = 0;
    while (x > rev)
    {
        rev = rev*10 + (x%10);
        x /= 10;
    }
    return rev==x || x==rev/10;
}