LeetCode 1206. 实现跳表
不使用任何库函数,设计一个跳表。
跳表是在 O(log(n)) 时间内完成增加、删除、搜索操作的数据结构。跳表相比于树堆与红黑树,其功能与性能相当,并且跳表的代码长度相较下更短,其设计思想与链表相似。
例如,一个跳表包含 [30, 40, 50, 60, 70, 90],然后增加 80、45 到跳表中,以下图的方式操作:
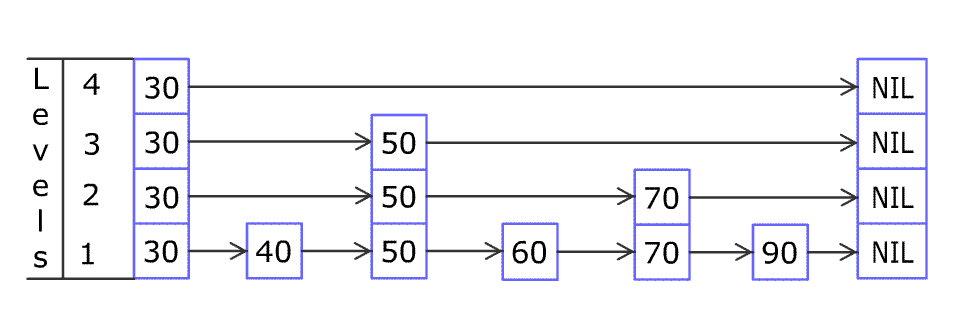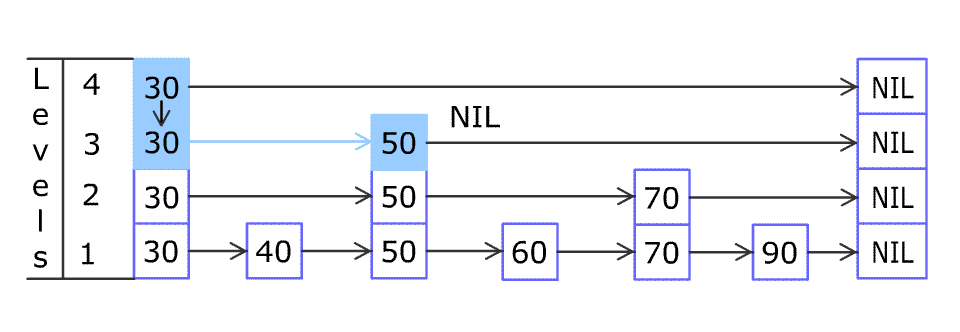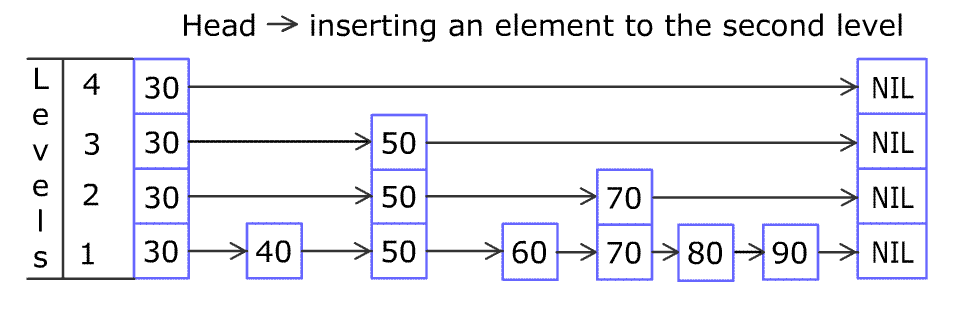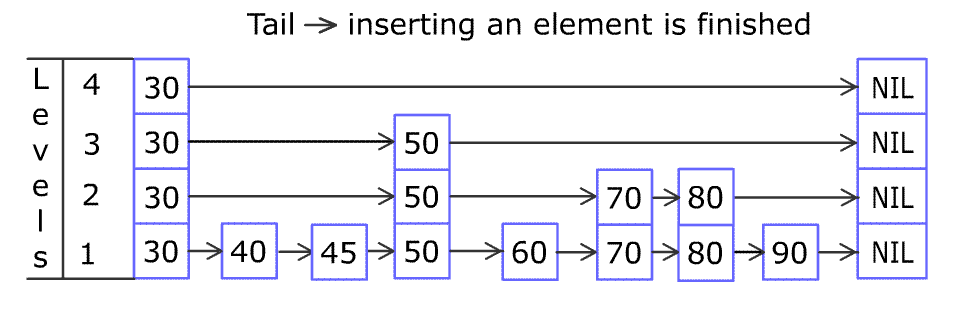
跳表中有很多层,每一层是一个短的链表。在第一层的作用下,增加、删除和搜索操作的时间复杂度不超过 O(n)。跳表的每一个操作的平均时间复杂度是 O(log(n)),空间复杂度是 O(n)。
注意,跳表中可能存在多个相同的值,你的代码需要处理这种情况。
题目分析
跳表其实就是加了几层索引的链表,一共有 N 层,以 0 ~ N-1 层表示,设第 0 层是原链表,抽取其中部分元素,在第 1 层形成新的链表,上下层的相同元素之间连起来;再抽取第 1 层部分元素,构成第 2 层,以此类推。
为什么需要random函数呢?
需要某种手段来维护索引与原始链表大小之间的平衡,也就是说,如果链表中结点多了,索引结点就相应地增加一些,避免复杂度退化,以及查找、插入、删除操作性能下降。
如果你了解红黑树、AVL 树这样平衡二叉树,你就知道它们是通过左右旋的方式保持左右子树的大小平衡,而跳表是通过随机函数来维护前面提到的“平衡性”。
【查找】
跳表其实就是加了几层索引的链表,一共有 N 层,以 0 ~ N-1 层表示,设第 0 层是原链表,抽取其中部分元素,在第 1 层形成新的链表,上下层的相同元素之间连起来;再抽取第 1 层部分元素,构成第 2 层,以此类推。
具体选哪些元素呢?题目给的是coinFlip,也就是每次插入元素的时候,都进行一次 50% 概率的判断,如果 true 则向上层添加一个索引,如果 false 就不加了。
【添加和删除】
添加和删除的时候,存在数据重复的问题,经过我的测试,发现题目要求的是,将重复的数据当做不同的值来对待,即存了一个元素 9 ,再存一个 9 ,此时表里有俩 9 ,相互独立,删除一个 9 ,表里应该还剩余有一个9。
由于添加和删除元素都是从底层开始,而在查找的时候是从顶层开始查找的,因此可以使用一个数组记录每层的“跳跃节点”的位置,就不必反复的从顶层开始查找每层的位置了。
在添加的时候,首先是查找到添加位置,过程与查找类似,首先找到表中 >= 插入元素 的最小节点位置,然后插入节点, 50% 概率判别,如果需要添加索引,就添加索引,继续 50% 概率判别,直到结束。
在删除的时候,首先也是查找,找到表中所有 = 插入元素的节点位置(每层只找一个,找到直接跳层即可),然后挨个删除。
代码实现
class Skiplist {
class SkipListNode {
int val;
int cnt; // 当前val出现的次数
SkipListNode[] levels; // start from 0
SkipListNode() {
levels = new SkipListNode[MAX_LEVEL];
}
}
private double p = 0.5;
private int MAX_LEVEL = 16;
private SkipListNode head; // 头结点
private int level; //
private Random random;
public Skiplist() {
// 保存此level有利于查询(以及其他操作)
level = 0; // 当前 skiplist的高度(所有数字 level数最大的)
head = new SkipListNode();
random = new Random();
}
// 返回target是否存在于跳表中
public boolean search(int target) {
SkipListNode curNode = head;
for (int i = level-1; i >= 0; i--) {
while (curNode.levels[i] != null && curNode.levels[i].val < target) {
curNode = curNode.levels[i];
}
}
curNode = curNode.levels[0];
return (curNode != null && curNode.val == target);
}
// 插入一个元素到跳表。
public void add(int num) {
SkipListNode curNode = head;
// 记录每层能访问的最右节点
SkipListNode[] levelTails = new SkipListNode[MAX_LEVEL];
for (int i = level-1; i >= 0; i--) {
while (curNode.levels[i] != null && curNode.levels[i].val < num) {
curNode = curNode.levels[i];
}
levelTails[i] = curNode;
}
curNode = curNode.levels[0];
if (curNode != null && curNode.val == num) {
// 已存在,cnt 加1
curNode.cnt++;
} else {
// 插入
int newLevel = randomLevel();
if (newLevel > level) {
for (int i = level; i < newLevel; i++) {
levelTails[i] = head;
}
level = newLevel;
}
SkipListNode newNode = new SkipListNode();
newNode.val = num;
newNode.cnt = 1;
for (int i = 0; i < level; i++) {
newNode.levels[i] = levelTails[i].levels[i];
levelTails[i].levels[i] = newNode;
}
}
}
private int randomLevel() {
int level = 1; // 注意思考此处为什么是 1 ?
while (random.nextDouble() < p && level < MAX_LEVEL) {
level++;
}
return level > MAX_LEVEL ? MAX_LEVEL : level;
}
// 在跳表中删除一个值,如果 num 不存在,直接返回false. 如果存在多个 num ,删除其中任意一个即可。
public boolean erase(int num) {
SkipListNode curNode = head;
// 记录每层能访问的最右节点
SkipListNode[] levelTails = new SkipListNode[MAX_LEVEL];
for (int i = level-1; i >= 0; i--) {
while (curNode.levels[i] != null && curNode.levels[i].val < num) {
curNode = curNode.levels[i];
}
levelTails[i] = curNode;
}
curNode = curNode.levels[0];
if (curNode != null && curNode.val == num) {
if (curNode.cnt > 1) {
curNode.cnt--;
return true;
}
// 存在,删除
for (int i = 0; i < level; i++) {
if (levelTails[i].levels[i] != curNode) {
break;
}
levelTails[i].levels[i] = curNode.levels[i];
}
while (level > 0 && head.levels[level-1] == null) {
level--;
}
return true;
}
return false;
}
}
代码实现二
class Skiplist {
int MAX_LEVEL = 16;
int curLevel;
Node head;
public Skiplist() {
curLevel = 1;
head = new Node(-1);
head.next_point = new Node[MAX_LEVEL];
}
public boolean search(int target) {
Node temp = head;
//从最顶层索引找
for (int i = MAX_LEVEL - 1; i >=0; i--) {
while (temp.next_point[i] != null && temp.next_point[i].val <= target) {
if (temp.next_point[i].val == target)
return true;
else
temp = temp.next_point[i];
}
}
// 判断temp的下个节点是否满足条件
if (temp.next_point[0] != null && temp.next_point[0].val == target)
return true;
return false;
}
public void add(int num) {
int level = randomLevel(0.5);
if (level > curLevel)
curLevel = level;
Node node = new Node(num);
node.next_point = new Node[level];
Node[] forward = new Node[level];
Arrays.fill(forward, head);
Node temp = head;
// 找到前驱节点
for (int i = level - 1; i >= 0; i--) {
while (temp.next_point[i] != null && temp.next_point[i].val < num)
temp = temp.next_point[i];
forward[i] = temp;
}
// 更新连接
for (int i = 0; i < level; i++) {
node.next_point[i] = forward[i].next_point[i];
forward[i].next_point[i] = node;
}
}
public boolean erase(int num) {
Node[] forward = new Node[curLevel];
Node temp = head;
for (int i = curLevel - 1; i >= 0; i--) {
while (temp.next_point[i] != null && temp.next_point[i].val < num)
temp = temp.next_point[i];
forward[i] = temp;
}
boolean res = false;
if (temp.next_point[0] != null && temp.next_point[0].val == num) {
res = true;
// 更新连接
for (int i = curLevel - 1; i >= 0; i--)
if (forward[i].next_point[i] != null && forward[i].next_point[i].val == num)
forward[i].next_point[i] = forward[i].next_point[i].next_point[i];
}
// 删除孤立节点层
while (curLevel > 1 && head.next_point[curLevel - 1] == null)
curLevel -= 1;
return res;
}
public int randomLevel(double p) {
int level = 1;
while (Math.random() < p && level < MAX_LEVEL)
level++;
return level;
}
}
class Node {
int val;
Node[] next_point;
public Node(int val) {
this.val = val;
}
}
