确定问卷调查样本量
目录
- 1. 问卷数据类型
- 1.1 定性数据&定性分析
- 1.2 定量数据&定量分析
- 2. 确定初始样本容量:
- 2.1 公式:
- 2.2 Z值
- 2.3 p
- 2.4 e
- 2.5 举例
- 3.调整初始样本容量:
- 3.1 公式:
- 3.2 结论就是
- 小结:
1. 问卷数据类型
问卷时,可以根据研究目标和问题类型巧妙地结合定性和定量元素,以满足多样化的研究需求。
问卷数据类型分为定性数据和定量数据
1.1 定性数据&定性分析
定性数据常为文字数据,开放式的问题中询问调查对象的经历、感受、观点和信念等(除了问卷,一般调查方法还有:访谈、焦点小组、案例研究、文献综述等等。)
目的:细致的研究调查对象对有争议的、敏感的问题具体和独特的看法,发现关联性,可以补充定量数据,让研究者对调查的现象有更具体、完整的理解。
没有任何电脑软件能高质量地自动分析定性数据,研究者必须在不同的程度上人工归纳主题。
定性研究侧重于探讨观点并形成一种理论和假说,通过总结、分类和解释来分析,主要用文字来表达,需要调查的人群基数很小。
1.2 定量数据&定量分析
收集到的数据可量化,可以针对不同变量类型和研究问题来选择统计分析方法,
定量研究侧重于理论和假说,通过统计学和数学方法来分析,主要用数字和图表来表达,需要调查的人群基数很大。
量表属于定量调查
2. 确定初始样本容量:
针对样本量,统计上没有明确的要求多少,通常样本量在题目的5~10倍左右为宜。如果只是定性收集信息,问卷量没有标准多多益善,如果涉及定量调研需要考虑到样本量。
如果要根据样本推断总体就更复杂些。最直观的感觉是:样本量越大,误差就越小,但样本越大成本越高,所以在保证误差范围和可信度的情况下,我们可以根据公式计算出最小样本量:
前提是问卷采用随机抽样的方式发放,既:研究总体中每个个体都有相同的机会回答问卷。如果不是随机抽样,即使达到最小样本量也不可以进行推断统计,在朋友圈里或论坛里发的调研不是随机抽样不能做推断统计
2.1 公式:
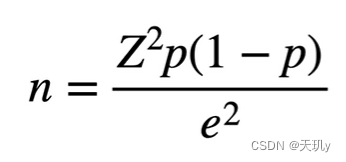
n:抽取的样本量
Z:Z值
p:指标比例
e:精度
2.2 Z值
置信度和Z值的对应关系:
| 置信度 | Z值 |
|---|---|
| 90% | 1.645 |
| 95% | 1.960 |
| 99% | 2.576 |
通常取95%
2.3 p
当p为0.5时求得的p(1-p)最大,也就是说需要样本容量最大
2.4 e
即是调查允许的误差范围
2.5 举例

3.调整初始样本容量:
首先要知道总体容量
3.1 公式:
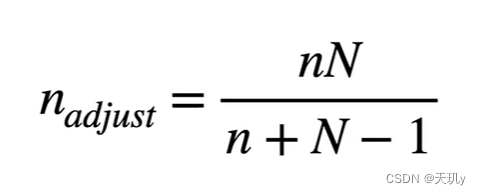
n:调整后抽取的样本量
N:总体容量
n_adjust:抽取的样本量
3.2 结论就是
需要在总体容量为N的总体中,至少随机得到n_adjust份有效问卷才能得出可靠结论,且误差在e以内。
小结:
关注我给大家分享更多有趣的知识,以下是个人公众号,提供 ||代码兼职|| ||代码问题求解||
由于本号流量还不足以发表推广,搜我的公众号即可: