交通 | 共乘出行（下）：基于图结构的动态多时空供需网络的均衡度量方法

博客：Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2

论文：Chin, Alex, and Zhiwei Qin. “A Unified Representation Framework for Rideshare Marketplace Equilibrium and Efficiency.” SIGSPATIAL 2023 (2023).

推文作者：郭王懿，陈泰劼，张云天

编者按：

共乘出行极大地改变了人们的日常出行方式。如何高效运营背后的双边平台是极具挑战性的工作。滴滴出行、Lyft公司是其中的佼佼者。本专题将探讨双边平台运营中的一个关键问题：如何科学度量双边平台的运营效率？

本专题分为上下两篇，递进推出。其中，上篇围绕滴滴出行、上海财经大学发表在统计学“四大”期刊之一《Journal of the American Statistical Association》的一篇文章 [1] 展开（https://mp.weixin.qq.com/s/kfMGWrqXwEmhzOLuG9nxVw）；下篇关注解读Lyft公司的一篇优质技术博客 [2] 和SIGSPATIAL 2023录用的一篇论文 [3]（https://sigspatial2023.sigspatial.org/）。

[1] Zhou, F., Luo, S., Qie, X., Ye, J., & Zhu, H. (2021). Graph-based equilibrium metrics for dynamic supply–demand systems with applications to ride-sourcing platforms. Journal of the American Statistical Association, 116(536), 1688-1699.

[2] Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2

[3] Chin, Alex, and Zhiwei Qin. “A Unified Representation Framework for Rideshare Marketplace Equilibrium and Efficiency.” SIGSPATIAL 2023 (2023).

引言

通常共乘出行的供需市场健康取决于乘客和司机的时空分布，但是在时空分布较为复杂的双边平台中，我们很难定义“市场效率”和“供需平衡”。比如，“我们有足够的司机吗？”可以有很多种理解方式：

• 在当前地点下是否有足够的司机来保证服务质量？
• 在整个系统中是否有足够的司机可以满足任意地点的乘客订单？
• 是否有足够的收入来维持司机的收益率？

为了更好的描述市场状态，我们必须研究监测市场状态的指标或方法。本文主要关注以下三个主要的问题：

1. 指标过多难以选择：现有的市场运行指标非常繁多，有乘客方面的指标包括取消率、预计到达时间、履约率等，司机方面的指标有司机在线时长，司机服务率（时间利用率）和收入等，平台方面的指标有乘车数量、财务指标等。同时监控大量指标是非常困难的，很难找到侧重点；并且这些指标通常容易受到外部变化（交通、天气、机场延误）的冲击影响。
2. 缺乏决策输出：指标的变化无法指导下一步的最佳决策，平台有很多工具可以改善市场状况，包括定价、调度、激励政策等，但是需要决策如何进行市场调整。
3. 指标信息冗杂：包含大量噪音的指标表示的信息通常非常复杂， 分析师很难从指标中掌握核心发生的事情。此外这些指标的单位通常异构，因此协调不同指标的方法并不直观。

目前共乘出行双边市场迫切需要一个供需状态的简洁表示方法，同时需要一个共乘出行市场效率的表征方法和数值测试。本文提出了一个基于GEM的供需时空状态度量方法和双边市场效率评估统一框架。

一、基于图结构的均衡度量方法(GEM)回顾

我们在 共乘出行（上）中详细介绍了GEM框架。

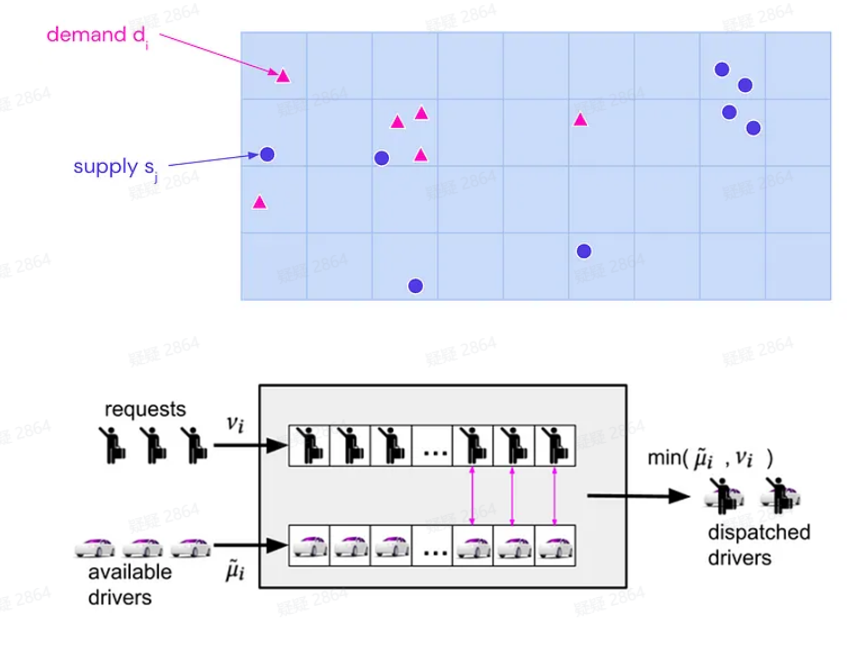
这里我们同样将城市划分为$N$个区域，构建图$G=(\mathbb{V},\mathbb{E})$，其中$v\in \mathbb{V}$分别代表$N$个节点，$|\mathbb{V}|=N$，每个边$e_{ij}=(vi, vj)∈ \mathbb{E} $都有一个对应的运输成本$w_{ij}$，代表从$i$区域转移到$j$区域需要的成本。从图$G$和权重矩阵$W=(w_{ij})$可以定义两种额外的属性：邻居节点$N_i$和成本矩阵$C =(c_{ij})$。邻居节点$N_i$是与节点$i$直接相连的节点集合，成本矩阵定义为$c_{i j}=\inf_{\text {paths } p} \sum_{(k, \ell) \in p} w_{k \ell}$，用于描述节点之间的最小转移成本。每个节点都有对应的供应和需求数目分别用测度$\mu$和测度$\nu$表示，比如$\mu_i$就表示节点$i$中可供调度的司机的数量，$\nu_i$就表示节点$i$中呼叫司机的乘客的数量。

1. GEM优化问题

根据上述定义，下面回顾一下GEM优化问题，GEM定义的优化问题由供需不匹配程度和转移成本两部分构成，同时需要满足供需平衡的调度约束：
$$\begin{array}{c}{\rho }_{\lambda }(\mu ,v)=\underset{\gamma \in \Gamma }{\min }\left\{\Vert v-\tilde{\mu }{\Vert }_1+\lambda \sum _{v_i\in \mathcal{V}}\sum _{v_j\in \mathcal{V}}{c}_{ij}{\gamma }_{ij}\right\}\\ s.t.\sum _{v_j\in {\mathcal{N}}_i}{\gamma }_{ij}={\mu }_i,\sum _{v_j\notin {\mathcal{N}}_i}{\gamma }_{ij}=0,{\tilde{\mu }}_i=\sum _{v_i\in {\mathcal{N}}_j}{\gamma }_{ji},\text{ for all }{v}_i\in \mathcal{V}.\end{array}$$
其中的决策变量是转移策略矩阵$({\gamma }_{ij})$，其含义是将接单司机从区域i调配到区域j的数量，$\tilde{\mu }$是$\mu$经过策略转移后的最优分布。$\tilde{\mu }$相比于$\mu$可以更真实的反应供应质量，因为调度后的结果可以考虑到每个司机的调度范围。目标函数${\rho }_{\lambda }$所定义的距离是一种广义的非对称距离。

2. 市场供需平衡状态度量方法

根据上述问题的求解结果，我们可以将局部供需平衡间隙（Local supply-demand gap）定义为$m_i=\log {\tilde{\mu }}_i-\log v_i$，当供应或需求为0时会用一个极小的正数代替。由于这种定义方法既是一种加性度量，又与市场的规模无关，所以在实际表现中比以往的${\mathrm{DSr}}_i=v_i/\max \left({\tilde{\mu }}_i,1\right)$和${\mathrm{DSd}}_i=v_i-{\tilde{\mu }}_i$表现效果好。

逐时计算局部供需平衡间隙后，可以得到一组矩阵$(m_{i,t})$，将其聚合后可以得到市场视角下的全局供需平衡间隙:
$$A_d=\frac{{\sum }_{i,t}{m}_{i,t}{v}_{i,t}}{{\sum }_{i,t}{v}_{i,t}}={\mathbb{E}}_{(i,t)\sim v}\left[m_{i,t}\right]$$
如果全局供需平衡间隙$A_d$是正数，则目前市场处于供大于求状态，负值则意味着供不应求。该表达式的含义为局部供需平衡间隙对需求的加权平均，是一种以需求为中心视角的市场平衡状态。代表随机选择一个打车用户看到的市场的状态，并解答了问题1：“在当前地点下是否有足够的司机来保证服务质量？”。

3. 基于GEM对偶问题的市场供需状态诊断

基于GEM优化问题的求解结果定义向量 γ ~ : = { γ i j , j ∈ N i } ∈ R N 0 \tilde{\gamma}:=\left\{\gamma_{i j}, j \in \mathcal{N}_i\right\} \in \mathbb{R}^{N_0} γ~​:={γij​,j∈Ni​}∈RN0​，其中${\mathcal{N}}_i$是节点i的相邻节点，$N_0=\sum_1^N n_i $是所有节点相邻节点数目之和，$\tilde{c} \in \mathbb{R}^{N_0}$是转移成本的向量形式。GEM定义可以写为LP形式：
$$\begin{array}{rl}\underset{\tilde{\gamma }\ge 0,s\ge 0}{\min }& 1^{T}s+\lambda {\tilde{c}}^T\tilde{\gamma }\\ \text{ s.t. }& A_1\tilde{\gamma }=\mu ,\\ & A_2\tilde{\gamma }+s\ge v,\\ & A_2\tilde{\gamma }-s\le v,.\end{array}$$
后两个约束用于线性化原GEM定义中的$L_1$正则形式，我们将三个约束的对偶变量分别定义为$w,u^u,u^o$,从约束的不等号可以得出$u^u\ge 0,u^o\le 0$。根据互补松弛条件，如果给定时空位置$(i,t)$并求解上述线性规划问题后，${\left(A_2\tilde{\gamma }\right)}_{i,t}>v_{i,t}$,则$u_{i,t}^u=0$,如果${\left(A_2\tilde{\gamma }\right)}_{i,t}<v_{i,t}$则$u_{i,t}^o=0$，因此定义$u:=u^u+u^o$来定义新增一个订单需求对GEM目标函数的边际影响（Marginal effect）。这里的对偶值代表的是整个系统的供需平衡差距以及应对扰动的运输成本。需求约束对偶$u_{i,t}$可以为需求转移策略提供初步的策略。如果$u_{i,t}$在特定时间特定节点为负值，说明需求可以适当增加来降低目标函数，反之如果$u_{i,t}$为正，则降低需求可以更好的实现市场平衡。供应约束对偶$w_{i,t}$代表为$(i,t)$增加一个司机后对目标函数的影响，该对偶值可以最需要司机的地方，从而为调度提供指导。下图则清晰的表明了对偶值可以对区域的司机调度提供帮助，订单多的地方最需要司机。

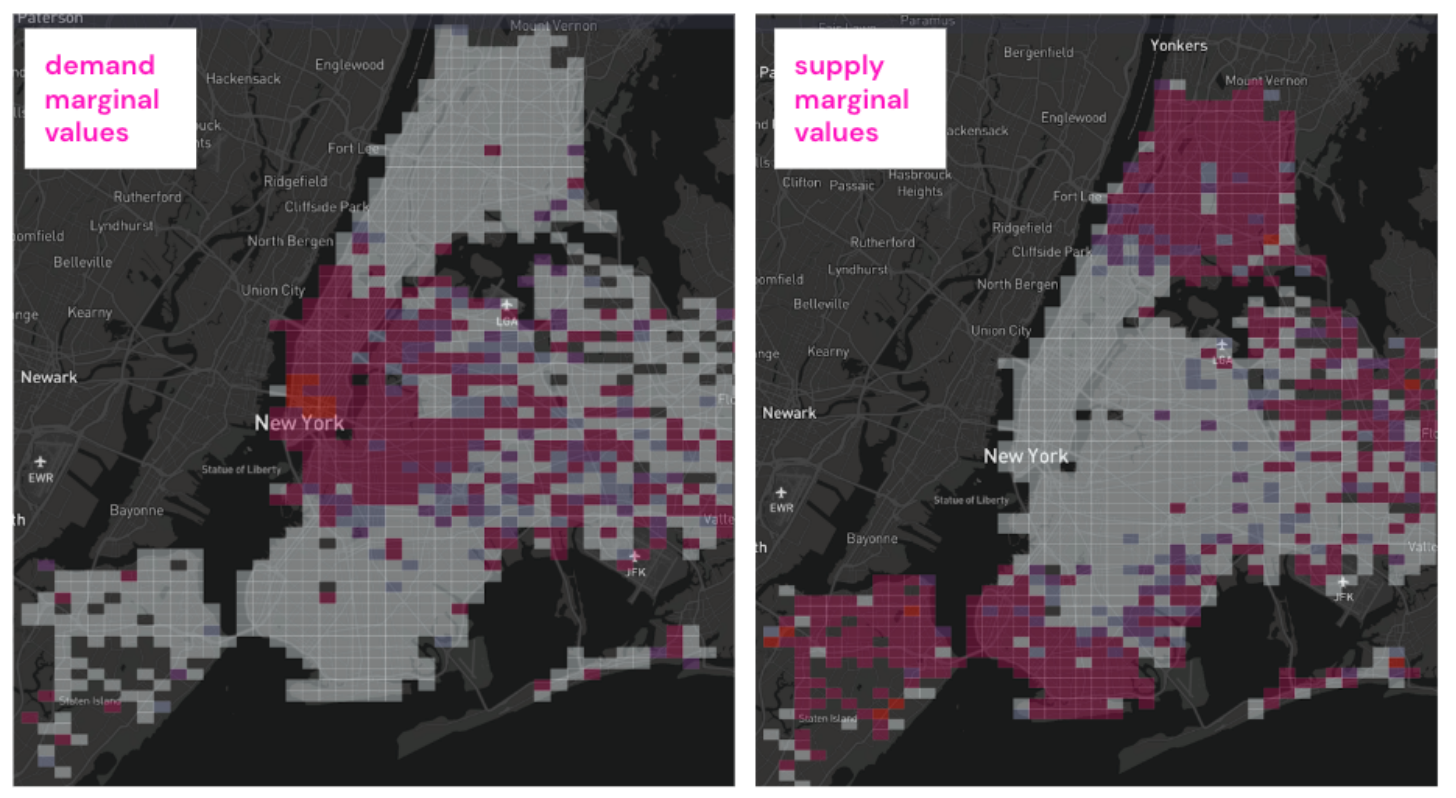
GEM对偶值在某一历史数据上的分布，红色：更大（正）的对偶值，浅色：更小（负）的对偶值

二、供需市场的双边视角

为了在供需两侧视角上获得更全面的市场画像，本文在原GEM基础上构造SD-GEM，并且构造了从供需双边视角上度量市场状态变化对市场效率的影响。

1. 供应侧视角和需求侧视角

在SD-GEM中，我们在上文提到的供应侧视角的基础上补充了需求侧视角下的市场均衡度：
$$A_s=\frac{{\sum }_{i,t}{m}_{i,t}{\tilde{\mu }}_{i,t}}{{\sum }_{i,t}{\tilde{\mu }}_{i,t}}={\mathbb{E}}_{(i,t)\sim \tilde{\mu }}\left[m_{i,t}\right]$$
相比于$A_d$，$A_s$在供应集中的区域SD gap的权重相对较大。其含义是在随机一个司机的视角下的本地市场均衡状态。正值过高的$A_s$意味着越来越多司机要争抢有限的订单资源，因此会导致较低的车辆利用率和回报率。

2. 供需平衡双边视角的案例诠释

我们用一个调度案例来解释上面提到的双边视角，图中的粉色圆形代表司机，蓝色三角形代表乘客订单，整个区域被分为了四部分。每个司机只能匹配当前区域和相邻区域的乘客，黑色箭头代表间接匹配。算例中$ϵ=0.5$。

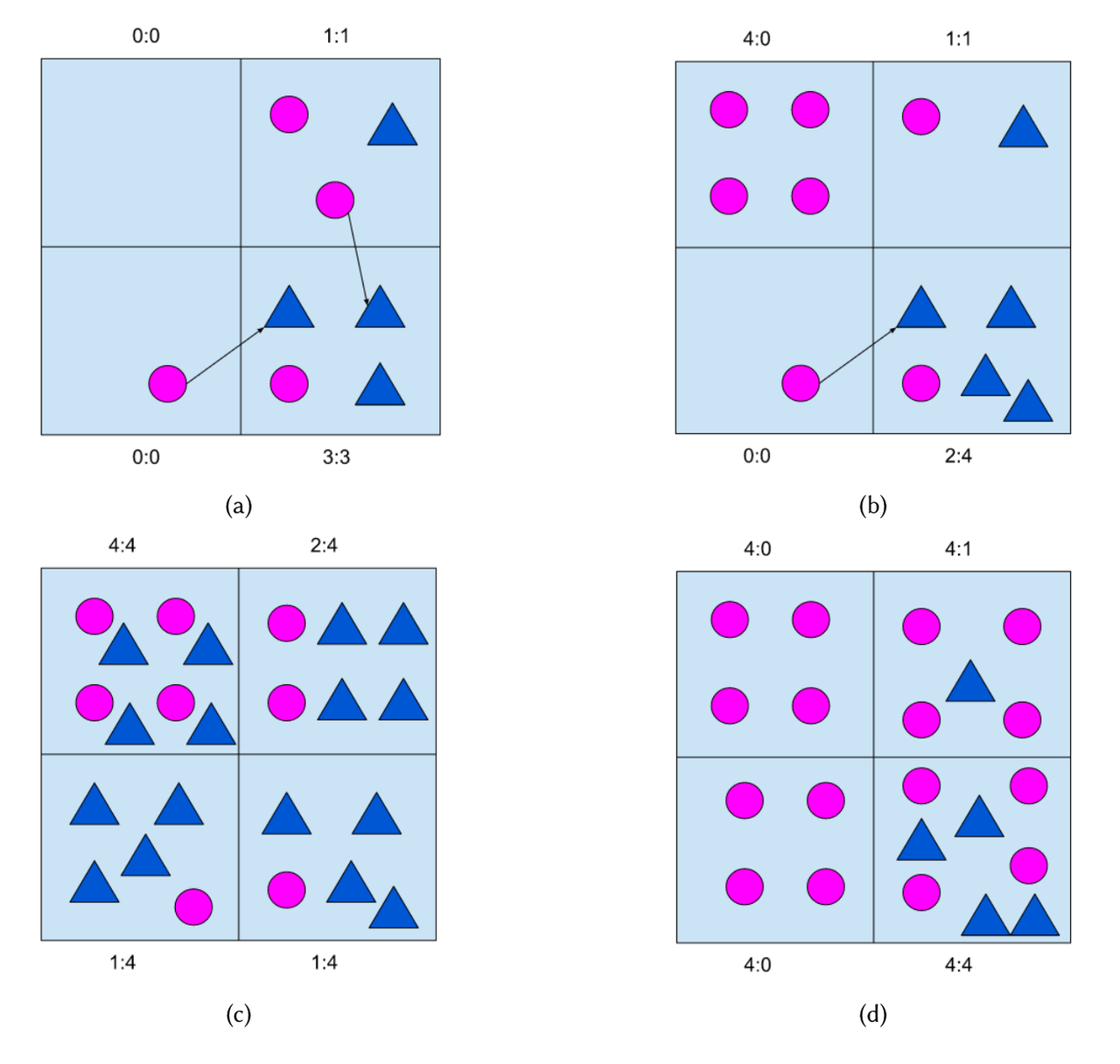
双边视角下的供需平衡视图

全局平衡案例：图a表示司机和乘客视角均为平衡状态$A_d=0,A_s=0$，是一种理想的状态；
供需偏差案例：图b表示乘客是一种供不应求的状态，司机是供大于求的状态，$A_d=-0.24,A_s=1.05$。SD-GEM的双边视角结论是相反的，这说明了有的司机不在最佳的位置上，因此我们可以通过司机调度来更好的实现市场平衡。
整体供不应求：图c描述的是整体供不应求的情况，$A_d=-0.87,A_s=-0.52$，这种情况下对司机的保留和获取非常关键。
整体供大于求：图d描述整体供大于求的状态，$A_d=0.28,A_s=1.39$，需求订单采集和供应控制较为关键。

3. 供需平衡双边平台的时间排队论视角

为了更好的理解双边视角下均衡度的测量意义，我们现从排队论的视角来看每个区域单元的双边均衡度。在任意时间窗口内，需求流入由上一时间窗口未丢弃的请求和当前窗口的新请求构成，需求流出由已经匹配的订单和取消的订单组成；司机流入由新登录司机和上一时间窗口未匹配司机构成，司机流出由匹配订单的司机和登出司机组成。

我们假设订单匹配中乘客和司机是一对一的，并且乘客取消和司机登出均发生在订单匹配好之前，输入输出流中的任何不匹配均保留到下一个时间窗。在这个一对一匹配机制下，每个时空单元下只能积累供应或需求中的一种，但在不同的单元内可以积累司机或乘客订单，上述GEM定义就是每个单元中不匹配度的权和。

当考虑到包含多个供需队列的区域级系统时，系统的供需分布复杂性受到内部机理影响。由于在指定时间内到达指定位置的司机收到先前需求订单的影响，因此需求模式对系统时空供需状态有影响。因此在双边平台中对供需分配进行何种程度的干预仍然是一个热门问题。

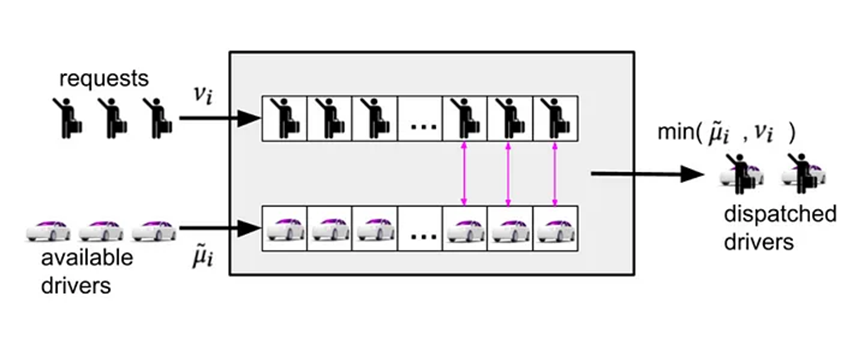
单个时空单元下的供需队列

三、SD-GEM在双边平台的应用

SD-GEM的指标$(A_d,A_s)$提供了一种度量市场效率的工具，直观地来说就是为了为了维持需求视角市场平衡的指标$A_d$，供应视角市场平衡指标就至少是$A_s$。$(0,0)$是最理想的市场平衡状态，因为需求视角和供应视角下都没有出现不平衡，因此越接近$(0,0)$市场效率就越高。

1. 单个区域的双边市场状态转移描述

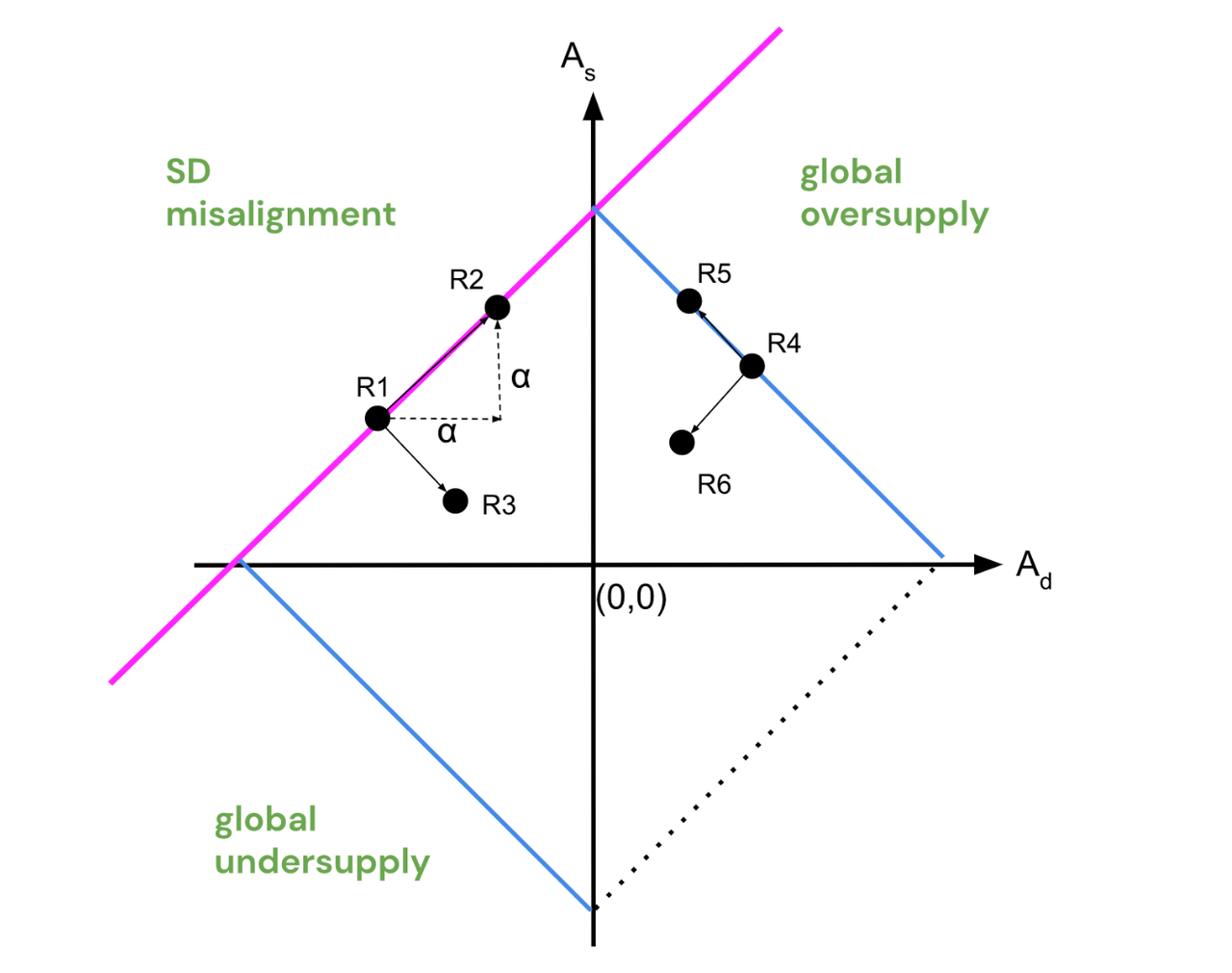
为了展示SD-GEM视角下市场状态转移，我们假设一种供应激增的状态。我们假设市场中按照现有分布$\tilde{\mu }$新增了一部分司机，因此每个单元内司机按照比例$\beta$新增，所以$A_d,A_s$都会增加一个常数$\alpha =\log (1+\beta )$，在下图中为$R_1$沿着粉色直线转移到$R_2$。

供需双边视角下市场状态的转移

从数据指标角度来说，供应激增后的$A_d,A_s$为：
$$
A_d^{\prime}=\frac{\sum_{i, t}\left(m_{i, t}+\alpha\right) v_{i, t}}{\sum_{i, t} v_{i, t}}=A_d+\alpha
\
A_s^{\prime}=\frac{\sum_{i, t}\left(m_{i, t}+\alpha\right) \tilde{\mu}^{\prime}{ }{i, t}}{\sum{i, t} \tilde{\mu}{i, t}^{\prime}}=\frac{\sum{i, t} m_{i, t} \tilde{\mu}^{\prime}{ }{i, t}}{\tilde{\mu}{i, t}^{\prime}}+\alpha

$$
其中$\widetilde{{\mu }^{\prime }}$是经过GEM计算后的供应激增后最优供应调度分布。按照假设可以得到${\widetilde{{\mu }^{\prime }}}_{i,t}={\tilde{\mu }}_{i,t}(1+\beta )$。同样如果订单需求按照现有分布激增一定比例，有相同的参数$\alpha ,\beta$。因此如果在不改变现有供需分布的前提下改变需求或供应，市场状态会沿着图中的粉色直线移动。这种移动通常是市场自行发展产生的移动。

在第二象限中还有一种移动方式是$R_1$到$R_3$，代表帕累托意义下的提升，通常需要激励性的政策来讲供需分布调整到全局最优的分布。在图中四个象限分别的供需状态含义如下表所示：

供需状态关系对应表

在第二象限中通过激励政策沿垂直粉色直线的方向移动很有意义，即激励性的政策较有意义。在一三象限中，沿粉色直线方向移动（$R_4$移动到$R_6$）是最快的提升市场效率的方法。然而沿着垂直粉色直线的方向反而没有意义。直观地来说，在全局供大于求或供不应求的情况下，寻求新的司机或者订单比调整供需分布更重要。

2. 城市级的双边市场画像刻画

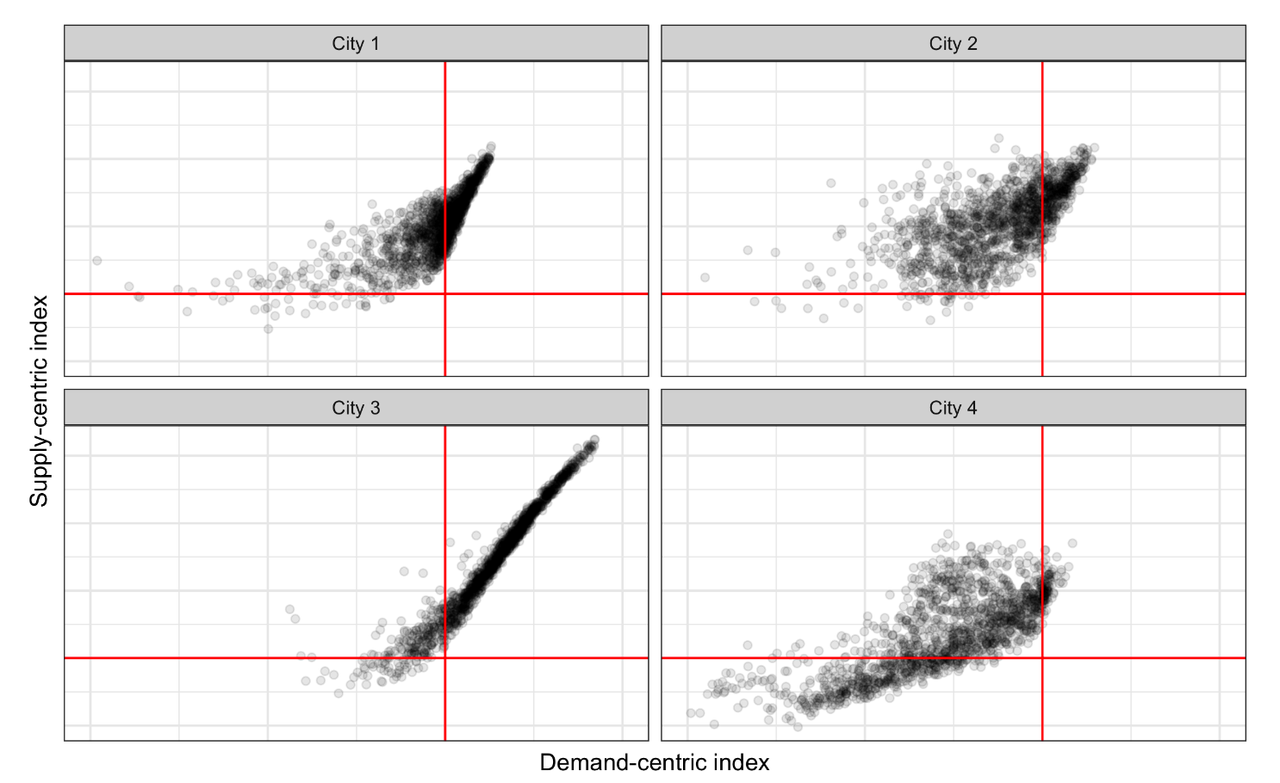
下图展示的是双边视角下城市级的数据图。可以看到在需求侧的负象限斜率稍微平缓，直观的解释是当$A_d$为负值供不应求的时候，额外的供应更容易被匹配。当$A_d$为正数，额外的供应会导致供大于求。同时从图中可以发现，不同城市的道路拓扑结构对供需散点图的覆盖形状影响很大。城市2是有少量主干道的细长形状的城市，由于司机的分布需要主动匹配需求的分布，在新增需求后司机的匹配度波动非常大。城市3是典型的密集市区，区域之间道路连接充分，高度互联互通，因此供需匹配非常容易，所以点图波动性较小。

在SD-GEM双边视角下的多个城市画像

四、小结

与标准的度量指标相比，SD-GEM框架有如下优势：

1. 提供供应侧和需求侧视角下的统一度量指标，分析权衡的时候容易。
2. 同时度量了市场均衡度和市场效率。
3. 展示了匹配和调度层面的直接数据，数据质量受混淆和突发的影响较少。

SD-GEM为市场效率和平衡度量开发一个创新的框架，帮助我们解决了本文开头提到的一些挑战:大量指标中难以选择，缺乏可操作的输出，以及混杂的信息。

参考文献

[1] Zhou, F., Luo, S., Qie, X., Ye, J., & Zhu, H. (2021). Graph-based equilibrium metrics for dynamic supply–demand systems with applications to ride-sourcing platforms. Journal of the American Statistical Association, 116(536), 1688-1699.

[2] Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2

[3] Chin, Alex, and Zhiwei Qin. “A Unified Representation Framework for Rideshare Marketplace Equilibrium and Efficiency.” SIGSPATIAL 2023 (2023).